Pravilni polieder
Pravilni poliedri so poliedri, ki imajo skladna vsa oglišča, stranice in stranske ploskve. Definicij za pravilne poliedre je več, najstrožje dovoljujejo le 5 pravilnih poliedrov (Platonska telesa), medtem ko najbolj obširne dovoljujejo neskončno mnogo pravilnih poliedrov. Dandanes je najbolj popularna definicija, ki dovoljuje 9 pravilnih poliedrov, ter številne razširjene definicije, najbolj popularna dovoljuje 48 pravilnih poliedrov. Prve omembe poliedrov segajo že v 4. stoletje pred našim štetjem, ko je Platon opisal Platonska telesa. Kasneje je še Johannes Kepler odkril 2, katerima je nato v 19. stoletju našel duale Louis Pointsot. V dvajsetem stoletju so nato začeli iskati različne neskončne poliedre, katerih običajno ne vključimo v navadno definicijo pravilnih poliedrov.
Petrialni poliedri zaključenih pravilnih poliedrov so prav tako zaključeni, vendar običajno niso vključeni v strožje definicije, saj njihove stranske ploskve niso vključene v strožjo definicijo pravilnih mnogokotnikov. Ti imajo namreč stranske ploskve razporejene po tridimenzionalnem prostoru, temu rečemo, da so izkrivljene. Ti mnogokotniki imajo še vedno enako dolge stranice, vendar te ležijo na različnih ravninah.
Neskončni pravilni poliedri (pravilni apeiroedri) so različna tlakovanja. Najbolj poznana so planarna tlakovanja, obstaja pa tudi nekaj pravilnih neplanarnih apeiroedrov, tako imenovani “blended” (mešani) apeiroedri. Ti zaradi nezaključnosti prav tako niso vključeni v strožje definicije pravilnih poliedrov.
Pravilni poliedri do sedaj so vsi ”pravilni” v trorazsežnem evklidskem prostoru, poznamo pa tudi neskončno mnogo pravilnih poliedrov v sferičnem in hiperboličnem prostoru. Obstajajo tudi abstraktni poliedri, to so trorazsežna telesa, ki so pravilna le v več kot trirazsežnem prostoru.
Poliedre največkrat delimo po odkriteljih (Platonska telesa, Keplerjeva telesa …), obstajajo pa tudi druge delitve.
Definicije[uredi | uredi kodo]
Obstaja veliko različnih definicij, ki dovoljujejo različno število pravilnih poliedrov. Vse definicije imajo naslednje omejitve:
- vsi diederski koti poliedra morajo biti enaki
- vse slike oglišč so pravilni mnogokotniki (pri definicijah, ki zajemajo več poliedrov se štejejo tudi pravilni izkrivljeni mnogokotniki)
- vse stranice, oglišča in stranske ploskve so skladne.
Petrie-Coxeterjeva definicija[uredi | uredi kodo]
Prva definicija Petrieja in Coxeterja je dovoljevala vse pravilne poliedre, ki so v 3D evklidskem prostoru s tem omejila pravilne poliedre na 48 različnih. S to definicijo jima je uspelo najti šest novih pravilnih poliedrov, ki predstavljajo osnovo za kasneje odkritih šest, ki tudi spadajo v definicijo. Ta definicija še vedno dovoljuje neskončno velike pravilne poliedre, ki jih nadaljnje definicije ne dovoljujejo več.[1]
Definicija, ki omejuje zaključenost pravilnega poliedra[uredi | uredi kodo]
Ta definicija za razliko od Petrie-Coxeterjeve definicije dovoljuje pravilne poliedre izven evklidskega prostora, vendar morajo biti poliedri zaključeni. Ta definicija ne dovoljuje tlakovanj, vendar dovoljuje še vedno neskončno mnogo pravilnih poliedrov. Definicija nima pravega imena in se bolj redko uporablja.
Standardna definicija[uredi | uredi kodo]
To je največkrat uporabljena definicija in se običajno uporablja pri opisovanju pravilnih poliedrov. Definicija dovoljuje le zaključene pravilne poliedre znotraj 3D evklidskega prostora ter tako omejuje število na 9 pravilnih poliedrov, na platonska ter Kepler-Pointsotova telesa.
Schläflijeva definicija[uredi | uredi kodo]
Ludwig Schläflij je zagovarjal, da morajo imeti vsi pravilni poliedri Eulerjevo karakteristiko 2, to pa imajo le platonska ter veliki zvezdni dodekaeder in veliki ikozaeder. Čeprav on sam ni štel niti Keplerjevih teles pod pravilne poliedre, so ti dovoljeni v tej definiciji.
Osnovnošolska definicija[uredi | uredi kodo]
To definicijo se zaradi omejitve teles le na najpreprostejša pogosto uporablja v osnovnih šolah, vsekakor pa se ne pojavlja le tam. Definicija zahteva, da so pravilni poliedri zaključeni, so v evklidskem 3D prostoru ter so konveksni. S tem smo omejili pravilne poliedre le na 5 platonskih teles. Ta definicija se pogosto uporablja tudi med ljudmi, ki nimajo poglobljenega znanja v matematiki. Definicijo so uporabljali tudi stari Grki, saj še niso poznali drugih pravilnih poliedrov.
Označevanje[uredi | uredi kodo]
Za pravilne politope se najpogosteje uporablja označevanje s Schläflijevim simbolom. V treh dimenzijah mora imeti dve števili, ki se na splošno označita s p in q, torej Schläflijev simbol za nek polieder je {p, q}. V simbolu p predstavlja kateri mnogokotnik sestavlja pravilni polieder – polieder je torej iz p-kotnikov. Število q pa predstavlja koliko stranskih ploskev se stika v enem oglišču. Simbol {4, 3} torej pomeni, da je polieder sestavljen iz pravilnih štirikotnikov (kvadratov) in da se v vsakem oglišču stikajo trije kvadrati. Vendar se označevanje že pri standardni definiciji mora spremeniti, saj drugače bi prišlo do različnih poliedrov označenih enako. Problem predstavlja pentagram, saj je kot konveksni petkotnik, prav tako petkotnik. Za pentagram in dekagram se zato uporablja oznaka {p, qn}, kjer n predstvlja stopnjo stelacije. Nekateri petriali imajo prav tako enak Schläflijev simbol kot nekatera druga telesa, zato se pri njih poleg osnovnega simbola na koncu napiše še število mnogokotnika, ki je stranska ploskev petrialnega para, npr. Schläflijev simbol za petrialno kocko je {6, 3}4. To pomeni, da ima petrialna kocka za stranske ploskve šestkotnike in da se po trije stikajo na enem oglišču. Če bi zapisali samo {6, 3}, petrialne kocke ne bi bilo mogoče razločiti od šestkotnega tlakovanja, zato na koncu podpišemo še 4, saj ima petrialni par (navadna kocka) za osnovno ploskev pravilne štirikotnike (kvadrate). Pri petrialih se uporablja tudi zapis s simbolom petrialnega para in na koncu nadčrtamo π, npr. {4, 3}π. Pri Petrie-Coxeterjevih poliedrih je potrebno tudi napisati obliko lukenj, ki nastopajo med stranskimi ploskvami. Splošen simbol je {p1, q|p2}. Število p1 predstavlja p-kotnik stranske ploskve, p2 pa p-kotnik luknje med stranskimi ploskvami. Naslednja posebnost je pri “blended” apeiroedrih, saj moramo nakazati ali “blendamo” s segmentom ali z apeiroedrom. Prav tako p in q nista od stranske ploskve, temveč od stranske ploskve tlakovanja iz katerega izhaja. Posebnost zase je še izkrivljeni muoktaeder, katerega zapis je {∞, 4}·,∗3, kjer∗ stoji pred številom, ki predstavlja obliko luknje ali cikcaka dualnega para. S · smo zamenjali ∞ da nakažemo, da je vrednost nedoločena.[2]
Platonska telesa[uredi | uredi kodo]

Najbolj poznani pravilni poliedri so platonska telesa, ter so edini poliedri, ki upoštevajo vse definicije. Platonska telesa so osnova za vse zaključene poliedre v evklidskem 3D prostoru. Poznali so jih že v starih civilizacijah, prvi zapis o njih pa je nastal okoli leta 360 pred našim štetjem, ko jih je opisal Platon. Platonskih teles je pet, kot stranske ploskve pa imajo trikotnike, kvadrate ali petkotnike. Vsi so konveksni in zaključeni. Vsi imajo dualne pare (tetraeder je sam sebi dualni par) in petrialne pare. Glavne tri simetrije – tetraederska, oktaederska in ikozaederska – so poimenovane po platonskih telesih.
Platonskim telesom se lahko določi včrtane, vmesne in očrtane sfere. Vsa telesa imajo tudi eulerjevo karkteristiko 2.
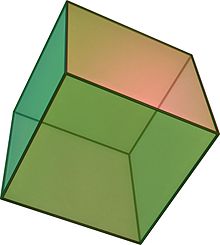
Tetraeder Heksaeder (kocka)
Oktaeder Dodekaeder Ikozaeder slika 




animacija 


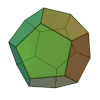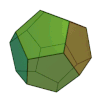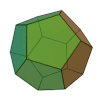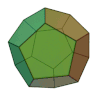

3D model 




mreža 




Schläflijev simbol {3, 3} {4, 3} {3, 4} {5, 3} {3, 5} osnovna ploskev trikotnik kvadrat trikotnik petkotnik trikotnik št. stranskih ploskev 4 6 8 12 20 št. oglišč 4 8 6 20 12 št. robov 6 12 12 30 30 simetrija tetraederska oktaederska oktaederska ikozaederska ikozaederska dual sam sebi oktaeder heksaeder ikozaeder dodekaeder
Dokazovanje platonskih teles[uredi | uredi kodo]
Da je le pet različnih platonskih teles lahko dokažemo na več načinov.
Geometrijski dokaz[uredi | uredi kodo]
Geometrijsko je dokazal že Evklid v svoji knjigi Elementi.
Da telo lahko obstaja mora imeti vsaj tri stranske ploskve, ki se stikajo v enem oglišču (q ≥ 3) ter za stransko ploskev enake pravilne mnogokotnike (p ≥ 3). V vsakem oglišču telesa mora biti med sosednjimi stranskimi ploskvami vsota kotov manjša od 360°, torej mora biti notranji kot mnogokotnika manjši od 360°3 = 120° (tri-, štiri- ali petkotnik, saj šestkotnik ima kot 120°). Razlika med 360° in vsotami kotov istega oglišča se imenuje kotni primanjkljaj.
Pri trikotnikih imamo tri možne poliedre, saj se lahko na istem oglišču stikajo trije, štirje ali pet trikotnikov, ki tvorijo teraeder, oktaeder in ikozaeder. Šest jih že tvori kot 360° in tako tvorijo teselacijo in ne platonskega telesa. Pri kvadratih in petkotnikih je edina možnost s tremi liki na oglišče, saj štirje že tvorijo kot 360° oz. 432°. Mnogokotniki z več stranicami, kot 5 niso zmožni tvoriti platonskega telesa, saj če bi se trije stikali na istem oglišču kotnega primankljaja ne bi bilo ali bi bil kot večji od 360°.
| trije trikotniki | štirje trikotniki | pet trikotnikov | šest trikotnikov | trije kvadrati | štirje kvadrati | trije petkotniki | trije šestkotniki | |
| slika | 
|

|

|

|

|
|

|

|
| kot | 180° | 240° | 300° | 360° | 270° | 360° | 324° | 360° |
| primanjkljaj | 180° | 120° | 60° | 0° | 90° | 0° | 36° | 0° |
| telo | {3, 3}
tetraeder |
{3, 4}
oktaeder |
{3, 5}
ikozaeder |
Ø | {4, 3}
heksaeder |
Ø | {5, 3}
dodekaeder |
Ø |
V bistvu lahko le iz primankljaja ugotovimo število oglišč v platonskem telesu z uporabo Descartesovega izreka:
V enačbi V predstavlja število oglišč, q število mnogokotnikov okrog enega oglišča in α notranji kot enega mnogokotnika.
Topološki dokaz[uredi | uredi kodo]
Topološki izraz izhaja iz dejstva da je Eulerjeva karakteristika pri vseh platonskih telesih 2:
Za vsa platonska telesa velja tudi naslednja enačba:
Če enačbi združimo, dobimo naslednjo enačbo:
To enačbo se zlahka poenostavi v naslednjo:
Število robov (E) je lahko le pozitivno, saj ne moremo imeti negativno število robov. Iz tega lahko dobimo naslednjo neenačbo:
Ker morata biti p in q naravni števili, večji od 3, dobimo 5 rešitev, ki se ujemajo s platonskimi telesi.
Kepler-Poinsotovi poliedri[uredi | uredi kodo]
Keplerjeve poliedre ter Pointsotove poliedre velikokrat združimo pod skupnim imenom Kepler-Pointsotovi poliedri, saj so dualni pari.
Keplerjeva poliedra je okoli leta 1619 odkril Johannes Kepler. Kot osnovni ploskvi imata pentagram, torej nista konveksna. Po začetku znanstvenega klasificiranja poliedrov pa je Louis Poinsot leta 1806 odkril še njuna duala. Tudi duala nista konveksna, čeprav sta iz trikotnikov in petkotnikov – konveksnih mnogokotnikov. Značilnost Kepler-Poinsotovih poliedrov je tudi ikozaedrska simetrija. Keplerjevi telesi lahko dobimo tudi z procesom facetiranja oz. stelacije. S facetiranjem ikozaedra dobimo veliki dodekaeder, s facetiranjem malega zvezdenga dodekaedra pa veliki ikozaeder:
Mali zvezdni dodekaeder (mali stelirani dodekaeder)
Veliki dodekaeder Veliki zvezdni dodekaeder (veliki stelirani dodekaeder)
Veliki ikozaeder slika 



animacija 



3D model 



mreža (osnovne ploskve mreže niso osnovne ploskve,
saj v realnem svetu ne
moremo narediti
Kepler-Poitsotovih poliedrov
iz njihovih osnovnih ploskev,
saj se te med seboj sekajo)




×12
Schläflijev simbol {52, 5} {5, 52} {52, 3} {3, 52} osnovna ploskev pentagram petkotnik pentagram trikotnik št. stranskih ploskev 12 12 12 20 št. oglišč 12 12 20 12 št. robov 30 30 30 30 Eulerjeva karakteristika −6 −6 2 2 dual veliki dodekaeder mali stelirani dodekaeder veliki ikozaeder veliki stelirani dodekaeder
Dokazovanje Kepler-Poinsotovih teles[uredi | uredi kodo]
Leta 1810 je matematik Augustin-Louis Cauchy dokazal, da obstajajo le štirje Kepler-Pointsotovi poliedri, vendar je njegov dokaz težko razumljiv in zapleten. Spodaj je napisan dokaz, ki ga je iznašel Joseph Bertrand.
Za katerikoli končni set točk v prostoru obstaja konveksni polieder, ki ima oglišča na nekaterih izmed točk, ostale pa znotraj sebe (v svoji konveksni ogrinjači). V polieder lahko postavimo pravilni stelirani polieder tako, da so ogljišča enega hkrati tudi oglišča drugega. Ta sistem lahko kličemo P in lahko mu naredimo kopijo Q. Ker je stelarni polieder v P pravilni, lahko P obračamo ali zrcalimo tako, da katerokoli oglišče v od P gre na katerokoli oglišče v' od Q ter se pri tem vsa druga oglišča P ujemajo z oglišči Q. Tako mora biti P izogonalen (ogliščno prehoden) in konveksna ogrinjača uniformni polieder. To razporeditev v do v' lahko naredimo na najmanj tri načine, z ujemanjem vsake stranske ploskve, ki ima najmanj dve drugi skladni stranski ploskvi z najmanj trikratno simetrijo okrog vsakega oglišča, kar izključuje vsa telesa razen platonskih teles. Kepler-Pointsotova telesa lahko tako nastanejo le z facetiranjem platonskih teles.[3]
Tetraeder ne more biti facetiran, saj nima diagonal. Oktaeder prav tako ne more biti facetiran, saj njegove diagonale tvorijo le tri kvadrate, pravokotne eden na drugega, ki niso zmožni tvoriti poliedra. Heksaeder (kocka) ima premalo prostorskih diagonal, da bi lahko tvorila polieder, ploskovne diagonale pa naredijo stello octangulo, ki je poliedrski sestav. Ostaneta nam tako le še dodekaeder in ikozaeder. Ikozaeder se lahko facetira na 3 različne poliedre, ki imajo za osnovno ploskev enake pravilne mnogokotnike. Novonastali polieder je lahko sestavljen iz 12 petkonikov (veliki dodekaeder), 12 pentagramov (mali stelirani dodekaeder) ali 20 trikotnikov (veliki ikozaeder). Dodekaeder se lahko facetira v heksaederske in tetraederske sestave, vendar tudi v velikega steliranega dodekaedra. Ker ni več platonskih teles tudi Kepler-Poinsotovih teles ne more biti več.[3]
Značilnosti pravilnih poliedrov znotraj standardne definicije[uredi | uredi kodo]
Ekvivalentnosti[uredi | uredi kodo]
V pravilnem poliedru so vsa oglišča skladna, torej se mora na vseh ogliščih stikati enako število ploskev. Za oglišča velja tudi:
- vsa oglišča poliedra ležijo na sferi
- vsi diedrski koti poliedra so enaki
- vse slike oglišč poliedra so pravilni mnogokotniki
- vsi prostorski koti poliedra so skladni
Koncentrične sfere[uredi | uredi kodo]
Pravilni poliedri imajo tri sfere, ki si delijo središča:
- včrtana sfera je tangentna na vse ploskve
- vmesna sfera je tangentna na vse robove
- očrtana sfera je tangentna na vsa oglišča
Simetrija[uredi | uredi kodo]
Pravilni poliedri so med poliedri najbolj simetrični. Nahajajo se v treh simetrijskih grupah, ki imajo imena po platonskih telesih:
- tetraederska (tudi simetrija četverca) – Td
- oktaederska (tudi heksaederska ali simetrija osmerca) – Oh
- ikozaederska (tudi dodekaederska) – Ih
Eulerjeva karakteristika[uredi | uredi kodo]
Pet platonskih teles ter veliki zvezdni dodekaeder in veliki ikozaeder imajo Eulerjevo karakteristiko (χ) enako dva, kar pomeni, da je površina poliedra topološka 2-sfera. Mali zvezdni dodekaeder in veliki dodekaeder sta, kar se tiče Eulerjeve karakteristike posebna, saj je pri njima −6. Zaradi tega ju Ludwig Schläfli ni uvrščal med pravilne poliedre.
Notranje točke[uredi | uredi kodo]
Vsota razdalj od poljubne točke znotraj pravilnega poliedra do stranic je neodvisna od lege točke (to je razširitev Vivianovega izreka). Obratno ne velja celo za tetraedre.[4]
Razmerja med pravilnimi poliedri[uredi | uredi kodo]
Znotraj standardne definicije pravilnih polierov le tetraeder ni v razmerju z nobenim drugim pravilnim poliedrom, vendar pri razširjenih definicijah dobi svoj petrialni par. Heksaeder je v razmerju le z oktaedrom, ostalih šest teles pa je v razmerju med sabo. Razmerje med poliedri lahko obstaja le med poliedri z enako vrsto simetrije. Poznamo šest osnovnih razmerij med pravilnimi poliedri, od tega se pojavljata dva med platonskimi in Kepler-Ponsotovimi poliedri. Osnovna razmerja lahko poljubno združujemo skupaj, vendar ni nujno, da ima vsak polieder to razmerje s katerim drugim pravilnim poliedrom.
Dual[uredi | uredi kodo]


Dual nekega poliedra je tisto telo, ki nastane s prisekavanjem – če poliedru odrežemo oglišča na tak način, da so nastali mnogokotniki skladni in pravilni, ter da od vsake dosedanje stranske ploskve ostane le sredinska točka – tam, kjer je nastalo novo oglišče. Dualni razmerje se označi z grško črko δ[2]. Da sta dve telesi dualni par se zlahka vidi iz Schläflijevega simbola, saj sta p in q vrdnosti zamenjani, npr. {4, 3} je dualni par od {3, 4}
Dualni pari znotraj standardne definicije:
- heksaeder in oktaeder
- dodekaeder in ikozaeder
- mali zvezdni dodekaeder in veliki dodekaeder
- veliki zvezdni dodekaeder in veliki ikozaeder
- Tetraeder ima tudi dualni par, vendar sam s sabo
Stelirani/facetirani par[uredi | uredi kodo]
Par nastane s stelacijo ali fecetacijo nekega poliedra. Označi se s grško črko φ, zraven pa je podana še stopnja stelacije, npr. φ2, če je stopnja stelacije 2[2].
Stelirani/facetirani pari znotraj standardne definicije:
- ikozaeder in veliki dodekaeder – φ2
- mali zvezdni dodekaeder in veliki ikozaeder – φ2
Razmerja med poliedri zunaj standardne definicije[uredi | uredi kodo]
Teh razmerij ne najdemo med platonskimi in Kepler-Ponsotovimi poliedri, ampak med bolj kompleksnimi poliedri.
- petrialni par (π[2]) je med dvema telesoma z enako lego oglišč in robov, vendar z drugačnimi stranskimi ploskvami
- razpolovljeni par (η[2]) je med telesoma, kjer ima eno telo svoje robove po diagonalah stranskih ploskev dugega
- vijačni par (σ[2]) je med telesoma, kjer se pri enemu telesu osnovna ploskev v neko stran periodično ponavlja, pri drugem pa to ponavljanje nadomešča vijačnica v obliki izhodiščne osnovne ploskve.
- ”blended” trojica je med telesi, pri katerem je eden planarna teselacija, druga dva pa trodimenzionalna različica teselacije. “Blendamo“ lahko z apeiroedrom ali z segmentom ter tako dobimo dve različici “blended“ teselacije.
Pravilni poliedri zunaj standardne definicije[uredi | uredi kodo]
Petriali pravilnih poliedrov znotraj standardne definicije[uredi | uredi kodo]
Petrial poliedra je polieder, ki ima s svojim petrialnim parom skladna oglišča in robove, vendar ne stranskih ploskev. To lahko storimo le, če je osnovna ploskev enega izmed njih izkrivljena v tretjo dimenzijo. Osnovno ploskev petriala dobimo, če začnemo v nekem oglišču, nato pa izmenično levo-desno sledimo stranicam dokler ne pridemo do izhodiščnega oglišča. Dobimo sklenjen cikcak. Če cikcak pogledamo pod pravim kotom izgleda kot pravilni mnogokotnik z oglišči na isti ravnini. Tako poimenujemo cikcake po pravilnih mnogokotnikih, vendar ker imajo oglišča razporejena po 3D prostoru se imenujejo izkrivljeni pravilni mnogokotniki. Petriale z izkrivljenimi stranskimi ploskvami se označi kot {p, q}n, kjer n označuje število p petrialnega para. Ta zapis je obvezen le za petrialni tetraeder, heksaeder in oktaeder.
| Petrialni
tetraeder |
Petrialni
heksaeder |
Petrialni
oktaeder |
Petrialni
dodekaeder |
Petrialni
ikozaeder |
Petrialni mali
zvezdni dodekaeder |
Petrialni
veliki dodekaeder |
Petrialni veliki
zvezdni dodekaeder |
Petrialni
veliki ikozaeder | |
|---|---|---|---|---|---|---|---|---|---|
| slika | 
|

|

|

|

|

|

|

|

|
| animacija | 
|

|

|

|

|

|

|

|

|
| animacija
osnovne ploskve |

|

|

|

|

|

|

|

|

|
| osnovna ploskev | izkrivljen kvadrat | izkrivljen šestkotnik | izkrivljen desetkotnik | izkrivljen šestkotnik | izkrivljen dekagram | ||||
| Schläflijev simbol | {4, 3}3 | {6, 3}4 | {6, 4}3 | {10, 3} | {10, 5} | {6, 52} | {6, 5} | {103, 52} | {103, 3} |
| št. stranskih ploskev | 3 | 4 | 4 | 6 | 6 | 10 | 10 | 6 | 6 |
| št. oglišč | 4 | 8 | 6 | 20 | 12 | 12 | 12 | 12 | 20 |
| št. robov | 6 | 12 | 12 | 30 | 30 | 30 | 30 | 30 | 30 |
| Eulerjeva karakteristika | 1 | 0 | −2 | −4 | −12 | −8 | −8 | −12 | −4 |
Dokazovanje petrialov[uredi | uredi kodo]
Najprej bomo dokazali, da obstaja 18 pravilnih zaključenih poliedrov v . Ker so pravilni zaključeni poliedri tudi platonska telesa ter Kepler-Poinsotova telesa tako lahko obstaja 9 petrialov.
Naj bo pravilni polieder v in naj bo njegova simetrijska grupa. Lahko rečemo, da je ortogonalna grupa, tako, da ima center . Prva stvar, ki jo lahko opazimo je, da morata biti in ravnini. Najlažji način, kako to lahko opazimo je, da za prvotno oglišče od velja . Tako mora vsebovati premico, vendar morata biti in različna in nekomutativna. je tako lahko premica ali ravnina. Ne more biti le set točke {}, ki bi bila edina druga vrsta involucije v ortogonalni grupi v , saj bi bil tako centralen in bi bil komutativen z .
Če je premica, jo nadomestimo z ortogonalno ravnino . Kot ortogonalna simetrija, , tj. produkt s centralnim zrcaljenjem. je tako še vedno komutatvna z , vendar ne z . Če je ravnina, določimo, da je . Nato določimo za . Zatem definiramo . Tako je končna zrcalna grupa v , ki je tudi simetrijska grupa devetih klasičnih pravilnih ploedrov . V vsaki grupi poliedra lahko zamenjamo z ter tako dobimo novo končno ortogonalno grupo v , nastalo z involucijami. To doda na seznam še devet pravilnih poliedrov, torej vse skupaj 18.[2]
Pravilni apeiroedri[uredi | uredi kodo]
Pravilne apeiroedre šteje pod pravilne poliedre le Petrie-Coxeterjeva definicija. Pravilne apeiroedre delimo v dve veliki skupini – apeiroedri se namreč lahko širijo v neskončnost v dveh dimenzijah (teselacije) ali v treh (čisti pravilni apeiroedri in pravilni poševni apeiroedri (Petrie-Coxeterjevi apeiroedri). Čeprav se “blendane” teselacije z apeiroedrom širijo v tri dimenzije, jih še vedno uvrščamo v prvo skupino, saj izhajajo iz planarnih teselacij.
Pravilne teselacije[uredi | uredi kodo]
Poznamo šest planarnih teselacij (trikotno, kvadratno in šestkotno ter njihove petriale). Vsaka od njih je del svoje “blended” trojice, saj lahko vsako od njih “blendamo” na dva različna načina in tako dobimo še dve različni pravilni teselaciji. Tako poznamo 18 teselacij. “Blendanih” teselacij ne zapisujemo s Schläflijevim simbolom, ki bi nam povedal p-kotnik, ki je stranska ploskev in število mnogokotnikov, ki se v enem oglišču stika, ampak z Schläflijevim simbolom planarnega apeiroedra, iz katerega izhaja ter posebno končnico. Za “blendane” s segmentom je # {}, za “blendane” z apeiroedrom pa # {∞}, saj se širijo v neskončnost tudi po tretji dimenziji. “Blended” trojica je torej {4, 4}; {4, 4} # {} in {4, 4} # {∞}.[2]
Planarne teselacije[uredi | uredi kodo]
Osnovne tri planarne teselacije (tlakovanja) so trikotniška, kvadratna in šestkotna. Da je teselacija planarna, pomeni, da ima vsa oglišča na isti ravnini. teselacije se širijo po ravnini v neskončnost, torej imajo neskončno število stranskih ploskev, oglišč in robov. Vse imajo svoje petrialne pare:
| Trikotno tlakovanje | Kvadratno tlakovanje | Šestkotno tlakovanje | Petrialno
trikotno tlakovanje |
Petrialno
kvadratno tlakovanje |
Petrialno
šestkotno tlakovanje | |
|---|---|---|---|---|---|---|
| slika | 
|

|

|

|

|

|
| Schläflijev simbol | {3, 6} | {4, 4} | {6, 3} | {∞, 6}3 | {∞, 4}4 | {∞, 3}6 |
| osnovna ploskev | trikotnik | kvadrat | šestkotnik | nesklenjen cikcak (60°) | nesklenjen cikcak (90°) | nesklenjen cikcak (120°) |
| simetrija | šestkratna rotacijska | štirikratna rotacijska | trikratna rotacijska | šestkratna rotacijska | štirikratna rotacijska | trikratna rotacijska |
| dual | šestkotno tlakovanje | sam sebi | trikotno tlakovanje | / | ||
Dokazovanje planarnih teselacij[uredi | uredi kodo]
Podobno kot pri platonskih telesih lahko tudi tukaj dokažemo z geometrijskim ali topološkim dokazom. Pri geometrijskem dokazu sedaj ne sme biti kotnega primankljaja, vsota kotov mora biti točno 360°. Enako kot pri platonskih telesih morata tudi tukaj biti p in q ≥ 3, torej mora biti notranji kot mnogokotnika manjši ali enak 360°3 = 120°. Tako se lahko omejimo le na tri-, štiri-, pet- in šestkotnike.
| šest trikotnikov | štirje kavdrati | trije petkotniki | trije petkotniki | |
| slika | 
|

|

|

|
| kot | 360° | 360° | 324° | 360° |
| primanjkljaj | 0° | 0° | 36° | 0° |
| teselacija | {3, 6}
trikotna teselacija |
{4, 4}
kvadratna teselacija |
Ø | {6, 3}
šestkotna teselacija |
Topološki dokaz je povsem enak tistemu za dokazovanje platonskih teles, le da mora sedaj veljati .
Geometrijski in topološki dokaz sta lahka za razumevanje, vendar ne dokažeta petrialov. Za dokaz da obstaja le šest planarnih teselacij moramo uporabiti splošni dokaz za dokazovanje pravilnih teselacij.
“Blended” teselacije[uredi | uredi kodo]
“Blended“ teselacije delimo na dve vrsti: “blended” teselacije s segmentom in “blended” teselacija z apeiroedrom.
“Blended” teselacije s segmentom nastanejo, ko oglišča periodnično premaknemo izven ravnine in puščamo v ravnini. Tako dobimo teselacijo, ki ima za stranske ploskve iz izkrivljenih mnogokotnikov (razen trikotniška teselacija, pri njej moramo vsako oglišče kopirati ter le enega premakniti – tako se trikotniki spremenijo v izkrivljene heksagrame).
| Trikoten “blended“
s segmentom apeiroeder |
Kvadraten “blended“
s segmentom apeiroeder |
Šestkoten “blended“
s segmentom apeiroeder |
Petrialni trikoten “blended“
s segmentom apeiroeder |
Petrialni kvadraten “blended“
s segmentom apeiroeder |
Petrialni šestkoten “blended“
s segmentom apeiroeder | |
|---|---|---|---|---|---|---|
| Schläflijev simbol | {3, 6} # {} | {4, 4} # {} | {6, 3} # {} | {∞, 6}3 # {} | {∞, 4}4 # {} | {∞, 3}6 # {} |
| osnovna ploskev | izkrivljen trikotnik | izkrivljen kvadrat | izkrivljen šestkotnik | nesklenjeni cikcaki | ||
| simetrija | šestkratna rotacijska | štirikratna rotacijska | trikratna rotacijska | šestkratna rotacijska | štirikratna rotacijska | trikratna rotacijska |
| dual | šestkotno “blended“
s segmentom tlakovanje |
sam sebi | trikotno “blended“
s segmentom tlakovanje |
/ | ||

Pri “blended” teselacijah z apeiroedrom nadomestimo stranske ploskve planarnih teselacij zamenjamo z linearnim apeiroedrom z enako simetrijo kot mnogokotnik, ki ga nadomešča (notranji kot mnogokotnika mora biti enak kotu, ki je vzporeden z ravnino nekdanjega planarnega poliedra v vijačnici). Tako nastane osnovna ploskev vijačnica in pri petrialih cikcak. Vijačnicam moramo periodično izmenjevati orientacijo, da imajo lahko skupna oglišča. Vijačnici se lahko določi kot, ki je vzporeden na ravnino (60°, 90° in 120°, saj morajo imeti enako simetrijo kot mnogokotniki, katere nadomeščajo).
| Trikoten “blended“
z apeiroedrom apeiroeder |
Kvadraten “blended“
z apeiroedrom apeiroeder |
Šestkoten “blended“
z apeiroedrom apeiroeder |
Petrialni trikoten “blended“ z
apeiroedrom apeiroeder |
Petrialni kvadraten “blended“ z
apeiroedrom apeiroeder |
Petrialni šestkoten “blended“
z apeiroedrom apeiroeder | |
|---|---|---|---|---|---|---|
| Schläflijev simbol | {3, 6} # {∞} | {4, 4} # {∞} | {6, 3} # {∞} | {∞, 6}3 # {∞} | {∞, 4}4 # {∞} | {∞, 3}6 # {∞} |
| osnovna ploskev | nesklenjeni cikcaki | |||||
| simetrija | šestkratna rotacijska | štirikratna rotacijska | trikratna rotacijska | šestkratna rotacijska | štirikratna rotacijska | trikratna rotacijska |
| dual | šestkoten “blended“
z apeiroedrom apeiroeder |
sam sebi | trikoten “blended“
z apeiroedrom apeiroeder |
/ | ||
Nepopolne planarne teselacije[uredi | uredi kodo]
Poznamo tudi dve nepopolni planarni teselaciji, to sta {∞, 2} in njen dual, {2, ∞}. Prvi je apeirogonalni dieder iz dveh apeirogonov, vsak pokriva polovico ravnine. Njegov dual, apeirogonalni hozoeder, izgleda kot neskončno zaporedje paralelnih premic. Oba imata dvakratno rotacijsko simetrijo.
| Apeirogonalni
dieder |
Apeirogonalni
hozoeder | |
|---|---|---|
| slika | 
|

|
| Schläflijev simbol | {∞, 2} | {2, ∞} |
Dokazovanje pravilnih teselacij[uredi | uredi kodo]
Z naslednjim dokazom lahko dokažemo, da obstaja le 18 različnih pravilnih teselacij:[2]
Naj bo planarni apeirogon s simetrijsko grupo . Za začetno oglišče velja ter in sta nekomutativni involuciji v . Tako morata biti in sekajoči se premici. Sedaj moramo ugotoviti kote, ki so lahko med njima.
Naj bo samostojna neskončna grupa izometrij, ki se disperzirajo na ali , . naj bo podgrupa celotne grupe izometrij v , . Tako ne more imeti netrivialnih nespremenljivih podprostorov. Bieberbachov teorem nam pove, da vsebuje polno podgrupo grupe premikov v , in da je končen; se lahko predstavlja kot mrežo -tega ranka v . Če je glavni element , z (ortogonalni grupi) in premični vektor , potem preslikave tvorijo podrugrupo G0 od On, ki se imenuje posebna grupa od . Tako je slika pod homomorfizmom na In, katerega kernel je : . Lahko predvidevamo, da vsebuje centralno inverzijo – če je nima, jo dodamo. Predvidevajmo sedaj, da je in da vsebuje rotacijo s periodo ; potem vsebuje tako rotacijo skozi kot . Začnimo s primerom . Ker je , lahko predvidevamo, da je sod. Med premiki je minimalna razdalja . Če ima , potem je razdalja med in , kar je protislovje. Za navadnega prostora dokažemo podobno, le da upoštevamo najkrajšo razdaljo med paralelnimi osmi k-kratne simetrije. Če upoštevamo samostojne pravilne politope višjega ranka v vidimo, da so tri pravilne teselacije planarne, prav tako kot njihovi petriali. Vidimo lahko tudi 12 različnih trodimenzionalnih pravilnih poliedrov.
Iz nastalih apeiroedrov je razvidno, da so edini možni koti med in 30°, 60° in 45°. je lahko premica ali točka. V prvem primeru mora biti [4, 4] ali [3, 6], ki nam da tri klasične planarne teselacije. V drugem primeru je komutativna z , torej mora ležati v ter tako dobimo še tri petriale.
Na enak način se lahko tudi dokaže, da obstaja 12 “blended” apeiroedrov.
Pravilni poševni apeiroedri (Petrie-Coxeterjevi apeiroedri in čisti poševni apeiroedri)[uredi | uredi kodo]

Harold Scott MacDonald Coxeter je trdil, da definicija, ki jo je podal John Flinders Petrie (sedaj znana kot Petrie-Coxeterjeva definicija) dovoljuje tudi končne pravilne poševne poliedre v štirih dimenzijah ter pravilne poševne apeiroedre v treh dimenzijah (opisani tukaj). Coxeterju je uspelo najti tri izmed šestih apeiroedrov, ki jih sedaj imenujemo Petrie-Coxeterjevi apeiroedri. Iz njih se lahko dobi tudi šest drugačnih apeiroedrov, katere imenujemo čisti poševni apeiroedri.
Coxeter je ponudil Schläflijeve simbole v obliki {p, q|n}, kjer n označuje n-kotne luknje, ki se pojavljajo med stranskimi ploskvami.
| Mukocka | Muoktaeder | Mutetraeder | Petrialna
mukocka |
Petrialni
muoktaeder |
Petrialni
mutetraeder | |
|---|---|---|---|---|---|---|
| slika (narisan le
en del apeiroedra) |

|

|

|
|||
| animacija (le en
del apeiroedra) |

|

|

|
|||
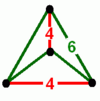
| slika oglišč | 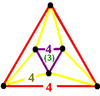
|
|
|
|||
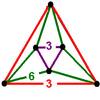
| Schläflijev simbol | {4, 6|4} | {6, 4|4} | {6, 6|3} | {∞, 6}4,4 | {∞, 4}6,4 | {∞,6}6,3 |
| osnovna ploskev | kvadrat | šestkotnik | šestkotnik | nesklenjeni cikcaki | ||
| oblika lukenj | kvadrat | kvadrat | trikotnik | / | ||
| simetrija | razširjena kiralna | |||||
| dual | muoktaeder | mukocka | mutetraeder | / | ||
Branko Grünbaum in Andreas Dress sta nato še iz preoblikovanja Petrie-Coxeterjevih apeiroedrov dobila 6 novih apeiroedrov, ki jih sedaj imenujemo čisti poševni apeiroedri.
| Razpolovljena
mukocka |
Petrialna
rapolovljena mukocka |
Izkrivljen
petrialni mutetraeder |
Izkrivljen
muoktaeder |
Facetirana
razpolovljena mukocka |
Petrialna
facetirana razpolovljena mukocka | |
|---|---|---|---|---|---|---|
| Schläflijev simbol | {6, 6}4 | {4, 6}6 | {6, 4}6 | {∞, 4}·,∗3 | {∞, 3}(a) | {∞, 3}(b) |
| osnovna ploskev | izkrivljen šestkotnik | izkrivljen kvadrat | izkrivljen šestkotnik | cikcaki | ||
| simetrija | razširjena kiralna | |||||
| dual | / | izkrivljen
petrialni mutetraeder |
petrialna
rapolovljena mukocka |
/ | ||
Razmerja med pravilnimi poševnimi ploiedri so naslednja[2]:
| Razpolovljena
mukocka |
Petrialna
rapolovljena mukocka |
Dual petrialne
razpolovljene mukocke |
Izkrivljen
muoktaeder |
Facetirana
razpolovljena mukocka |
Petrialna
facetirana razpolovljena mukocka | |
|---|---|---|---|---|---|---|
| z mukocko |
|
| ||||
| z muoktaedrom |
|
| ||||
| z mutetraedrom |
|
|
Pri razmerjih v zgornji tabeli −1 pomeni, da je obratno razmerje (le pri tistih, kjer je obratno razmerje drugačno):
Dokazovanje pravilnih poševnih apeiroedrov[uredi | uredi kodo]
Z naslednjim dokazom lahko dokažemo, da obstaja le 12 pravilnih poševnih apeiroedrov[2]:
Naj bo čisti tridimenzionalni apeiroeder v (teoretično so tudi Petrie-Coxeterjevi apeiroedri čisti, saj ni nobene razlike, ki bi jih naredila manj “čiste”), s simetrijsko grupo . Tako so , in involucijske izometrije tako, da sta in komutativni, pa ni komutativna z niti z niti z .
Najprej moramo dokazati, da mora biti vsaka izmed , in premica ali ravnina, z drugimi besedami, izključimo lahko zrcaljenje čez točko. Naj bo izhodiščno oglišče -ja . Potem dobimo , torej ne sme biti presek prazen ter mora biti znotraj in , zato je dimenzija za . Za te vrednosti zapišemo ali , saj je ortogonalni komplement in za ravnino skozi , ki je pravokotna na in . Tako . Če bi bila , bi bil reducibilen, saj bi vsaka permutirala ravnine, pravokotne na , kar je v protislovju s predvidevanjem, da je čisti. Dobili bi , saj sta simetriji komutativni. Tako je tudi dimenzija .
Sedaj moramo izključiti možnost, da je dimenzija za . V takem primeru bi obe ravnini šli skozi ter se sekali pod nekim ostrim kotom. je tako premica ali ravnina, katere zrcaljenje je komutativno z , vendar ne z . Če je ravnina bi zaradi ireducibilnosti sledilo, da , torej bi bila samostojna ortogonalna grupa in zato končna. Če je premica imamo dve možnosti. lahko leži v , kar bi spet povzročilo ter bi tako bila končna. Druga možnost je, da je pravokotna na . To naredi grupo reducibilno, kar ni dovoljeno.
Izključiti moramo še možnost, da bi lahko bila dimenzija in . Če bi to bilo možno, bi bila pravokotna na (ker je možnost prepovedana). Kot v prejšnjem primeru bi to naredilo grupo reducibilno, česar ne dovoljujemo.
Tako lahko dimenzijski vektor (dimenzija , dimenzija , dimenzija ) za zrcala lahko le štirih vrednosti: (2, 1, 2), (1, 1, 2), (1, 2, 1) in (1, 1, 1).
Določili smo že planarno zrcaljenje in . Sedaj moramo definirati še tretje zrcaljenje, , katere zrcalo je prav tako ravnina. Naj bo premamknjena , ki vsebuje izhodišče in nato nastavimo ali , saj je premica ali ravnina. Naj bo nato , ki je posebna grupa od in . Potem je končna ireducibilna zrcalna grupa, poimensko, ena izmed [3, 3], [3, 4] ali [3, 5] in je ali ena izmed naštetih zrcalnih grup ali njihova rotacijska podgrupa (to se lahko zgodi le, ko je dimenzija za vsak . Ker mora biti samostojen, ne more biti [3, 5] ali njegova rotacijska subgrupa, saj smo že pri pravilnih teselacijah izključili petkratne rotacije. mora tako biti [3, 3] ali [3, 4]. S štirimi možnostimi za vektor in tremi za gupo (lahko je tudi [4, 3]) lahko vidimo, da imamo 12 možnosti. Vseh 12 obstaja.
Tako dobimo naslednjo tabelo:
| {3, 3} | {3, 4} | {4, 3} | |
|---|---|---|---|
| (2, 1, 2) | {6, 6|3} | {6, 4|4} | {6, 4|4} |
| (1, 1, 2) | {∞, 6}4, 4 | {∞, 4}6, 4 | {∞,6}6,3 |
| (1, 2, 1) | {6, 6}4 | {6, 4}6 | {4, 6}6 |
| (1, 1, 1) | {∞, 3}(a) | {∞, 4}·,∗3 | {∞, 3}(b) |
Pravilne teselacije izven evklidskega prostora[uredi | uredi kodo]
Že prej so bile omenjene pravilne teselacije evklidskega prostora, obstajajo pa tudi pravilne teselacije sferičnega prostora (povšine krogle) in hiperboličnega prostora. Obstaja neskončno različnih teselacij zunaj evklidskega prostora, saj je možna katerakoli kombinacija {p, q} za p, q >1. Poznamo še dve izjemi, to sta enostrani hozoeder {2, 1} in enostrani dieder {1, 2}. Poliedri s Schläflijevim simbolom {2, n} (hozoedri) in {n, 2} (diedri) se imenujejo nepopolni poliedri, saj obstajajo v Evklidskem prostoru šele, ko je n = ∞. Poleg nepopolnih poznamo še platonske teselacije, ki so sferične različice platonskih teles. Tako, kot platonskih teles, je tudi teh 5. Za vse sferične teselacije je značilno:
Iz enačbe lahko tudi razberemo, zakaj nepopolni poliedri obstajajo v Evklidskem prostoru šele v neskončnosti. Za hiperbolične teselacije velja naslednja enačba:
Vrednosti p in q so lahko tako neskončne za p in q. Hiperbolične teselacije, ki imajo končen p in q se imenujejo kompaktne, saj jih lahko nekje zaključimo, čeprav ne bi pokrivale celotne (hiperbolične) ravnine. Teselacije z neskončnim število p ali q se imenujejo parakompaktne, saj bi jih lahko nekje zaključili, vendar šele v neskončnosti. Obstaja pa še tretja možnost, ko sta p ali q enaka iπ/λ, kar je le oznaka za drugo vrsto neskončnosti, vendar se takrat stranice nikoli, niti v neskončnosti ne staknejo. Take teselacije imenujemo nekompaktne, saj jih ne moremo zaključiti.
| Sferni (nepopolni, platonski), Evklidski, hiperbolični (Poincaréjev disk projekcija: kompaktni, parakompaktni, nekompaktni) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p \ q | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... | ∞ | ... | iπ/λ |
| 0 |
{0, 0} ravnina brez robov[5] |
||||||||||||
| 1 | {1, 2} enostrani dieder |
||||||||||||
| 2 |  {2, 1} enostrani hozoeder |
 {2, 2} dvostrani hozoeder |
 {2, 3} trostrani hozoeder |
 {2, 4} štiristrani hozoeder |
 {2, 5} petstrani hozoeder |
 {2, 6} šeststrani hozoeder |
 {2, 7} sedemstrani hozoeder |
 {2, 8} osemstrani hozoeder |
 {2, ∞} apeirogonalni hozoeder |
 {2, iπ/λ}
| |||
| 3 |  {3, 2} tristrani dieder |
 {3, 3} tetraeder |
 {3, 4} oktaeder |
 {3, 5} ikozaeder |
 {3, 6} trikotno tlakovanje |
 {3, 7}
|
 {3, 8}
|
 {3, ∞}
|
 {3, iπ/λ}
| ||||
| 4 |  {4, 2} štiristani dieder |
 {4, 3} kocka |
 {4, 4} kvadratno tlakovanje |
 {4, 5}
|
 {4, 6}
|
 {4, 7}
|
 {4, 8}
|
 {4, ∞}
|
 {4, iπ/λ}
| ||||
| 5 |  {5, 2} petstrani dieder |
 {5, 3} |
 {5, 4} |
 {5, 5} |
 {5, 6}
|
 {5, 7}
|
 {5, 8}
|
 {5, ∞}
|
 {5, iπ/λ}
| ||||
| 6 |  {6, 2} šeststrani |
 {6, 3} šestkotno |
 {6, 4}
|
 {6, 5}
|
 {6, 6}
|
 {6, 7}
|
 {6, 8}
|
 {6, ∞}
|
 {6, iπ/λ}
| ||||
| 7 | {7, 2} sedemstrani dieder |
 {7, 3}
|
 {7, 4}
|
 {7, 5}
|
 {7, 6}
|
 {7, 7}
|
{7, 8}
|
 {7, ∞}
|
{7, iπ/λ}
| ||||
| 8 | {8, 2} osemstrani dieder |
 {8, 3}
|
 {8, 4}
|
 {8, 5}
|
 {8, 6}
|
 {8, 7}
|
 {8, 8}
|
 {8, ∞}
|
{8, iπ/λ}
| ||||
| ... | |||||||||||||
| ∞ |  {∞,2} apeirogonalni dieder |
 {∞,3}
|
 {∞,4}
|
 {∞,5}
|
 {∞, 6}
|
 {∞,7}
|
 {∞,8}
|
 {∞,∞}
|
 {∞,iπ/λ}
| ||||
| ... | |||||||||||||
| iπ/λ |  {iπ/λ,2} |
 {iπ/λ,3} |
 {iπ/λ,4} |
 {iπ/λ,5} |
 {iπ/λ,6} |
{iπ/λ,7} |
{iπ/λ,8} |
 {iπ/λ,∞} |
{iπ/λ,iπ/λ} | ||||
Pravilne teselacije s steliranimi mnogokotniki[uredi | uredi kodo]
Poznamo dve sferni teselaciji (mali stelirani dodekaeder in veliki dodekaeder, ostali Kepler-Poinsotovi telesi nimata ene izmed kombinacij, predstavljenih v nadaljevanju) ter nobene v Evklidskem. Čeprav je veliko kombinacij, ki ustrezajo enačbi 1p + 1q = 12, npr. {83, 8}, {103, 5} {52, 10}, {125, 12} … se nobena izmed kombinacij ne ponavlja periodično. Edini dve možnosti za pravilne teselacije so {p2, p} in njegov dual, {p, p2} za vsak oz. če je p liho število, večje od 5. Če je število sodo dobimo ali degenerirane dvojne ovoje ali teselacijske sestave. Možnih pravilnih teselacij je tako neskončno, vendar števila p ne smemo nadomestiti z neskončno, saj neskončnosti se ne da določiti ali je liha ali ne. Vse teselacije imajo gostoto 3.
| Sferični, hiperbolični (Poincaréjev disk projekcija) | |||||
|---|---|---|---|---|---|
| 5 | 7 | 9 | 11 | ... | |
| {p2, p} | 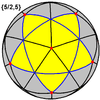
{52, 5} |

{72, 7} |
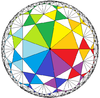
{92, 9} |

{112, 11} | |
| {p, p2} | 
{5, 52} |

{7, 72} |

{9, 92} |

{11, 112} | |
Teselacije realne projektivne ravnine[uredi | uredi kodo]
Realna projektivna ravnina () je neorientabilna ravnina, katero lahko pokrivamo s pravilnimi abstraktnimi poliedri. To lahko naredimo s projektivnimi dvojniki platonskih teles, to so polkocka, poloktaeder, poldodekaeder in polikozaeder. Tetraeder nima svojega projektivnega dvojnika, saj nima vzporednih stranskih ploskev, ki bi jih lahko združili v eno. Tako kot pri sfernem tlakovanju, lahko tudi tukaj tlakujemo celotno ravnino s končnim številom stranskih ploskev. Druga možnost je z poldiedri in polhozoedri, katerih je neskončno, saj lahko vsakemu s sodim Schläflijevim simbolom določimo projektivnega dvojnika[6]. Od sfernega tlakovanja se te teselacije razlikujejo v Eulerjevi karakteristiki, saj je tu 1 in je neorientabilna.
| Polkocka | Poloktaeder | Poldodekaeder | Polikozaeder | Polhozoeder | Poldieder | |
|---|---|---|---|---|---|---|
| slika (narisana v evklidskem
prostoru, zato se nekatera oglišča pojavljajo večkrat) |

|

|

|

|
||
| Schläflijev simbol | {4, 3} | {3, 4} | {3, 5} | {5, 3} | {2, 2n} | {2n, 2} |
| št. stranskih ploskev | 3 | 4 | 6 | 10 | 2n | 2 |
| št. oglišč | 4 | 3 | 10 | 6 | 2 | 2n |
| št. robov | 6 | 6 | 15 | 15 | 2n + 1 | 2n + 1 |
| Eulerjeva karakteristika | 1 | 1 | 1 | 1 | 1 | 1 |
| dual | poloktaeder | polkocka | polikozaeder | poldodekaeder | poldieder | polhozoeder |
Teselacije torusa[uredi | uredi kodo]
Teselacije torusa izhajajo iz evklidskih teselacij – trikotne, kvadratne in šestkotne, le da so na torusu končne. Tako obstaja več možnosti za število stranskih ploskev in samo orientacijo stranskih ploskev. Ker imajo vse enak Schläflijev simbol, moramo na koncu navesti še dve števili (m, n), ki označujeta število stranskih ploskev in kot.
Kvadratne teselacije so možne za m > 0. Za vsak m je možnih m + 1 različnih teselacij. Dual teselacije je teselacija sama.[7]
| m = 1 | m = 2 | m = 3 | … | |
|---|---|---|---|---|
| n = 0 | {4, 4}(1, 0) |

{4, 4}(2, 0) |

{4, 4}(3,0) | |
| n = 1 | 
{4, 4}(1, 1) |

{4, 4}(2, 1) |

{4, 4}(3, 1) | |
| n = 2 | 
{4, 4}(2, 2) |

{4, 4}(3, 2) | ||
| n = 3 | 
{4, 4}(3, 3) |
Šestkotne in trikotne teselacije so druga drugi dual. Možne so za vsak m ≥ 0, vendar za sod m je lahko n le sod in za lih m je lahko n le lih, prav tako n ne more biti manjši od m.
| n \ m | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 
{6, 3}(1, 1) {3, 6}(1, 1) |
||||||||
| 2 | 
{6, 3}(0, 2) {3, 6}(0, 2) |

{6, 3}(2, 2) {3, 6}(2, 2) |
|||||||
| 3 | 
{6, 3}(1, 3) {3, 6}(1, 3) |

{6, 3}(3, 3) {3, 6}(3, 3) |
|||||||
| 4 | 
{6, 3}(0, 4) {3, 6}(0, 4) |
{6, 3}(2, 4)
{3, 6}(2, 4) |

{6, 3}(4, 4) {3, 6}(4, 4) |
||||||
| 5 | 
{6, 3}(1, 5) {3, 6}(1, 5) |

{6, 3}(3, 5) {3, 6}(3, 5) |

{6, 3}(5, 5) {6, 3}(5, 5) |
||||||
| 6 | 
{6, 3}(0, 6) {3, 6}(0, 6) |

{6, 3}(2, 6) {6, 3}(2, 6) |

{6, 3}(4, 6) {3, 6}(4, 6) |

{6, 3}(6, 6) {3, 6}(6, 6) |
|||||
| 7 | 
{6, 3}(1, 7) {3, 6}(1, 7) |

{6, 3}(3, 7) {3, 6}(3, 7) |

{6, 3}(5, 7) {3, 6}(5, 7) |

{6, 3}(7, 7) {3, 6}(7, 7) | |||||
| … | |||||||||
Število oglišč, stranskih ploskev in robov so naslednje:[7]
| (m, n) | kvadratne teselacije | (m, n) | trikotne teselacije | šestkotne teselacije |
|---|---|---|---|---|
| (1, 0) | V = 1
F = 1 E = 2 |
(0, 2) | V = 3
F = 6 E = 9 |
V = 6
F = 3 E = 9 |
| (1, 1) | V = 2
F = 2 E = 4 |
(0, 4) | V = 12
F = 24 E = 36 |
V = 24
F = 12 E = 36 |
| (2, 0) | V = 4
F = 4 E = 8 |
(0, 6) | V = 27
F = 54 E = 81 |
V = 54
F = 27 E = 81 |
| (2, 1) | V = 5
F = 5 E = 10 |
(0, 8) | V = 48
F = 96 E = 144 |
V = 96
F = 48 E = 144 |
| (2, 2) | V = 8
F = 8 E = 16 |
(0, 10) | V = 75
F = 150 E = 225 |
V = 150
F = 75 E = 225 |
| (3, 0) | V = 9
F = 9 E = 18 |
(0, 12) | V = 108
F = 216 E = 324 |
V = 216
F = 108 E = 324 |
| (3, 1) | V = 10
F = 10 E = 20 |
(0, 14) | V = 147
F = 294 E = 441 |
V = 294
F = 147 E = 441 |
| (3, 2) | V = 13
F = 13 E = 26 |
(0, 16) | V = 192
F = 384 E = 576 |
V = 384
F = 192 E = 576 |
| (3, 3) | V = 18
F = 18 E = 36 |
(1, 1) | V = 1
F = 2 E = 3 |
V = 2
F = 1 E = 3 |
| (4, 0) | V = 16
F = 16 E = 32 |
(1, 3) | V = 7
F = 14 E = 21 |
V = 14
F = 7 E = 21 |
| (4, 1) | V = 17
F = 17 E = 34 |
(1, 5) | V = 19
F = 38 E = 57 |
V = 38
F = 19 E = 57 |
| (4, 2) | V = 20
F = 20 E = 40 |
(1, 7) | V = 37
F = 74 E = 111 |
V = 74
F = 37 E = 111 |
| (4, 3) | V = 25
F = 25 E = 50 |
(2, 2) | V = 4
F = 8 E = 12 |
V = 8
F = 4 E = 12 |
| (4, 4) | V = 32
F = 32 E = 64 |
(2, 4) | V = 13
F = 26 E = 39 |
V = 26
F = 13 E =39 |
| (5, 0) | V = 25
F = 25 E = 50 |
(2, 6) | V = 28
F = 56 E = 84 |
V = 56
F = 28 E = 84 |
| (5, 1) | V = 26
F = 26 E = 52 |
(2, 8) | V = 49
F = 98 E = 147 |
V = 98
F = 49 E = 147 |
| (5, 2) | V = 29
F = 29 E = 58 |
(3, 3) | V = 9
F = 18 E = 27 |
V = 18
F = 9 E = 27 |
| (5, 3) | V = 34
F = 34 E = 68 |
(3, 5) | V = 21
F = 42 E = 63 |
V = 42
F = 21 E = 63 |
| (5, 4) | V = 41
F = 41 E = 81 |
(3, 7) | V = 39
F = 78 E = 117 |
V = 78
F = 39 E = 117 |
| (5, 5) | V = 50
F = 50 E = 100 |
(4, 4) | V = 16
F = 32 E = 48 |
V = 32
F = 16 E = 48 |
| (6, 0) | V = 36
F = 36 E = 72 |
(4, 6) | V = 31
F = 62 E = 93 |
V = 62
F = 31 E = 93 |
| (6, 1) | V = 37
F = 37 E = 74 |
(5, 5) | V = 25
F = 50 E = 75 |
V = 50
F = 25 E = 75 |
| (6, 2) | V = 40
F = 40 E = 80 |
(5, 7) | V = 43
F = 86 E = 129 |
V = 86
F = 43 E = 129 |
| (6, 3) | V = 45
F = 45 E = 90 |
(6, 6) | V = 72
F = 36 E = 108 |
V = 36
F = 72 E = 108 |
| (6, 6) | V = 36
F = 36 E = 144 |
(7, 7) | V = 49
F = 98 E = 147 |
V = 98
F = 49 E = 147 |
| (7, 0) | V = 49
F = 49 E = 98 |
(8, 8) | V = 48
F = 96 E = 144 |
V = 96
F = 48 E = 144 |
| (7, 1) | V = 50
F = 50 E = 100 |
(10, 10) | V = 75
F = 150 E = 225 |
V = 150
F = 75 E = 225 |
| (7, 7) | V = 49
F = 49 E = 196 |
(12, 12) | V = 108
F = 216 E = 324 |
V = 216
F = 108 E = 324 |
| (8, 0) | V = 64
F = 64 E = 128 |
(14, 14) | V = 147
F = 294 E = 441 |
V = 294
F = 147 E = 441 |
| (8, 1) | V = 64
F = 64 E = 256 |
(16, 16) | V = 192
F = 384 E = 576 |
V = 384
F = 192 E = 576 |
| … | ||||
“Blended” teselacije izven evklidskega prostora[uredi | uredi kodo]
Tako, kot v evkliskem prostoru, lahko tudi v drugih prostorih naredimo “blended” teselacije, to velja tudi za teselacije s steliranimi mnogokotniki, teselacije realne projektivne ravnine in teselacije torusa.
Pravilni poliedrski sestavi[uredi | uredi kodo]
Pravilni sestavi so poliedri, ki so sestavljeni iz več enakih platonskih teles. Telo dobimo ali z združevanjem teles ali s facetiranjem platonskih teles. Tako poznamo 5 različnih pravilnih sestavov. Vsi imajo neko vrsto ikozaederske simetrije razen zvednega oktaedra, saj nastane s facetiranjem kocke. Poznamo tudi dualno pravilne sestave, vendar tukaj niso navedeni, saj niso niti ogliščno prehodni, zato jih le redkokdo uvršča med pravilne poliedre. Pravilnim sestavom se da določiti Schläflijev simbol, vendar se pri njih raje uporablja Coxeterjeve simbole.
| Zvezdni oktaeder | Kiro-ikozaeder | Sestav dveh | Rombieder | Mali
ikoziikozaeder | |
|---|---|---|---|---|---|
| slika | 
|

|

|

|

|
| 3D model | 
|

|

|

| |
| Coxeterjev simbol | {4, 3} [2{3, 3}] {3, 4} | {5, 3} [5{3, 3}] {3, 5} | 2{5, 3} [10{3, 3}] 2{3, 5} | 2{5, 3} [5{4, 3}] | [5{3, 4}] 2{3, 5} |
| nastal z združevanjem | 2 tetraedrov | 5 tetraedrov | 10 tetraedrov | 5 kock | 5 oktaedrov |
| nastal s facetiranjem | kocke | dodekaedra | dodekaedra | dodekaedra | ikozidodekaedra |
| št. stranskih ploskev | 8 | 20 | 40 | 30 | 40 |
| št. oglišč | 8 | 20 | 20 | 20 | 30 |
| št. robov | 12 | 30 | 60 | 60 | 60 |
| Eulerjeva karakteristika | 4 | 10 | 0 | −10 | 10 |
| simetrija | Oh | I | Ih | Ih | Ih |
| dual | sam sebi | kiralni kiro-ikozaeder | sam sebi | mali ikoziikozaeder | rombieder |
Pravilni teselacijski sestavi[uredi | uredi kodo]
Poznamo neskončno pravilnih teselacijskih sestavov, od tega jih je 7 v sferičnem prostoru in 18 oz. 20 (odvisno od vira) v evklidskem. Hiperbolični prostor dopušča neskončno različnih pravilnih teselacijskih sestavov. Sferični teselacijski sestavi so isti kot pravilni poliederski sestavi, dodati moramo le še pravilna sestava hozoedra in diedra. Pri teselacijskih sestavih se pri Coxeterjevem simbolu lahko pojavijo enake številke za različne sestave, zato moramo v simbol vključiti še oz. . Pri hiperboličnih je pri nekaterih primerih q lahko poljubno velik (kar nam da neskončno teselacijskih sestavov), edina omejitev je:
,
saj če bi bil enak 12 bi bil pravilen v evklidkem prostoru, če bi bil večji od tega pa bi bil pravilen v sferičnem prostoru. Za seznam se domneva, da je zaključen, saj že dolgo ni bilo odkritega novega sestava, vendar tega še niso dokazali.[8]
| Coxeterjev simbol | slika | nastal z združevanjem | dual |
|---|---|---|---|
| {4, 3} [2{3, 3}] {3, 4} | 
|
2 tetraedrov | sam sebi |
| {5, 3} [5{3, 3}] {3, 5} | 
|
5 tetraedrov | sam sebi |
| 2{5, 3} [10{3, 3}] 2{3, 5} | 
|
10 tetraedrov | sam sebi |
| 2{3, 4} [3{4, 2}] {4, 3} | 
|
3 štiristranih diedrov | {3, 4} [3{2, 4}] 2{4, 3} |
| {3, 4} [3{2, 4}] 2{4, 3} | 
|
3 štiristranih hozoedrov | 2{3, 4} [3{4, 2}] {4, 3} |
| 2{5, 3} [5{4, 3}] | 
|
5 kock | [5{3, 4}] 2{3, 5} |
| [5{3, 4}] 2{3, 5} | 
|
5 oktaedrov | 2{5, 3} [5{4, 3}] |
| Coxeterjev simbol | slika | nastal z združevanjem | dual |
|---|---|---|---|
| {4, 4} [(b2 + c2) {4, 4}] {4, 4} | kvadratnega tlakovanja | sam sebi | |
| 2{4, 4} [2(b2 + c2) {4, 4}] 2{4, 4} | 
|
2 kvadratnih tlakovanj | sam sebi |
| {3, 6} [(b2 + bc + c2) {3, 6}] 2{6, 3} | trikotnega tlakovanja | 2{3, 6} [(b2 + bc + c2) {6, 3}] {6, 3} | |
| 2{3, 6} [(b2 + bc + c2) {6, 3}] {6, 3} | šestkotnega tlakovanja | {3, 6} [(b2 + bc + c2) {3, 6}] 2{6, 3} | |
| 2{3, 6} [2(b2 + bc + c2) {3, 6}] 4{6, 3} | 2 trikotnih tlakovanj | 4{3, 6} [2(b2 + bc + c2) {6, 3}] 2{6, 3} | |
| 4{3, 6} [2(b2 + bc + c2) {6, 3}] 2{6, 3} | 2 šestkotnih tlakovanj | 2{3, 6} [2(b2 + bc + c2) {3, 6}] 4{6, 3} | |
| {6, 3} [2(b2 + bc + c2) {3, 6}] 2{3, 6} | 2 trikotnih tlakovanj | 2{6, 3} [2(b2 + bc + c2) {6, 3}] {3, 6} | |
| 2{6, 3} [2(b2 + bc + c2) {6, 3}] {3, 6} | 2 šestkotnih tlakovanj | {6, 3} [2(b2 + bc + c2) {3, 6}] 2{3, 6} | |
| 2{6, 3} [4(b2 + bc + c2) {3, 6}] 4{3, 6} | 4 trikotnih tlakovanj | 4{6, 3} [4(b2 + bc + c2) {6, 3}] 2{3, 6} | |
| 4{6, 3} [4(b2 + bc + c2) {6, 3}] 2{3, 6} | 4 šestkotnih tlakovanj | 2{6, 3} [4(b2 + bc + c2) {3, 6}] 4{3, 6} | |
| {3, 6} [(b2 + bc + c2) {3, 6}] {3, 6} | trikotnega tlakovanja | {6, 3} [(b2 + bc + c2) {6, 3}] {6, 3} | |
| {6, 3} [(b2 + bc + c2) {6, 3}] {6, 3} | šestkotnega tlakovanja | {3, 6} [(b2 + bc + c2) {3, 6}] {3, 6} | |
| 2{3, 6} [2(b2 + bc + c2) {3, 6}] 2{3, 6} | 2 trikotnih tlakovanj | 2{6, 3} [2(b2 + bc + c2) {6, 3}] 2{6, 3} | |
| 2{6, 3} [2(b2 + bc + c2) {6, 3}] 2{6, 3} | 2 šestkotnih tlakovanj | 2{3, 6} [2(b2 + bc + c2) {3, 6}] 2{3, 6} | |
| {6, 3} [2(b2 + bc + c2) {3, 6}] | 
|
2 trikotnih tlakovanj | [2(b2 + bc + c2) {6, 3}] {3, 6} |
| [2(b2 + bc + c2) {6, 3}] {3, 6} | 
|
2 šestkotnih tlakovanj | {6, 3} [2(b2 + bc + c2) {3, 6}] |
| 2{6, 3} [4(b2 + bc + c2) {3, 6}] | 4 trikotnih tlakovanj | [4(b2 + bc + c2) {6, 3}] 2{3, 6} | |
| [4(b2 + bc + c2) {6, 3}] 2{3, 6} | 4 šestkotnih tlakovanj | 2{6, 3} [4(b2 + bc + c2) {3, 6}] |
Nekateri izmed virov prištevajo tudi naslednja dva sestava:
| Coxeterjev simbol | slika | nastal z združevanjem | dual |
|---|---|---|---|
| {3, 6} [3{3, 6}] 2{6, 3} | 
|
3 trikotnih tlakovanj | 2{3, 6} [3{6, 3}] {6, 3} |
| 2{3, 6} [3{6, 3}] {6, 3} | 
|
3 šestkotnih tlakovanj | {3, 6} [3{3, 6}] 2{6, 3} |

| Coxeterjev simbol | nastal z združevanjem | dual |
|---|---|---|
| {4, q} [2{q, q}] {q, 4} | 2 {q, q} | sam sebi |
| {3, 8} [6{8, 8}] {8, 3} | 6 {8, 8} | sam sebi |
| {5, 5} [6{10, 10}] {5, 5} | 6 {10, 10} | sam sebi |
| {4, 5} [12{10, 10}] {5, 4} | 12 {10, 10} | sam sebi |
| {3, 7} [9{7, 7}] {7, 3} | 9 {7, 7} | sam sebi |
| 2{3, 7} [18{7, 7}] 2{7, 3} | 18 {7, 7} | sam sebi |
| {3, 2q} [3{q, 2q}] 2{2q, 3} | 3 {q, 2q} | 2{3, 2q} [3{2q, q}] {2q, 3} |
| 2{3, 2q} [3{2q, q}] {2q, 3} | 3 {2q, q} | {3, 2q} [3{q, 2q}] 2{2q, 3} |
| {4, 5} [6{4, 10}] 2{4, 5} | 6 {4, 10} | 2{5, 4} [6{10, 4}] {5, 4} |
| 2{5, 4} [6{10, 4}] {5, 4} | 6 {10, 4} | {4, 5} [6{4, 10}] 2{4, 5} |
| {3, 7} [8{3, 14}] 2{3, 7} | 8 {3, 14} | 2{7, 3} [8{14, 3}] {7, 3} |
| 2{7, 3} [8{14, 3}] {7, 3} | 8 {14, 3} | {3, 7} [8{3, 14}] 2{3, 7} |
| {3, 7} [24{7, 14}] 2{7, 3} | 24 {7, 14} | 2{3, 7} [24{14, 7}] {7, 3} |
| 2{3, 7} [24{14, 7}] {7, 3} | 24 {14, 7} | {3, 7} [24{7, 14}] 2{7, 3} |
| {3, 9} [12{9, 18}] 2{9, 3} | 12 {9, 18} | 2{3, 9} [12{18, 9}] {9, 3} |
| 2{3, 9} [12{18, 9}] {9, 3} | 12 {18, 9} | {3, 9} [12{9, 18}] 2{9, 3} |
| {2q, q} [2{q, 2q}] | 2 {q, 2q} | [2{2q, q}] {q, 2q} |
| [2{2q, q}] {q, 2q} | 2 {2q, q} | {2q, q} [2{q, 2q}] |
| 2{3, 7} [9{4, 7}] | 9 {4, 7} | [9{7, 4}] 2{7, 3} |
| [9{7, 4}] 2{7, 3} | 9 {7, 4} | 2{3, 7} [9{4, 7}] |
| {3, 9} [4{3, 18}] | 4 {3, 18} | [4{18, 3}] {9, 3} |
| [4{18, 3}] {9, 3} | 4 {18, 3} | {3, 9} [4{3, 18}] |
“Blended” teselacijski sestavi[uredi | uredi kodo]
Načeloma lahko imajo vsi teselacijski sestavi tudi svoji “blended” različici, vendar ni preverjeno, ali so potem še vedno pravilni sestavi. To področje je še zelo neraziskano.
Kompleksni poliedri[uredi | uredi kodo]
Poznamo 3 kompleksne poliedre in dve neskončni družini, ki jih je opisal Coxeter. Coxeter je v svoj seznam vključeval tudi Platonska telesa, vendar ker smo te že predstvaili, jih na tem seznamu ni.
| 3{3}3{3}3 | 2{4}3{3}3 | 3{3}3{4}2 | 2{3}2{4}p | p{4}2{3}2 | |
|---|---|---|---|---|---|
| p > 1 | |||||
| slika | 
|

|

|
glej spodnjo
preglednico | |
| stranska ploskev | 3{3}3 |

2{4}3 |
3{3}3 |
trikotnik
{3} |
p{4}2 |
| rob | 3{} | {} | 3{} | {} | p{} |
| Coxeterjevo število | 9 | 18 | 3p | ||
| št. oglišč | 27 | 54 | 72 | 3p | p3 |
| št. stranskih ploskev | 27 | 72 | 54 | p3 | 3p |
| št. robov | 72 | 216 | 216 | 3p2 | 3p2 |
| Eulerjeva karakteristika | −18 | −90 | −90 | ||
| slika oglišča | 3{3}3 | 3{3}3 | 3{4}2 | 2{4}p | trikotnik
{3} |
Neskončni družini se v bistvu začneta že z evklidskimi poliedri. Kocka in oktaeder nastaneta, ko je p = 2. Tako pogosto imenujemo družini kot družina kompleksnih kock in družina kompleksnih oktaedrov. Naslednji seznam prikazuje prvih deset teles iz vsake družine, vključno z oktaedrom in heksaedrom (kocko). Kocka in oktaeder sta iz svoje slike neprepoznavna, saj smo ju projecirali na enak način, kot ostale, katerih ne moremo projecirati na ravnino na nam bolj intuitiven način.
| p | 2 (platonski telesi) | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 2{3}2{4}p
oktaederska skupina |

|

|

|

|

|

|

|

|

|
… |
| p{4}2{3}2
heksaederska skupina |

|

|

|

|

|

|

|

|

|
Poliedri v višjih dimenzijah[uredi | uredi kodo]
Končni pravilni poševni poliedri obstojajo v štirirazsežnem prostoru. Ti končni poševni poliedri v štiri razsežnem prostoru se lahko obravnavajo kot podmnožica stranskih ploskev uniformnega polihorona. Dve dualni rašitvi sta povezani s 5-celico, dve dualni rešitvi sta povezani s 24-celico. Neskončna množica sebi dualnih duoprizem generira pravilne poševne poliedre z {4,4|n}. V neskončnosti limiti se približujejo duocilindru in izgleda kot torus v stereografski projekciji v trirazsežni prostor.
| Ortogonalne projekcije na Coxeterjevo ravnino | Stereografska projekcija | |||
|---|---|---|---|---|
| A4 | F4 | |||

|

|

|

|

|
| {4, 6 | 3} | {6, 4 | 3} | {4, 8 | 3} | {8, 4 | 3} | {4, 4 | n} |
Abstraktni pravilni poliedri[uredi | uredi kodo]
V današnjem času se poliedri se razumejo kot tri razsežne splošne oblike politopov v poljubnem številu razsežnosti.
Polieder 
srednji rombski triakontaeder
dodekadodekaeder
srednji triambskiikozaeder
ditrigonalni dodekadodekaeder
izkopan dodekaederSlika oglišč {5}, {5/2} 

(5.5/2)2 
{5}, {5/2} 

(5.5/3)3 

Stranske ploskve 30 rombov 
12 petkotnikov
12 pentagramov

20 šestkotnikov 
12 petkotnikov
12 pentagramov

20 šestkotnikov 
Tlakovanje 
{4, 5}
{5, 4}
{6, 5}
{5, 6}
{6, 6}
Glej tudi[uredi | uredi kodo]
Sklici[uredi | uredi kodo]
- ↑ Hubart, Isabel (5. april 2019). »Petrie-Coxeter Maps Revisited« (PDF). Pridobljeno 7. decembra 2020.
- ↑ 2,00 2,01 2,02 2,03 2,04 2,05 2,06 2,07 2,08 2,09 2,10 McMullen, P.; Schulte, E. (1. junij 1997). »Regular Polytopes in Ordinary Space«. Discrete & Computational Geometry (v angleščini). Zv. 17, št. 4. str. 449–478. doi:10.1007/PL00009304. ISSN 1432-0444.
- ↑ 3,0 3,1 Liu, Allen. »The Stars Above Us: Regular and Uniform Polytopes up to Four Dimensions« (PDF). Univerza Harvard. Pridobljeno 7. decembra 2020.
- ↑ Chen; Liang (2006).
- ↑ »Regular Map database - list for manifold«. www.weddslist.com. Pridobljeno 12. decembra 2020.
- ↑ »Regular maps in the projective plane«. www.weddslist.com. Pridobljeno 12. decembra 2020.
- ↑ 7,0 7,1 7,2 7,3 »Regular Map database - list for manifold«. www.weddslist.com. Pridobljeno 12. decembra 2020.
- ↑ 8,0 8,1 8,2 8,3 Coxeter, H. S. M. (1964). »Regular Compound Tessellations of the Hyperbolic Plane«. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. Zv. 278, št. 1373. str. 147–167. ISSN 0080-4630.
Viri[uredi | uredi kodo]
- Chen, Zhibo; Liang, Tian (2006), »The converse of Viviani's theorem«, The College Mathematics Journal, 37 (5): 390–391
- Coxeter, Harold Scott MacDonald (1999), »Poglavje 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues, Proceedings of the London Mathematics Society, Ser. 2, Vol 43, 1937«, The Beauty of Geometry: Twelve Essays, Dover Publications, ISBN 0-486-40919-8
Zunanje povezave[uredi | uredi kodo]











































































































































































