Augustin Louis Cauchy
| Augustin Louis Cauchy | |
|---|---|
 Augustin Louis Cauchy, okoli 1840, litografija Zéphirin Belliard po sliki Jeana Rollerja. | |
| Rojstvo | 21. avgust 1789[1][2][…] Pariz[4] |
| Smrt | 23. maj 1857[5][1][…] (67 let) Sceaux[d][4] |
| Druga imena | Augustin-Louis Cauchy |
| Bivališče | |
| Državljanstvo | francosko |
| Narodnost | |
| Področja | matematika, mehanika, teorija elastičnosti |
| Ustanove | École Centrale du Panthéon École nationale des ponts et chaussées École Polytechnique |
| Alma mater | École nationale des ponts et chaussées |
| Doktorski študenti | Viktor Jakovljevič Bunjakovski (1825) Francesco Faà di Bruno (1856) |
| Poznan po | Cauchy-Riemannovi diferencialni enačbi Cauchyjev integralski izrek Cauchyjev napetostni tenzor Cauchyjeva porazdelitev Cauchyjeve integralske formule Cauchyjevo število Cauchyjevo zaporedje izrek o residuih neenakost Cauchyja-Bunjakovskega |
| Zakonec | Aloise de Bure |
| Otroci | Marie Françoise Alicia (1819) Marie Mathilde (1823) |
| Podpis | |
Baron Augustin Louis Cauchy [ožistén luí koší], francoski inženir in matematik, * 21. avgust 1789, Pariz, Francija, † 23. maj 1857, Sceaux, Seine, Francija.
Cauchy je eden od zgodnjih pionirjev matematične analize. Začel je projekt formuliranja in dokazovanja izrekov infinitezimalnega računa v strogem smislu in zavračal hevristično načelo splošnosti algebre, ki so jo izkoriščali predhodni avtorji. Postavil je temelje sodobni obravnavi konvergence, razvil kriterije za konvergenco neskončnih vrst in izdal tolmač infinitezimalnega računa na podlagi limite funkcije. Pri tem ni bil popolnoma uspešen, ker še ni imel konstrukcij iracionalnih števil, ki so jih kasneje razvili Cantor, Dedekind in Weierstrass.
Skoraj samostojno je osnoval kompleksno analizo in vpeljal raziskovanje permutacijskih grup v abstraktni algebri. S svojih globokim delom v matematiki je vplival na svoje sodobnike in naslednike. Njegova dela pokrivajo celotni obseg tedanje matematike in matematične fizike.
Po njem so poimenovali največ konceptov, pojmov in izrekov od vseh matematikov.[7] V teoriji elastičnosti se po njem imenuje šestnajst konceptov, pojmov in izrekov. Bil je plodovit pisec. Napisal je približno osemsto raziskovalnih člankov in pet učbenikov. Bil je pobožni rimskokatolik, izrecni bourbonski rojalist in tesno povezan z jezuitskim redom.
Bil je učenec in pozneje profesor na Politehniški šoli (EP) v Parizu, po revoluciji 1830 pa je kot izseljenec delal v Torinu in Pragi, dokler se ni vrnil na svoje mesto v Francijo. Bil je zaslužni profesor hkrati na École Polytechnique, Univerzi v Parizu in Francoskem kolegiju (College de France). Bil je med prvimi matematiki, ki so se zavedali moči objavljenih del. Njegovi učbeniki in izvirni prispevki so vnesli novo pojmovanje strogosti v diferencialni račun, iz katerega se je izoblikovalo področje matematične analize. Veliko je prispeval k razvoju splošne teorije funkcij. Z integralskimi izreki in uvedbo residuov je bistveno vplival na razvoj teorije kompleksnih funkcij. Izpopolnil je metode integriranja linearnih diferencialnih enačb. Leta 1822 je postavil temelje teorije elastičnosti, leta 1845 pa je bistveno prispeval k osnovam teorije grup. Med letoma 1844 in 1846 je začel objavljati svoja dela s tega področja. Pomemben je tudi za astronomijo, optiko in hidrodinamiko.
Dokazal je obstoj rekurentnih eliptičnih funkcij. Prvi je uporabil izraz determinanta.
Življenje[uredi | uredi kodo]
Mladost in izobrazba[uredi | uredi kodo]
Cauchy je bil sin Louisa Françoisa Cauchyja (1760–1848) in Marie-Madeleine Desestre. Imel je dva brata, Alexandra Laurenta Cauchyja (1792–1857), ki je leta 1847 postal predsednik oddelka prizivnega sodišča, leta 1849 pa sodnik kasacijskega sodišča; ter Eugena Françoisa Cauchyja (1802–1877), publicista, ki je tudi napisal več matematičnih del.
Leta 1818 se je poročil z Aloise de Bure. Bila je bližnja sorodnica založnika, ki je objavil večino njegovih del. Imela sta dve hčeri: Marie Françoise Alicia (1819) in Marie Mathilde (1823).
Njegov oče Louis François je bil visoki uradnik v pariški policiji nove ureditve. Zaradi francoske revolucije 14. julija 1789, ki je izbruhnila mesec dni pred Augustin Louisovim rojstvom, je izgubil službeno mesto.[a] Cauchyjeva družina je preživela revolucijo in prihajajočo vladavino terorja jakobinske diktature (1794). Prebežala je v Arcueil, kjer ga je začel poučevati oče. Po usmrtitvi Robespierra 28. julija 1794 so se lahko vrnili v Pariz. Tu je oče našel novo uradniško službo in kmalu napredoval. Ko je leta 1799 na oblast prišel Napoleon, je oče še bolj napredoval in postal glavni tajnik senata, ter delal neposredno pod Laplaceom (sedaj veliko bolj znanim po svojem delu iz matematične fizike). Tudi Lagrange je bil prijatelj družine.
Po Lagrageevem nasvetu se je Augustin Louis jeseni 1802 vpisal na École Centrale du Panthéon, tedaj najboljšo srednjo šolo v Parizu. Veliko predmetov je bilo klasičnih jezikov. Mladi in prizadevni Cauchy je bil sijajni dijak in je prejel več nagrad v latinščini in humanističnih predmetih. Navkljub tem uspehom je izbral inženirsko pot in se začel pripravljati na sprejemni izpit na École Polytechnique. Leta 1805 je bil na izpitu od 293 rijavljenih drugi, tako da so ga sprejeli. Eden od glavnih namenov te šole je bila priprava civilnih in vojaških inženirjev na nivoju visokošolske znanstvene in matematične izobrazbe. Delovala je pod vojaškim strogim redom, kar je mlademu in pobožnemu Cauchyju povzročalo težave pri prilagajanju. V starosti 18 let je končal politehniško šolo in se vpisal na École nationale des ponts et chaussées (Nacionalna šola za mostove in ceste). Diplomiral je iz gradbeništva nizkih gradenj z najvišjimi ocenami.
Inženirska leta[uredi | uredi kodo]
Po diplomi leta 1810 je sprejel službo kot mladi inženir v Cherbourgu, kjer je Napoleon želel zgraditi pomorsko oporišče. Tu je Cauchy ostal tri leta in, čeprav je imel zelo zasedeno upravljalno službo, je še vedno našel čas za pipravo treh matematičnih rokopisov, ki jih je predlagal v Première Classe (prvi razred) Francoskega inštituta (Institut de France).[b] Njegova prva dva rokopisa o pravilnih poliedrih so sprejeli, tretjega o stožnicah pa so zavrnili. Leta 1812 je podal popolni seznam Kepler-Poinsotovih poliedrov.
Septembra 1812 je zaradi prenapornega dela zbolel in se vrnil v Pariz. Drugi razlog za vrnitev v prestolnico je bil, ker je izgubil svoje zanimanje za inženirsko službo. Vedno bolj ga je privlačevala abstraktna lepota matematike. V Parizu je imel več možnosti, da bi na našel službo povezano z matematiko. Čeprav je formalno obdržal svojo inženirsvo službo, so ga s plačilnega seznama Ministrstva za pomorstvo prestavili na seznam Ministrstva za notranje zadeve. Naslednja tri leta je bil v glavnem na neplačanem bolniškem dopustu in se uspešno ukvarjal z matematiko, s povezanimi temami o simetričnih funkcijah, simetrični grupi in teoriji o algebrskih enačbah višjega reda. Med letoma 1813 in 1815 je poskušal postati član Prvega razreda Francoskega inštituta, vendar v treh različnih prilikah neuspešno. Leta 1815 so pri Waterlooju premagali Napoleona, na novo nameščeni bourbonski kralj Ludvik XVIII. pa je prevzel vzpostavitev vladanja. Akademijo znanosti so ponovno ustanovili marca 1816. Carnot in Monge sta zaradi politike izgubila članstvo v Akademiji, kralj pa je namesto njiju imenoval Cauchyja. Odpor drugih članov je bil oster. Menili so, da je njegov sprejem za članstvo Akademije sramota, Cauchy pa je zaradi tega v znanstvenih krogih pridobil veliko sovražnikov.
Profesor na École Polytechnique[uredi | uredi kodo]
Novembra 1815 je Poinsot, ki je bil izredni profesor na École Polytechnique, zaradi zdravstvenih razlogov zaprosil za izvzetost od poučevalskih dolžnosti. Cauchy je do tedaj že postal znani matematik in bi si zaslužil profesorsko mesto. Eden od njegovih velikih uspehov do tedaj je bil dokaz de Fermatovega izreka o mnogokotniških številih v splošnem. Ker je bil zelo zvest Bourbonom, je to nedvomno prispevalo k temu, da je nasledil Poinsota. Končno je opustil svojo inženirsko službo in prejel enoletno pogodbo za poučevanje matematike drugega letnika École Polytechnique. Leta 1816 so to bonapartistično, nereligiozno šolo prenovili, več liberalnih profesorjev pa so odpustili. Reakcionarnega Cauchyja so povišali v rednega profesorja.
V svojem 28-em letu je Cauchy še vedno živel pri starših. Za očeta je bil že skrajni čas, da se poroči. Cauchy se je zaročil z Aloïse de Bure. Člani družine de Bure so bili tiskarji in prodajalci knjig. Objavili so večino njegovih del.[8]:9 Aloïse in Augustin Louis sta se poročila 4. aprila 1818 v Cerkvi svetega Sulpicija v Parizu z veliko rimskokatoliško svečanostjo in obredom. Leta 1819 se jima je rodila prva hči Marie Françoise Alicia, leta 1823 pa druga in zadnja Marie Mathilde.[9]:134
Nazadnjaško politično ozračje, ki je trajalo do leta 1830, je Cauchyju popolnoma ustrezalo. Leta 1824 je umrl Ludvik XVIII., nasledil pa ga je še bolj nazadnjaški brat Karel X.. V tem času je bil Cauchy nadvse ustvarjalen in je objavljal pomembne matematične razprave eno za drugo. Dodelili so mu navskrižni delovni mesti na Francoskem kolegiju in na Faculté des Sciences tedanje Imperialne univerze.
V izgnanstvu[uredi | uredi kodo]
Julija 1830 se je v Franciji zgodila druga revolucija. Karel X. je pobegnil iz države, nasledil pa ga je nebourbonski kralj Ludvik Filip I. (Orléanski). Nemiri, v katerih so sodelovali uniformirani študenti École Polytechnique, so divjali blizu Cauchyjevega doma v Parizu.
Ti dogodki so zaznamovali preokretnico v njegovem življenju in prekinili njegovo matematično ustvarjalnost. Pretresen zaradi padca vlade je globoko zasovražil liberalce, ki so prevzeli oblast, in zapustil Pariz. Odšel je v tujino in za seboj pustil družino. Kratek čas je bil v Fribourgu v Švici, kjer se je moral odločiti ali bo zaprisegel zahtevano prisego zvestobe novemu režimu. To je zavrnil in zaradi tega je izgubil vsa delovna mesta v Parizu, razen svojega članstva v Akademiji, za katerega zaprisega ni bila potrebna. Leta 1831 je odšel v Torino. Po nekaj časa tamkajšnjega bivanja je sprejel ponudbo sardinijskega kralja, ki je tedaj vladal Torinu in sosednji pokrajini Piemont, za predstojnika stolice za teoretično fiziko, ki so jo ustanovili posebej zanj. V Torinu je poučeval v letih 1832 in 1833. Leta 1831 so ga izbrali za tujega člana Kraljeve švedske akademije znanosti.
Avgusta 1833 je zapustil Torino in odšel v Prago, kjer je postal zasebni učitelj 13-letnega vojvode Bordeauxa Henrija d'Artoisa (1820–1883), izgnanega kronskega princa in vnuka Karla X. Kot profesor École Polytechnique je bil Cauchy razvpito slab predavatelj in je zahteval nivo znanja, ki so ga lahko dosegli le nekateri najboljši, svoj odmerjeni čas predavanj pa je natrpal s preveč snovi. Mladi vojvoda ni imel ne okusa niti nadarjenosti za matematiko ali znanost, tako da si kot učenec in učitelj sploh nista ustrezala. Čeprav je Cauchy svojo nalogo vzel zelo resno, jo je opravljal z veliko okornostjo in s presenečeno pomanjkljivo veljavo nad mladim vojvodo.
Med svojim delovanjem kot gradbenik nizkih gradenj je bil za kratek čas vodja popravil nekaterih pariških odvodnih cestnih kanalov. Naredil je napako in je to povedal svojemu učencu. Z veliko zlobo je mladi vojvoda začel govoriti naokrog, da je gospod Cauchy začel svojo pot v pariških kanalih. Cauchy je bil zasebni učitelj do septembra 1838, ko je vojvoda napolnil 18 let. V teh petih letih je komajda kaj raziskoval, vojvoda pa je za celo življenje zasovražil matematiko. Edina dobra stvar, ki je izšla iz tega doživljaja, je bilo povzdignenje Cauchyja v barona, častni naziv, ki ga je zelo cenil. Leta 1834 sta se mu v Pragi pridružile žena in hčeri. Po štirih letih izgnanstva je bila njegova družina spet skupaj.
Zadnja leta[uredi | uredi kodo]
Pozno leta 1838 se je vrnil v Pariz in na svoje delovno mesto v Akademiji znanosti. Svojih profesorskih mest ni uspel spet pridobiti, ker je še vedno odklanjal prisego zvestobi. Vendar je še vedno obupno želel pridobiti formalni položaj v pariški znanstveni srenji.

Avgusta 1839 se je prosto delovno mesto pojavilo v Uradu za dolžine (Bureau des longitudes). Urad je bil podoben Akademiji. Imel je na primer pravico pritegniti svoje člane. Verjeli so, da so člani Urada lahko »pozabili« na prisego zvestobi, čeprav so bili formalno, za razliko od akademikov, obvezani nanjo. Urad je bil organizacija ustanovljena leta 1795 za rešitev problema določevanja lege na morju – večinoma zemljepisne dolžine, saj se lahko zemljepisna širina preprosto določa iz navidezne lege Sonca na nebu. Ker so dognali, da se lega na morju najboljše določa z astronomskimi opazovanji, se je Urad razvil v organizacijo, ki je spominjala na akademijo astronomskih znanosti.
Novembra 1839 so Cauchyja izvolili v Urad in kmalu je ugotovil, da zadeve s prisego ni bilo moč tako lahko odpraviti. Brez zaprisege je kralj zavrnil odobriti njegov izbor. Štiri leta je bil Cauchy v nesmiselnem položaju, da je bil izbran, ni pa mu to bilo odobreno. Zaradi tega formalno ni bil član Urada, ni prejemal plačila, ni mogel prisostvovati srečanjem in ni mogel predložiti člankov. Še vedno je odklanjal zaprisego, vendar se je počutil dovolj zvestega, da je usmeril svoje raziskovanje v nebesno mehaniko. Leta 1840 je Akademiji predstavil ducat člankov o tej temi. Opisal in ponazoril je tudi reprezentacijo števil s predznačeno števko, modificirani desetiški sistem, ki ga je v Angliji leta 1727 prikazal Colson. Zmešano članstvo v Uradu je za Cauchyja trajalo do leta 1843, ko ga je končno nasledil Poinsot.
Skozi celotno 19. stoletje se je francoski izobraževalni sistem bojeval z vprašanjem delitve cerkve in države. Rimskokatoliška cerkev si je prizadevala za svobodo izobrazbe. V Cauchyju je pri tem prizadevanju našla čvrstega in slavnega zaveznika. Svoj ugled in znanje je posodil École Normale Écclésiastique, šoli v Parizu, ki so jo vodili jezuiti, za vzgojo učiteljev v svojih kolegijih. Sodeloval je tudi pri ustanovitvi Katoliškega inštituta (Institut Catholique) v Parizu. Namen tega inštituta je bilo odvračanje posledic odsotnosti katoliškega univerzitetnega izobraževanja v Franciji. Te dejavnosti Cauchyja niso proslavile pri njegovih kolegih, ki so v celoti gledano, podpirali ideale razsvetljenstva francoske revolucije. Ko se je leta 1843 izpraznilo mesto stolice za matematiko na Francoskem kolegiju, je Cauchy zaprosil zanj, vendar je dobil le tri od 45-ih glasov.
Leto 1848 je bilo leto revolucij po vsej Evropi. Revolucije so izbruhnile v številnih državah, začele pa so se v Franciji. Kralj Ludvik Filip I., ki se je zbal enake usode Ludvika XVI., je pobegnil v Anglijo. Prisego zvestobi so odpravili in pot k akademskemu imenovanju je bila za Cauchyja končno prosta. 1. marca 1849 so ga ponovno imenovali za profesorja matematične astronomije na Faculté de Sciences Imperialne univerze Francije. Po njegovi smrti ga je na tej stolici nasledil Victor Puiseux.
Po političnem uporu skozi celo leto 1848 je Francija izbrala postati republika, pod predsedovanjem Louisa Napoléona Bonaparteja, Napoléonovega nečaka in sina Napoléonovega brata, ki so ga namestili za prvega kralja Holandije. Kmalu zgodaj leta 1852 je predsednik postal francoski cesar in prevzel ime Napoléon III.
Ne nepričakovano se je v uradniških krogih pojavila zamisel, da bi bilo koristno zahtevati zaprisego zvestobi od vseh državnih uslužbencev, vključno z univerzitetnimi profesorji. Zgodovina se ne ponavlja vedno, saj je sedaj lahko član kabineta prepričal imperatorja da izvzame Cauchyja od prisege. Cauchy je ostal profesor na Univerzi do svoje smrti v 67-em letu. Zadnje zakramente je prejel in umrl ob 4h ponoči 23. maja 1857.
Znanstveno delo[uredi | uredi kodo]
Zgodnje delo[uredi | uredi kodo]
Cauchyjeva nadarjenost se je razjasnila v njegovi preprosti rešitvi Apolonijevega problema o krožnici, ki se dotika treh danih krožnic, iz leta 1805, v njegovi posplošitvi Eulerjeve karakteristike za poliedre leta 1811 in v več drugih elegantnih problemih. Bolj pomembna je njegova razprava o širjenju valovanja za katero je leta 1816 prejel Veliko nagrado Francoske akademije znanosti. Njegovi zapisi so pokrivali pomembne teme, kot so: teorija vrst, kjer razvil pojem konvergence, in odkril veliko osnovnih formul za q-vrste. V teoriji števil in kompleksnih količin je prvi definiral kompleksna števila kot pare realnih števil. Pisal je tudi o teoriji grup in substitucijah, teoriji funkcij, diferencialnih enačbah in determinantah.
Mehanika, teorija elestičnosti[uredi | uredi kodo]
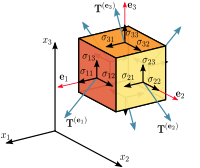
Pomembno je prispeval k mehaniki, kjer je zamenjal pojem zveznosti geometrijskega premika z načelom o zveznosti snovi. Pisal je o ravnovesju paličnih nosilcev in prožnih membranah, ter o valovanju v prožni snovi. Leta 1827 je uvedel simetrično matriko števil 3 × 3, sedaj znano kot Cauchyjev napetostni tenzor.[10] V teoriji elastičnosti je ustvaril teorijo o (mehanski) napetosti in njegovi rezultati so tako dragoceni kot Poissonovi. Cauchy je pojem mehanske napetosti v mehaniko kontinuumov uvedel okoli leta 1822. Matematično je tudi obdelal mehanske napetosti. V preprostem primeru je telo enoosno obremenjeno, na primer prizmatična palica z nateznimi ali tlačnimi napetostmi s silo, ki poteka skozi njeno (vzdolžno, glavno) os, tako da je napetost dana kot količnik sile in površine (začetnega) preseka palice po Hookovem zakonu:
V tem primeru je napetost podana kot skalar in se imenuje mehanska ali imenska napetost. Predstavlja povprečno vrednost napetosti po površini preseka, in je enakomerno porazdeljena. V splošnem pa napetost po preseku telesa ni enakomerno razporejena, tako da je napetost v točki dane površine različna od povprečne vrednosti napetosti po celotni površini. Po Cauchyju je napetost v poljubni točki v telesu, za katerega predpostavimo da je kontinuum – zvezno in nepretrgano sredstvo, popolnoma določena z devetimi komponentami simetričnega tenzorja ranga 2 , ki je znan kot Cauchyjev ali kartezični napetostni tenzor (tenzor napetosti):
kjer so , in normalne napetosti, , , , , in pa strižne napetosti. Prvi indeks naznačuje, da komponenta napetosti deluje na ravnino, ki je pravokotna na os , drugi indeks pa naznačuje smer v kateri deluje komponenta napetosti. Komponenta napetosti je pozitivna, če deluje v pozitivni smeri koordinatnih osi, in če ima ravnina, v kateri deluje, normalni vektor, ki kaže navzven v pozitivni koordinatni smeri. Po statično ravnovesnem stanju navorov vseh zunanjih sil med strižnimi napetostmi veljajo enakosti:
zato je le šest med seboj neodvisnih komponent: tri normalne napetosti (, , ) in tri strižne (, , ), Cauchyjev napetostni tenzor pa je zato simetričen:
Za Cauchyjev napetostni tenzor veljajo tenzorske transformacije pri spremembah koordinatnega sistema. Uporablja se pri telesih, ki se deformirajo v majhni meri. Za večje deformacije so potrebni drugi pokazatelji napetosti, na primer: prvi in drugi Piola-Kirchhoffov, Biotov in Kirchhoffov napetostni tenzor.
Optika, valovna teorija[uredi | uredi kodo]
V teoriji svetlobe je raziskoval Fresnelovo valovno teorijo, disperzijo in polarizacijo svetlobe.
Leta 1836 je zapisal Cauchyjevo enačbo, empirično povezavo med lomnim količnikom in valovno dolžino svetlobe za določeno prosojno snov.[11] V splošnem ima obliko:
kjer je n lomni količnik, λ valovna dolžina, , , , ..., koeficienti, po navadi podani za λ kot valovna dolžina vakuuma v mikrometrih. Običajno sta dovolj prva dva člena in koeficienta , .
Teorija števil[uredi | uredi kodo]
Prvi je leta 1818 v splošnem dokazal Fermatov izrek o mnogokotniških številih iz leta 1638.[12]:188 Za kvadratna števila ga je leta 1770 dokazal Lagrange, za trikotniška števila pa leta 1796 Gauss.
Kompleksne funkcije[uredi | uredi kodo]
Cauchy je najbolj znan po samostojnem razvitju teorije kompleksnih funkcij. Osrednji izrek, ki ga je dokazal, in se sedaj imenuje Cauchyjev integralski izrek, je:
kjer je kompleksna funkcija holomorfna na in znotraj nesamosekajoče sklenjene krivulje (konture), ki leži v kompleksni ravnini. Krivuljni integral poteka vzdolž konture . Zametki tega izreka se lahko zasledijo v članku, ki ga je 24 letni Cauchy predložil Akademiji znanosti (tedaj še vedno imenovani »Prvi razred Inštituta«) 11. avgusta 1814. Polno obliko izreka je predložil Akademiji 28. februarja 1825.[13] Ta članek imajo mnogi za njegov najpomembnejši dosežek v matematiki.
Leta 1826 je Cauchy dal formalno definicijo residua funkcije.[14] Ta pojem obravnava funkcije, ki imajo pole — izolirane singularnosti, točke, kjer gre funkcija k positivni ali negativni neskončnosti. Če se lahko kompleksna funkcija razvije v okolici singularnosti kot:
kjer je analitična (brez singularnosti), potem ima pol stopnje (reda) v točki . Če je , se pol imenuje enostavni pol. Koeficient je Cauchy imenoval residuum funkcije v točki . Če je v točki nesingularna, je residuum funkcije v točki enak nič. V enostavnem polu je residuum enak:
kjer je zamenjan s sodobnim zapisom residua.
Leta 1831, ko je bil v Torinu, je tamkajšnji Akademiji znanosti predložil dva članka. V prvem je predlagal formule, ki so sedaj znane kot Cauchyjeve integralske formule (Cauchyjevi obrazci):[15]
kjer je analitična na in znotraj območja, ki ga omejuje kontrura , v tem območju pa je včasih kompleksno število . Konturni integral poteka nasprotno smeri urinih kazalcev. Integrand ima enostavni pol v . V drugem članku je predstavil izrek o residuih:[16]
kjer vsota poteka po vseh polih in znotraj kontrure . Ti Cauchyjevi rezultati še vedno tvorijo jedro teorije kompleksnih funkcij, ki jo poučujejo fizikom in elektroinženirjem. Nekaj časa so Cauchyjevi sodobniki prezirali njegovo teorijo, ker so verjeli, da je prezapletena. Šele v 1940-ih so se odzvali nanjo, Laurent pa je bil prvi matematik poleg Cauchyja, ki je bistveno prispeval k njej (njegova Laurentova vrsta objavljena leta 1843).
Cours d'Analyse[uredi | uredi kodo]

Poleg svojega dela o kompleksnih funkcijah je bil Cauchy prvi, ki je poudarjal pomembnost strogosti v analizi. Njegova knjiga Tečaj analize (Cours d'Analyse) iz leta 1821 je imela takšen vpliv, da je Judith Victor Grabiner zapisala, »da je bil Cauchy mož, ki je učil strogo analizo celo Evropo.»[17] Knjigo večkrat navajajo kot prvi kraj, kjer so bili neenakosti in argumenti prvič predstavljeni v infinitazimalni račun. Michael Barany trdi, da je École pridobila pooblastilo nad vključitvijo infinitezimalnih metod nasproti Cauchyjevemu boljšemu razumevanju.[18] Gilain je razpravljal, da so infinitezimalni deli knjige verjetno kasnejši vstavek.[19] Laugwitz in Benis-Sinaceur sta menila, da Cauchyju ni bilo treba predavati infinitezimal, in pokazala, da jih je uporabljal v svojem lastnem delu vse do leta 1853.[20][21]
Cauchy je podal definicijo infinitezimale kot zaporedje, ki teži k nič. Napisali so veliko del o Cauchyjevem pojmu »infinitezimalno majhnih količinah«, in razpravljali, da vodijo od vsega iz običajnih »epsilonskih« definicij ali k pojmom nestandardne analize. Splošno mnenje je, da je Cauchy prezrl ali izpustil pomembne zamisli, da bi razjasnil točni pomen neskončno majhni količin, ki jih je uporabljal.[22]
Taylorjev izrek[uredi | uredi kodo]
Cauchy je prvi strogo dokazal Taylorjev izrek iz leta 1712 in uvedel svojo dobro znano obliko ostanka. Za svoje študente na École Polytechnique je napisal učbenik, v katerem je razvil osnovne izreke matematične analize v strogem smislu kot se je le dalo.[23] V tej knjigi je dal potrebni in zadostni pogoj za obstoj limite v obliki, ki jo še danes poučujejo. Tudi dobro znani kriterij absolutne konvergence izhaja iz te knjige – Cauchyjev kondenzacijski kriterij. Leta 1829 je prvič definiral kompleksno funkcijo kompleksne spremenljivke v drugem učbeniku.[24] Cauchyjevi lastni raziskovalni članki so navkljub temu vsebovali intuitivne in nestroge metode.[25]:176 Enega od njih je na primer s »protiprimerom« izpostavil Abel, ki se je kasneje popravil z uvedbo pojma enakomerne zveznosti.
Načelo argumenta, stabilnost[uredi | uredi kodo]
Dve leti pred smrtjo je leta 1855 objavil članek v katerem je obravnaval več izrekov, od katerih je eden podoben »načelu argumenta« iz mnogih sodobnih učbenikov o kompleksni analizi. V sodobnih učbenikih teorije upravljanja se Cauchyjevo načelo argumenta pogosto rabi za izpeljavo Nyquistovega kriterija stabilnosti, ki se lahko uporabi za napovedovanje stabilnosti ojačevalnika z negativno povratno zanko in kontrolnih sistemov z negativno povratno zanko. To Cauchyjevo delo je imelo močan vpliv tako na čisto kot na uporabno matematiko v inženirstvu.
Izbrana dela[uredi | uredi kodo]

Cauchy je bil zelo ustvarjalen. Po številu člankov ga je prekašal le Euler. Trajalo je skoraj stoletje, da so zbrali vse njegove zapise v 27 velikih knjig:
- Oeuvres complètes d'Augustin Cauchy publiées sous la direction scientifique de l'Académie des sciences et sous les auspices de M. le ministre de l'Instruction publique (27 knjig) (Pariz : Gauthier-Villars et fils, 1882–1974)
Njegove največje dosežke v matematični znanosti obdajajo stroge metode, ki jih je vpeljal. Vključene so v glavnem v njegovih treh velikih razpravah:
- Cours d'analyse de l'École royale polytechnique (1821)
- Le Calcul infinitésimal (1823)
- Leçons sur les applications de calcul infinitésimal; La géométrie (1826–1828)
Francoska akademija znanosti je zaradi njegove velike ustvarjalnosti v svoji publikaciji Comptes rendus omejila dolžino člankov na štiri strani, kar je v veljavi še sedaj.
Druga njegova dela so:
- Exercices d'analyse et de physique mathematique (Volume 1)
- Exercices d'analyse et de physique mathematique (Volume 2)
- Exercices d'analyse et de physique mathematique (Volume 3)
- Exercices d'analyse et de physique mathematique (Volume 4) (Pariz: Bachelier, 1840–1847)
- Analyse algèbrique (Imprimerie Royale, 1821)
- Nouveaux exercices de mathématiques (Pariz: Gauthier-Villars, 1895)
- Tečaji mehanike (za École Polytechnique)
- Višja algebra (za Faculté des Sciences)
- Matematična fizika (za Francoski kolegij).
- Mémoire sur l'emploi des equations symboliques dans le calcul infinitésimal et dans le calcul aux différences finis CR Ac ad. Sci. Paris, t. XVII, 449–458 (1843) velja za začetek operacijskega računa.
Politika in verska prepričanja[uredi | uredi kodo]
Cauchy je odraščal v hiši neomajnega rojalista. Zaradi tega je moral njegov oče med francosko revolucijo pobegniti v Arcueil. Njihovo tamkajšnje življenje je bilo očitno težko. Oče je govoril, da so v tem času živeli od riža, kruha in keksov. Odstavek iz njegovega nedatiranega pisma materi v Rouen navaja:[26]:13
Nikoli nismo imeli več kot polovice funta kruha in včasih niti toliko. To smo dopolnili z majhno dobavo trdih keksov in riža, ki so nam jo dodelili. Drugače nam gre precej dobro, kar je pomembno in kaže na to, da lahko ljudje preživijo z malim. Moram ti povedati, da imam za otroško kašo še vedno malo gladke bele moke od pšenice, ki sem jo vzgojil na svoji lastni zemlji. Imel sem jo 3 mernike [pribl. 90 l], imam pa tudi nekaj funtov krompirjevega škroba. Je bel kot sneg in tudi zelo dober, še posebno za zelo mlade otroke. Tudi škrob sem vzgojil na svoji lastni zemlji.[27]
Cauchy je vsekakor podedoval očetov neomajni rojalizem in je zaradi tega po padcu Karla X. zavračal prisege vsakršni vladi.
Podobno je bil neomajni rimskokatolik in član Družbe svetega Vincencija de Paula.[28] Bil je povezan tudi z jezuiti in jih branil pri Akademiji, ko politično to ni bilo modro. Njegova gorečnost za svojo vero ga je vodila pri skrbi za Hermita, ki se je leta 1856 nalezel koz, in z njegovim vodstvom postal verni katolik. Vodila ga je tudi pri branjenju Irske med krompirjevo lakoto.
Njegov rojalizem in vnema sta ga naredila tudi prepirljivega, kar je pri kolegih povzročalo težave. Čutil je, da so grdo ravnali z njim zaradi svojih prepričanj, njegovi nasprotniki pa so menili, da je namenoma izzival ljudi in jih grajal zaradi verskih prepričanj ali branil jezuite potem, ko so jih zatrli. Abel ga je imenoval »pobožnjakarski katolik«.[29]:273 in dodal, da »je bil nor in, da se ne more zanj narediti nič,« na drugi strani pa ga je hvalil kot matematika. Cauchyjevi pogledi so bili med matematiki na široko nepriljubljeni in, ko je pred njim stolico za matematiko prevzel Libri Carucci dalla Sommaja, je skupaj z drugim menil, da so krivi Cauchyjevi pogledi. Ko so Librija obsodili kraje starodavnih in dragocenih rokopisov in knjig, ga je nasledil Liouville, kar je med njim in Cauchyjem povzročilo nesoglasja. Drugi spor je zadeval Duhamela in njegovega lastninjenja pravice do odkritja neelastičnih udarov. Kasneje je Poncelet pokazal, da se je Cauchy motil.
Priznanja[uredi | uredi kodo]
Njegovo ime je vgrajeno med 72-imi pomebnimi francoskimi znanstveniki okrog prvega nadstropja Eifflovega stolpa.
Poimenovanja[uredi | uredi kodo]

Po njem se imenuje udarni krater Cauchy na Luni in asteroid glavnega pasu 16249 Cauchy, ki ga je odkril Comba 29. aprila 2000 v Prescottu, Arizona.
Glej tudi[uredi | uredi kodo]
- Cauchy-Binetova formula
- Cauchy-Eulerjeva enačba
- Cauchyjev indeks
- Cauchyjev kriterij
- Cauchyjev problem
- Cauchyjev produkt
- Cauchyjeva funkcionalna enačba
- Cauchyjeva glavna vrednost
- Cauchyjeva matrika
- Cauchyjevo obzorje
- izrek Cauchyja in Kovalevske
- Peanov eksistenčni izrek (Cauchy-Peanov izrek)
- Picard-Lindelöfov izrek (Cauchy-Lipschitzev izrek)
Opombe[uredi | uredi kodo]
- ↑ Očetova odpustitev velja za vzrok globokega sovraštva do francoske revolucije, ki jo je Cauchy čutil vse svoje življenje.
- ↑ V revolucionarnih dneh je bila Francoska akademija znanosti znana kot »Prvi razred« Francoskega inštituta.
Sklici[uredi | uredi kodo]
- ↑ 1,0 1,1 MacTutor History of Mathematics archive — 1994.
- ↑ podatkovna baza Léonore — ministère de la Culture.
- ↑ Record #11895590x // BnF catalogue général — Paris: BnF.
- ↑ 4,0 4,1 Коши Огюстен Луи // Большая советская энциклопедия: [в 30 т.] — 3-е изд. — Moskva: Советская энциклопедия, 1969.
- ↑ Record #118519735 // Gemeinsame Normdatei — 2012—2016.
- ↑ SNAC — 2010.
- ↑ Freudenthal (2008).
- ↑ Bradley; Sandifer (2009), str. 9.
- ↑ Belhoste (1991), str. 134.
- ↑ Cauchy (1827).
- ↑ Cauchy (1836).
- ↑ Heath (1910), str. 188.
- ↑ Cauchy (1825).
- ↑ Cauchy (1826).
- ↑ Cauchy (1831a).
- ↑ Cauchy (1831b).
- ↑ Grabiner (1981).
- ↑ Barany (2011).
- ↑ Gilain (1989).
- ↑ Laugwitz (1989).
- ↑ Benis-Sinaceur (1973).
- ↑ Barany (2013).
- ↑ Cauchy (1821).
- ↑ Cauchy (1829).
- ↑ Kline (1980), str. 176.
- ↑ Valson (1868), str. 13.
- ↑ Belhoste (1991), str. 3.
- ↑ »CATHOLIC ENCYCLOPEDIA: Augustin-Louis Cauchy« (v angleščini). Newadvent.org. 1. november 1908. Pridobljeno 19. junija 2009.
- ↑ Bell (1986), str. 273.
Viri[uredi | uredi kodo]
- Barany, Michael (2011). »God, king, and geometry: revisiting the introduction to Cauchy's Cours d'analyse«. Historia Mathematica. Zv. 38.
- Barany, Michael (2013). »Stuck in the Middle: Cauchy's Intermediate Value Theorem and the History of Analytic Rigor«. Notices of the American Mathematical Society. Zv. 60, št. 10. str. 1334–1338. doi:10.1090/noti1049.
- Belhoste, Bruno (1991). Augustin-Louis Cauchy: A Biography. Frank Ragland (prevod). Ann Arbor, Michigan: Springer-Verlag New York Inc. ISBN 3-540-97220-X.
- Bell, Eric Temple (1986). Men of Mathematics. Simon and Schuster. ISBN 9780671628185.
- Benis-Sinaceur, Hourya (1973). »Revue d'histoire des sciences«. Cauchy et Bolzano. Zv. Tome 26 n°2. str. 97–112.
- Bradley, Robert E.; Sandifer, C. Edward (2009). Cauchy's Cours d'analyse: An Annotated Translation. Springer. ISBN 1-4419-0548-0.
- Cauchy, Augustin Louis (1821). Cours d'Analyse de l'École Royale Polytechnique, I.re partie. Pariz: Analyse Algébrique.
- Cauchy, Augustin Louis (1825), Mémoire sur les intégrales définies prises entre des limites imaginaires [Zapis o določenih integralih med imaginarnimi limitami]
- Cauchy, Augustin Louis (1826). »Sur un nouveau genre de calcul analogue au calcul infinitésimal [O novi vrsti računa analognega infinitezimalnem računu]«. Exercices de Mathématique. Zv. 1. str. 11.
- Cauchy, Augustin Louis (1827). »De la pression ou tension dans un corps solide [O tlaku ali napetosti v trdnini]«. Exercices de Mathématiques. Zv. 2. str. 42.
- Cauchy, Augustin Louis (1829), Leçons sur le Calcul Différentiel, Pariz
- Cauchy, Augustin Louis (1831a), Sur la mécanique céleste et sur un nouveau calcul qui s'applique à un grande nombre de questions diverses [O nebesni mehaniki in o novem računu, ki se lahko uporabi v velikem številu mnogovrstnih vprašanj], predloženo Akademiji znanosti v Torinu 11. oktobra 1831
- Cauchy, Augustin Louis (1831b), Mémoire sur les rapports qui existent entre le calcul des Résidus et le calcul des Limites, et sur les avantages qu'offrent ces deux calculs dans la résolution des équations algébriques ou transcendantes [Zapis o povezavah, ki obstajajo med računom o residuih in računom o limitah, ter o prednostih, ki ga ta račun ponuja pri reševanju algebrskih in transcendentnih enačb], predloženo Akademiji znanosti v Torinu 27. novembra 1831
- Cauchy, Augustin Louis (1836). Mémoire sur la dispersion de la lumière. Praga: J.G. Calve.
- Gilain, C. (1989). »Cauchy et le Course d'Analyse de l'École Polytechnique«. Bulletin de la Société des amis de la Bibliothèque de l'École polytechnique. Zv. 5. str. 3–145.
- Grabiner, Judith Victor (1981). The Origins of Cauchy's Rigorous Calculus (PDF). Cambridge, MA.: The MIT press.
- Freudenthal, Hans (2008). »Cauchy, Augustin-Louis.«. V Gillispie, Charles (ur.). Dictionary of Scientific Biography (v angleščini). New York: Scribner & American Council of Learned Societies. ISBN 978-0-684-10114-9.
- Heath, Thomas Little (1910). Diophantus of Alexandria; a study in the history of Greek algebra. Cambridge University Press.
- Kline, Morris (1980). Mathematics: The Loss of Certainty. COBISS 8041561. ISBN 0-19-503085-0.
- Laugwitz, Detlef (1989). »Definite values of infinite sums: aspects of the foundations of infinitesimal analysis around 1820«. Arch. Hist. Exact Sci. Zv. 39, št. 3. str. 195–245. doi:10.1007/BF00329867.
- Valson, Claude Alphonse (1868). La Vie et les Travaux du baron Cauchy. Zv. 1. del. Pariz: Gauthier-Villars.
Nadaljnje branje[uredi | uredi kodo]
- Boyer, C. (1949). The concepts of the calculus. Hafner Publishing Company.
- Cauchy, Augustin Louis (1821). Cours d'analyse de l'Ecole Royale Polytechnique. Imprimerie royale. (ponatis Cambridge University Press, 2009; ISBN 978-1-108-00208-0)
- Cauchy, Augustin Louis (1882). Oeuvres completes. Gauthier-Villars. (ponatis Cambridge University Press, 2009; ISBN 978-1-108-00317-9)
Zunanje povezave[uredi | uredi kodo]
- Stran o Augustinu Louisu Cauchyju Univerze svetega Andreja (angleško)
- Cauchyjev kriterij konvergence Arhivirano 2005-06-17 na Wayback Machine. na PlanetMath (angleško)
- Œuvres complètes d'Augustin Cauchy Francoska akademija znanosti. Ministère de l'éducation nationale. (francosko)
- Augustin-Louis Cauchy – Œuvres complètes (v dveh delih) Gallica-Math (francosko)
- Augustin Louis Cauchy na Projektu Matematična genealogija (angleško)
- Hartshorne, Robin Cope, Augustin-Louis Cauchy – Cauchy's Life (angleško)
- Rassias, Th. M., Topics in Mathematical Analysis, A Volume Dedicated to the Memory of A. L. Cauchy, World Scientific Co., Singapore, New Jersey, London, 1989.
 Cauchy, Augustin Louis, New International Encyclopedia, 1905 (angleško)
Cauchy, Augustin Louis, New International Encyclopedia, 1905 (angleško)











































