Kepler-Poinsotov polieder
Kepler-Poinsotov polieder (tudi Kepler-Poinsotovo telo) je v geometriji katerikoli od štirih pravilnih steliranih poliedrov. Dobimo jih z steliranjem pravilnih konveksnih dodekaedrov in ikozaedrov. Od teh se razlikujejo v tem, da imajo pentagramske stranske ploskve ali slike oglišč.
Štirje Kepler-Poinsotovi poliedri so prikazani na zgornji sliki. Vsakega izmed njih lahko identificiramo s Schläflijevim simbolom v obliki {p, q} in njegovim imenom.
Značilnosti[uredi | uredi kodo]
Eulerjeva karakteristika[uredi | uredi kodo]
Kepler-Poinsotovi poliedri prekrivajo sfero več kot enkrat, tako da središča stranskih ploskev delujejo kot navite točke v sliki, ki imajo petkotne stranske ploskve in oglišča v drugih. Zaradi tega niso nujno topološko enakovredne sferi kot so platonska telesa. Odnos:
vedno ne velja. Po Schläfliju velja, da morajo imeti vsi poliedri χ = 2. On je tudi zavračal zamisel o tem, da sta mali stelirani dodekaeder in veliki dodekaeder prava poliedra, kar pa nikoli ni bilo splošno priznano.
Popravljeno obliko Eulerjeve karakteristike z uporabo gostote D pripadajočih slik oglišč dv in stranskih ploskev df je podal angleški matematik Arthur Cayley (1821 – 1895). Izraz velja za konveksne poliedre (kjer so faktorji popravkov vsi enaki 1) in za Kepler-Poinsotove poliedre:
Dualnost[uredi | uredi kodo]
Kepler-Poinsotovi poliedri nastopajo v dualnih parih.
Pregled[uredi | uredi kodo]
| ime | slika | sferno tlakovanje |
diagram stelacije |
Schläflijev {p,q} in Coxeter-Dinkinov diagram |
stranske ploskve {p} |
robovi | oglišča {q} slika oglišč |
χ | gostota | simetrija | dualni |
|---|---|---|---|---|---|---|---|---|---|---|---|
| mali stelirani dodekaeder | 
|

|

|
{5/2,5} |
12 {5/2} |
30 | 12 {5} |
-6 | 3 | Ih | veliki dodekaeder |
| veliki dodekaeder | 
|

|

|
{5,5/2} |
12 {5} |
30 | 12 {5/2} |
-6 | 3 | Ih | mali stelirani dodekaeder |
| veliki stelirani dodekaeder | 
|

|

|
{5/2,3} |
12 {5/2} |
30 | 20 {3} |
2 | 7 | Ih | veliki ikozaeder |
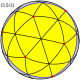
| veliki ikozaeder | 
|
|

|
{3,5/2} |
20 {3} |
30 | 12 {5/2} |
2 | 7 | Ih | veliki stelirani dodekaeder |
Odnosi med pravilnimi poliedri[uredi | uredi kodo]
| Naslednji imajo iste ureditve oglišča: | Naslednji imajo isto razvrstitev oglišč in razvrstitev robov: |
|---|---|
    ikozaeder, mali stelirani dodekaeder, veliki ikozaeder in veliki dodekaeder. |
  mali stelirani dodekaeder in veliki ikozaeder. |
  dodekeder in veliki stelirani dodekaeder. |
  ikozaeder in veliki dodekaeder. |
Glej tudi[uredi | uredi kodo]
- pravilni politop
- pravilni polieder
- uniformni polieder
- uniformni stelirani polieder
- poliederska sestava
- Schläfli-Hessov polihoron
Zunanje povezave[uredi | uredi kodo]
- Weisstein, Eric Wolfgang. »Kepler-Poinsot Solid«. MathWorld.
- Modeli Kepler-Poinsotovih teles (angleško)
- Uniformni poliedri (angleško)
- Kepler-Poinsotovi poliedri (angleško)
- Modeli Kepler-Poinsotovih poliedrov (angleško)
- Stella software za kreiranje slik (angleško)




