Antiprizma

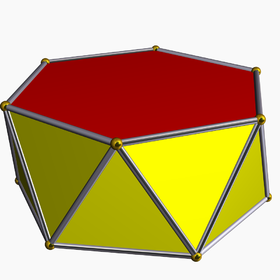
Množica uniformnih antiprizem
tip	uniformni polieder
stranske ploskve	2 n-kotniki, 2n trikotnikov
robovi	4n
oglišče	2n
konfiguracija oglišč	3.3.3.n
Schläflijev simbol	h0,1{2,2n} s{2,n}
Coxeter-Dynkinovi diagrami
grupa simetrije	Dnd, [2+,2n], (2*n), reda 4n Dn, [2,n]+, (22n), reda 2n
dualni polieder	trapezoeder
lastnosti	konveksni, polpravilni izogonalni
mreža

Antiprizma je v geometriji vzporedni polieder, ki ga sestavljata dve vzporedni kopiji istega n-stranskega mnokotnika, ki sta povezana s trakom izmeničnih trikotnikov. Takšno telo imenujemo n-stranska antiprizma.

Antiprizme spadajo v podrazred prizmatoidov.

Antiprizme so podobne prizmam razen v tem, da so osnovne ploskve zavrtene druga proti drugi in, da so stranske ploskve trikotniki in ne četverokotniki.

V primeru pravilne n-stranske osnove, se običajno obravnava primer, ko se kopija zavrti za kot 180°/n. Posebna pravilnost se doseže takrat, ko je črta, ki povezuje obe osnovni ploskvi, pravokotna na osnovno ploskev. V tem primeru dobimo pravokotno antiprizmo. Kot stranske ploskve ima n-kotne osnovne ploskve in za povezavo teh dveh osnovnih ploskev ima 2n enakostraničnih trikotnikov.

Uniformna antiprizma

Uniformna antiprizma ima razen osnovnih ploskev še 2n enakostraničnih trikotnikov kot stranske ploskve. Kot razred tvorijo antiprizme neskončno skupino ogliščno uniformnih poliedrov, prav tako kot uniformne prizme. Za n=2 dobimo degenerirani primer pravilnega tetraedra. Za n=3 pa nedegeneriran pravilni oktaeder.

Dualni poliedri antiprizme so trapezoedri (antidipiramide ali deltoedri). Njihov obstoj je prvi obravnaval in tudi skoval ime nemški astrolog, astronom in matematik Johannes Kepler (1571 – 1630).

Kartezične koordinate

Kartezične koordinate za oglišča pravokotne antiprizme z n-kotno osnovo in enakokrakimi trikotniki so

$\left( \cos\frac{k\pi}{n}, \sin\frac{k\pi}{n}, (-1)^k h \right)$

kjer se k spreminja od 0 do 2n-1. Kadar pa so trikotniki enakostranični, velja

$2h^2=\cos\frac{\pi}{n}-\cos\frac{2\pi}{n}$.

Prostornina in površina

Če je a dolžina roba uniformne antiprizme, potem je njena prostornina enaka:

$V = \frac{n \sqrt{4\cos^2\frac{\pi}{2n}-1}\sin \frac{3\pi}{2n} }{12\sin^2\frac{\pi}{n}} \; a^3$.

Površina pa je

$P = \frac{n}{2} ( \cot{\frac{\pi}{n}} + \sqrt{3}) a^2.$

Simetrija

Grupa simetrije pravokotne n-stranske antiprizme s pravilnima osnovnima ploskvama in enakokrakimi stranskimi ploskvami je D_nd reda 4n, razen v primeru tetraedra, ki pa ima ima višjo grupo simetrije T_d reda 24. Ta grupa simetrije ima tri verzije D_2d kot podgrupe. Isto velja tudi za oktaeder, ki pa ima simetrijsko grupo O_h reda 48, ki pa ima štiri oblike D_3d kot podgrupe.

Grupa simetrije vsebuje središčno simetrijo samo, če in samo, če je n neparen.

Grupa vrtenj je D_n reda 2n, razen za tetraeder, ki pa ima višjo grupo vrtenj T reda 12, ki pa ima tri oblike D₂ podgrup. To velja tudi za oktaeder, ki ima višjo grupo vrtenja O reda 24, ki pa ima štiri verzije D₃ kot podgrupe.

Glej tudi

• prizmatični uniformni polieder
• oktaeder
• kvadratna antiprizma
• petkotna antiprizma
• šestkotna antiprizma
• osemkotna antiprizma
• desetkotna antiprizma
• dvanajstkotna antiprizma
• apeirogonalna antiprizma
• velika antiprizma

Zunanje povezave

• Antiprizma na Mathworld (v angleščini)
• Nekoveksne prizme in antiprizme (v angleščini)
• Antiprizma v Glossary for Hyperspace (v angleščini)
• Prizme, antiprizme in njihovi duali (v angleščini)
• Prizmatični politopi v Glossary for Hyperspace (v angleščini)