Abstraktni politop

Abstraktni politop je v matematiki struktura – algebrska delno urejena množica, ki se obravnava kot kombinatorična oblika običajnega politopa, če se zanemari mnogo njegovih geometrijskih značilnosti kot so koti, dolžine robov itd. Izraz politop je posplošitev pojmov mnogokotnik in polieder na področje poljubnega števila razsežnosti. Vsak običajni geometrijski politop je realizacija v poljubnem realnem n-razsežnem prostoru, običajno evklidskem, odgovarjajočega abstraktnega politopa. Abstraktna definicija politopov dovoljuje nekaj splošnejših kombinatoričnih struktur od tradicionalne definicije, in tako dovoljuje mnogo novih objektov, ki v tradicionalni teoriji nimajo svojega dvojnika. Zato za vse abstrakne politope ne obstaja takšen evklidski prostor, ki bi jih moral vsebovati.
Običajni in abstraktni politop[uredi | uredi kodo]
V evklidski geometriji je zgornjih šest štirikotnikov popolnoma enakih (glej sliko na desni).
V teh primerih so povezave med elementi enake ne glede na fizični izgled povezav. Za takšne elemente velja, da so kombinatorično ekvivalentni. Ta ekvivalenca je vključena v sam pojem abstraktnega politopa. Zaradi tega so tudi vsi zgornji politopi enaki. Reče se tudi, da so izomorfni ali »strukturo ohranjajoči.«
Značilnosti, ki so merljive v običajnih politopih, kot so koti, dolžine robov, poševnost in konveksnost, pri abstraktnih politopih nimajo pomena. Drugi običajni pojmi se lahko uporabijo, vendar ne vedno na enak način. Poskrbeti je treba za to kaj velja za običajne politope, ki niso abstraktni. Zgled: običajni politop je pravilen, če so vse njegove facete in slike oglišč pravilne, kar za abstraktne politope ne velja.[1]
Definicija[uredi | uredi kodo]
Abstraktni politop je delno urejena množica, njeni elementi se imenujejo stranske ploskve, ki zadoščajo štirim aksiomom:
- imajo najmanjšo stransko ploskev in največjo stransko ploskev.
- vse zastave vsebujejo isto število stranskih ploskev.
- je strogo povezan.
- vsak 1-odrezek je odsek premice.
n-politop je politop z rangom n.
Osnovni pojmi[uredi | uredi kodo]
Politopi kot poseti[uredi | uredi kodo]
Politopi imajo razsežnostno hierahijo razen abstraktnih politopov. Tako imajo po vrsti oglišča, robovi in stranske ploskve razsežnosti 0, 1 in 2. Sama kocka pa je trirazsežna.
V abstraktni teoriji pojem ranga nadomešča pojem razsežnost. Tako imajo oglišča rang q in robovi rang 1.
Izraz stranska ploskev se uporablja za element poljubnega ranga, za oglišča z rangom 0 ter robov z rangom 1 in ne samo za stranske ploskve z rangom 2. Poljubni element z rangom k se imenuje k-stranska ploskev.
Lahko se definira politope kot množico stranskih ploskev P z relacijo ureditve <, ki zadošča določenim dodatnim aksiomom. Množica P se imenuje strogo delno urejena množica ali poset.
Kadar je F < G velja, da je F podstranska ploskev za G ali tudi G ima podstransko ploskev F.
Lahko se reče, da sta F in G incidentna, če je F = G ali F < G ali G < F.
Najmanjša in največja stranska ploskev[uredi | uredi kodo]
Podobno kot sta pojma ničle in neskončnosti nujna v matematiki, bi bilo koristno tudi, če bi vsak politop imel najmanjšo in največjo stransko ploskev. Najmanjša stranska ploskev bi bila podstranska ploskev vseh drugih stranskih ploskev. Največja stranska ploskev bi bila tista, ki je podstranska vseh ostalih.
V resnici ima politop samo eno stransko ploskev. V tem primeru pa bi bili obe isti.
Največja in najmanjša stranska ploskev se imenujeta tudi nelastni stranski ploskvi, vse druge pa se imenujejo lastne.
Najmanjša stranska ploskev se imenuje tudi ničelna stranska ploskev, ker nima oglišč kot podstranskih ploskev.
Preprosti zgled[uredi | uredi kodo]
| vrsta stranske ploskve | rang (k) | število | k-stranske ploskve |
|---|---|---|---|
| najmanjša | −1 | 1 | F−1 |
| oglišče | 0 | 4 | a, b, c, d |
| rob | 1 | 4 | W, X, Y, Z |
| največja | 2 | 1 | G |
Relacija < je določena kot množica parov, ki vključujejo
- F−1<a, ... , F−1<X, ... , F−1 < G, ... , b < Y, ... , c < G, ... , Z < G.
V tem primeru se lahko piše robove W, X, Y in Z kot ab, ad, bc in cd. Pogosto se uporablja ta zapis z oglišči, ki pa ni vedno primeren.
To se včasih imenuje tudi kvadratna in ne štirikotniška, ker v abstraktnem svetu ni kotov ne robov in njihovih dolžin. Vsi štirje robovi so enaki in geometrija v vsakem oglišču je ista.
Relacije reda so tranzitivne, če je F < G in G < H, kar določa, da je tudi F < H. Da bi se določalo hierarhijo stranskih ploskev, ni potrebno, da bi se uporabilo vse primere F < H. Dovolj je, da se uporabi enega, če je ta naslednik drugega. To pomeni tam, kjer je F < H in noben G ne zadošča pogoju F < G < H.
Hassejev diagram[uredi | uredi kodo]

Manjši poseti in politopi se pogosto najlažje prikažejo s pomočjo Hassejevega diagrama. Po dogovoru se stranske ploskve istega ranga prikažejo na istem navpičnem nivoju. Vsaka črta med stranskimi ploskvami označuje par F, G tako, da je F < G, kjer je F pod G v diagramu.
Politop se pogosto prikaže kot graf, obeh (Hassejevega diagrama in grafa) pa se ne sme enačiti. Graf ima oglišča in robove, nima pa drugih stranskih ploskev. V splošnem imajo lahko različni politopi tudi iste grafe. Za večino politopov za ostale stranske ploskve s pomočjo sklepanja ni možno dobiti iz grafa.
Razen tega Hassejev diagram popolnoma opisuje katerikoli poset. Vsa struktura je prikazana v Hassejevem diagramu. Izomorfni politopi se prikazujejo s Hassejevimi diagrami in obratno.
Rang[uredi | uredi kodo]
Rang stranske ploskve F je določen kot celo število (m - 2) , kjer je m največje število stranskih ploskev v poljubni verigi (F', F", ... , F) kjer je F' < F" < ... < F.
Rang delno urejene množice (poseta) P je maksimalni rang n poljubne stranske ploskve.
Najmanjša ploskev (nikakor pa nobena druga) ima rang -1. Največja stranska ploskev ima rang n . Pogosto se to označuje kot F-1 in Fn.
Rang stranske ploskve ali politopa običajno odgovarja razsežnosti za podobne pojme v tradicionalni teoriji, kar pa ni vedno res. Za zgled se pogleda stransko ploskev ranga 1, ki odgovarja robu, ki pa je enorazsežen. Toda poševni mnogokotnik je v običajni geometriji trirazsežen, ker ni raven. Njegov abstraktni ekvivalent in vsi abstraktni mnogokotniki pa imajo rang 2.
V naslednji preglednici so podani rangi za različne vrste stranskih ploskev:
| Rang | -1 | 0 | 1 | 2 | 3 | ... | n - 2 | n - 1 | n |
|---|---|---|---|---|---|---|---|---|---|
| vrsta stranske ploskve | najmanjša | oglišče | rob | † | celica | sedlo | faceta | največja |
Daljica[uredi | uredi kodo]
Daljica je poset, ki ima najmanjšo stransko ploskev oziroma dve 0-stranski ploskvi ter največjo stransko ploskev. Zgled: {ø, a, b, ab}. Sledi, da imata oglišči a in b rang 0 in da ima največja stranska ploskev ab (poset) rang enak 1.
Zastave[uredi | uredi kodo]
Zastava je največja veriga stranskih ploskev oziroma polno urejena množica Ψ.
Zgled:{ø, a, ab, abc} je zastava v trikotniku abc.
Dodatno zahtevamo še, da za dani politop, vse zastave vsebujejo isto število stranskih ploskev. Poseti v splošnem ne zadoščajo tej zahtevi. Zgled: poset {ø, a, b, bc, abc} ima 2 zastavi neenakih velikosti in tako ni politop.
Sekcije[uredi | uredi kodo]

Vsaka podmnožica P' poseta P je poset z isto relacijo < omejeno na P' .
Za dani stranski ploskvi F in H iz P za katero je F ≤ H se množica {G | F ≤ G ≤ H}imenuje sekcija za P in se jo označuje z H/F. V teoriji reda je sekcija zaprti interval poseta in se ga označuje z [F, H].
P je torej tudi sekcija.
Zgled: v prizmi abcxyz je sekcija xyz/ø (glej sliko na desni) (označena s svetlo zeleno) je trikotnik
- {ø, x, y, z, xy, xz, yz, xyz}.
K-sekcija je sekcija z rangom k.
Politop, ki je podmnožica drugega politopa, je vedno sekcija. Kvadrat abcd je podmnožica tetraedra abcd, ki pa ni njegova sekcija. Pojem sekcije nima istega pomena kot je v običajni geometriji.
Slike oglišč[uredi | uredi kodo]
Slika oglišč v danem oglišču V je (n−1)-sekcija Fn/V, kjer je Fn največja stranska ploskev.
Zgled: v trikotniku abc je slika oglišč pri b, abc/b je {b, ab, bc, abc}, kar pa je daljica. Slika oglišč kocke so trikotniki.
Povezljivost[uredi | uredi kodo]
Za poset P se reče, da je povezan, če ima rang ≤ 1 ali kadar za poljubni dve lastni stranski ploskvi F in G obstaja lastno zaporedje stranskih ploskev:
- H1, H2, ... ,Hk
tako, da je F = H1, G = Hk in za vsak Hi kjer je i < k, ki je incidenten svojemu nasledniku.
Zgornji pogoj zagotavlja, da par nepovezanih trikotnikov abc in xyz ni en politop.
Poset P je strogo povezan, če je vsaka sekcija P, vključno s P, povezana.
Z to dodatno zahtevo se dve piramidi s skupnim ogliščem izključujeta. Pri tem pa sta dve kvadratni piramidi lahko zlepljeni v njihovih kvadratnih stranskih ploskvah, kar da oktaeder. Skupna stranska ploskev pri tem ni stranska ploskev oktaedra.
Najenostavnejši politopi[uredi | uredi kodo]
Rang < 2[uredi | uredi kodo]
Obstaja samo po eden politop za vsak rang -1, 0 in 1. To so po vrsti ničelni politop, točka in daljica.
Za n ≤ 1 so vsi n-deli politopa n politopi. Stranske ploskve ranga 0 in 1 politopa se imenujejo oglišča in robovi.
Rang = 2[uredi | uredi kodo]
Za vsak p za katerega velja 3 ≤ p < je abstraktni ekvivalent tradicionalnega mnogokotnika s p oglišči in p robovi ali p-kotnik. Za p = 3, 4, 5,... je po vrsti trikotnik, kvadrat, petkotnik, ...
Za p = 2 je dvokotnik in za p = se dobi apeirogon.
Dvokotnik[uredi | uredi kodo]

Dvokotnik je mnogokotnik z dvema robovoma. V nasprotju z drugimi mnogokotniki imata oba roba isto oglišče. Zaradi tega se ga včasih obravnava kot izrojenega.
Za definicijo stranske ploskve se uporablja »ogliščni zapis.« To pomeni, da se za trikotnik abc zapiše {ø, a, b, c, ab, ac, bc, abc}. Ta način je boljši kot uporaba relacije <.
Uporaba dvokotnika ter mnogih drugih abstraktnih politopov onemogoča uporabo ogliščnega zapisa. Namesto tega je treba dati stranskim ploskvam imena in specificirati podstranskim parom F < G.
To pomeni, da se dvokotnik lahko definira kot množico {ø, a, b, E', E", G} z relacijo <, ki je dana z
- {ø<a, ø<b, a<E', a<E", b<E', b<E", E'<G, E"<G}
kjer sta E' in E" dva roba in je G največja stranska ploskev.
Zgledi višjih rangov[uredi | uredi kodo]
Kot je bilo omenjeno, je pojem abstraktnega politopa zelo splošen. Vključuje:
- apeirogone, to je neskončne politope ali teselacije
- razčlembe drugih mnogoterosti kot sta torus ali realna projektivna ravnina
- mnogo drugih objektov kot sta 11-celica in 57-celica, ki običajno ne spadata v normalne geometrijske prostore.
V splošnem množica j stranskih ploskev tradicionalnega n-politopa tvori abstraktni n-politop.
Hozoedri in hozotopi[uredi | uredi kodo]

Dvokotnik je posplošitev hozoedra in več razsežnih hozotopov, ki jih realiziramo kot sferne poliedre. Vsi teselirajo sfero.
Projektivni politopi[uredi | uredi kodo]
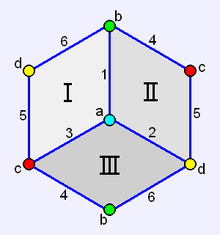
Zgledi neobičajnih abstraktnih poliedrov so polkocka (glej sliko), poloktaeder, poldodekaeder in polikozaeder. To so dvojniki platonskih teles. Lahko se jih realizira kot projektivne poliedre. Vsi teselirajo realno projektivno ravnino.
Polkocka je zgled tega kako se zapis s sliko oglišča ne more uporabiti za definicijo politopa. Vse 2-stranske ploskve in 3-stranske ploskve imajo isto skupino oglišč.
Dualnost[uredi | uredi kodo]
Vsak politop ima tudi svoj dual. Hassejev diagram duala je tisti, ki ima prvotni diagram obrnjen tako, da je zgornji del spodaj. V n-politopu se vsaka prvotna k-stranska ploskev preslika v (n-k-1)-stransko ploskev duala. To pomeni, da se n-stranska ploskev preslika v (-1)-stransko ploskev. Dual duala je izomorfen izvirniku.
Politop sebidualnemu politopu je isti politop. To pomeni, da je izomorfen svojemu dualu. Torej je Hassejev diagram sebidualnemu politopu simetričen okrog vodoravne osi na polovici med vrhom in dnom. Zgled: kvadratna piramida je sebidualna.
Incidenčne matrike[uredi | uredi kodo]
Politop se lahko prikaže z njegovimi incidencami. Spodnja incidenčna matrika je za trikotnik:
Matrika prikazuje točko povsod tam, kjer je stranska ploskev tudi podstranska. Zaradi tega je matrika simetrična okrog glavne diagonale. Prav tako daje odvečni podatek. Dovolj bi bilo, če bi prikazovala točke tam, kjer je vrstica za stransko ploskev ≤ vrstica za stolpec stranske ploskve.
| ø | a | b | c | ab | bc | ca | abc | |
|---|---|---|---|---|---|---|---|---|
| ø | • | • | • | • | • | • | • | • |
| a | • | • | • | • | • | |||
| b | • | • | • | • | • | |||
| c | • | • | • | • | • | |||
| ab | • | • | • | • | • | |||
| bc | • | • | • | • | • | |||
| ca | • | • | • | • | • | |||
| abc | • | • | • | • | • | • | • | • |
Glej tudi[uredi | uredi kodo]
Sklici[uredi | uredi kodo]
- ↑ McMullen ; Schulte (2002), str. 31.
Zunanje povezave[uredi | uredi kodo]
- Uvod v abstraktne politope Arhivirano 2011-07-08 na Wayback Machine. (angleško)
- Politopi abstraktni in realni (angleško)


