Torus

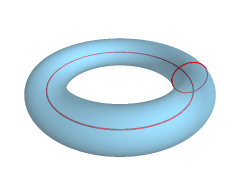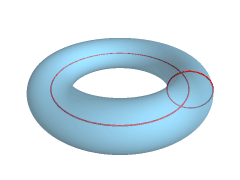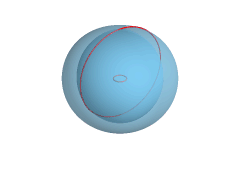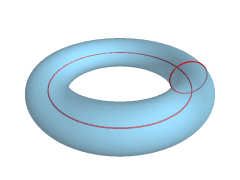
Tórus (ali svítek) je rotacijska ploskev, ki nastane z vrtenjem krožnice okrog osi, ki je koplanarna s krožnico. V večini primerov predpostavljamo, da se os ne dotika krožnice. Telo, ki pri tem nastane, se imenuje tóroid.
Rod torusa je enak 1.

Geometrija[uredi | uredi kodo]
Torus lahko definiramo v parametrični obliki [1]
kjer je

Razdalji in imenujemo tudi "veliki polmer" in "mali polmer".
Implicitna oblika enačbe torusa v kartezičnem koordinatnem sistemu za torus, ki je radialno simetričen na z-os je
ali v drugačni obliki, če je :
- .
Če odstranimo kvadratni koren, dobimo enačbo četrte stopnje
- .
Površina in prostornina torusa[uredi | uredi kodo]
Površina torusa je enaka
Prostornina pa je
- .
Topologija[uredi | uredi kodo]
Topološko je torus zaprta ploskev, ki je zmnožek dveh krožnic S1 × S1. Takšen topološki torus se imenuje tudi Cliffordov torus.
n-kratni torusi[uredi | uredi kodo]
 dvojni torus |
 trojni torus |
V teoriji ploskev ima izraz n-torus drugačen pomen. Namesto, da bi to pomenilo zmnožek n krožnic, to pomeni povezano vsoto n dvorazsežnih torusov.
Običajni torus je na ta način 1-torus, 2-torus imenujemo dvojni torus, 3-torus je trojni torus in tako dalje. Vedno pa lahko rečemo, da je n-torus orientabilna ploskev
Toroidni poliedri[uredi | uredi kodo]
Poliedri s topološkim tipom torusa se imenujejo toroidni poliedri.
Večrazsežni torusi[uredi | uredi kodo]
Torus lahko posplošimo na večje število razsežnosti. Na ta način dobimo n-razsežne toruse. Običajni torus je zmnožek prostorov dveh krožnic. N-razsežni torus (imenujemo ga tudi n-torus) pa je zmnožek krožnic, kar lahko zapišemo kot
- .
Torus, ki smo ga opisali zgoraj, je dvorazsežni torus, enorazsežni torus je kar krožnica.
Glej tudi[uredi | uredi kodo]
Opombe in sklici[uredi | uredi kodo]
- ↑ http://www.geom.uiuc.edu/zoo/toptype/torus/standard/eqns.html Arhivirano 2019-05-20 na Wayback Machine. Enačbe običajnega torusa
Zunanje povezave[uredi | uredi kodo]
- Torus na MathWorld (angleško)
- Prostornina torusa (angleško)
- Nekatere lastnosti torusa (angleško)


















