Conwayjeva notacija poliedrov

Conwayjeva notacija poliedrov se uporablja za opis poliedrov na osnovi osnovnega poliedra, ki ga spremenimo z različnimi operacijami.
Osnovni poliedri so platonska telesa, ki jih prikažemo s prvo črko njihovega imena (T, O, C, I, D) prizme (Pn) antiprizme (An) ali piramide (Yn). Vsak konveksni polieder lahko služi kot osnova, dokler lahko na njem izvajamo operacije.
Angleški matematik John Horton Conway (rojen 1937) je razširil zamisel o uporabi operatorjev kot je prisekanje, da bi izdelal sorodne poliedre z isto simetrijo. Njegovi operatorji lahko generirajo vsa arhimedska telesa in Catalanova telesa iz pravilnih osnovnih teles. Uporabljeni v skupini ti operatorji omogočajo nastanek mnogih poliedrov višjega reda.
Operacije nad poliedri[uredi | uredi kodo]
| operator | ime | alternativna konstrukcija |
oglišča | robovi | stranske ploskve | opis |
|---|---|---|---|---|---|---|
| osnovno telo | v | e | f | oblika osnove | ||
| r | reflekt (Hart) |
v | e | f | zrcalna slika kiralnih oblik | |
| d | dual | f | e | v | dualno telo osnovnega poliedra – vsako oglišče kreira novo stransko ploskev | |
| a | ambo | e | 2e | 2+e | robovi so nova oglišča, stara oglišča izginejo. (rektificirano) | |
| j | združen | da | e+2 | 2e | e | zametek je povečan s piramidami v dovolj veliki višini, tako, da imata 2 koplanarna trikotnika iz dveh različnih piramid skupen rob. |
| t | prisekan | dkd | 2e | 3e | e+2 | prisekana vsa oglišča. |
| -- | -- | dk | 2e | 3e | e+2 | dual oblike kis, (dvojna prisekanost) |
| -- | -- | kd | e+2 | 3e | 2e | kis oblika duala |
| k | kis | dtd | e+2 | 3e | 2e | dvigne piramido na vsaki stranski ploskvi. |
| c | ožlebljen | e+v | 4e | 2e+f | nove šestkotne stranske ploskve se dodajo namesto robov. | |
| - | - | dc | 2e+f | 4e | e+v | |
| e | razširjen | aa | 2e | 4e | 2e+2 | vsako oglišče ustvari novo stransko ploskev in vsak rob ustvari nov štirikotnik. (kantelirano) |
| o | orto | de | 2e+2 | 4e | 2e | vsaka n-kotnikova stranska ploskev se razdeli v n štirikotnike. |
| p | propeler (Hart) |
v+2e | 4e | e+f | vrtenje stranskih ploskev, ki ustvari štirikotnike na ogliščih (sebi-dualne) | |
| - | - | dp | e+f | 4e | v+2e | |
| s | prirezanost | dg | 2e | 5e | 3e+2 | "razširi in zvij" – vsako oglišče ustvari novo stransko ploskev in vsak rob ustvari dva nova trikotnika |
| g | giro | ds | 3e+2 | 5e | 2e | vsaka n-kotnikova stranska ploskev se deli na n petkotnikov. |
| b | nagnjen | ta | 4e | 6e | 2e+2 | nove stranske ploskve se dodajo na mesta robov in oglišč omniprisekanost (znana tudi kot kantiprisekanost v višjih politopih). |
| m | meta | db & kj | 2e+2 | 6e | 4e | n-kotne stranske ploskve se razdelijo v 2n trikotnikov |
Posebne oblike postopek kis ima variacijo kn, ki doda piramide na stranske ploskve, ki imajo n stranic operator prisekanosti ima variante tn, ki samo prisekajo oglišča z redom n.
Operatorji se izvajajo od desne proti levi. Zgled: * dual tetraedra je dT
- prisekanje kocke je t3C ali tC
- prisekanje kubooktaedra je T4aC ali taC.
Vse operacije ohranjajo simetrijo, razen zvijanja.
Zgledi[uredi | uredi kodo]
Kocka lahko generira vse konveksne uniformne poliedre z oktaedrsko simetrijo.
| kocka "osnova" (zametek) |
ambo (rektificirano) |
prisekano | dvojno prisekano | razširjeno (kantelirano) |
nagnjeno (omniprisekano) |
prirezanost |
|---|---|---|---|---|---|---|
 C |
 aC = djC |
 tC = dkdC |
 tdC = dkC |
 eC = aaC = doC |
 bC = taC = dmC = dkjC |
 sC = dgC |
| dualni | združen | kis (razpolovljeno oglišče) |
orto (razpolovljen rob) |
meta (polno razpolovljeno) |
giro | |
 dC |
 jC = daC |
 kdC = dtC |
 kC = dtdC |
 oC = deC = daaC |
 mC = dbC = kjC |
 gC = dsC |
Generiranje pravilnih osnovnih teles[uredi | uredi kodo]
Vseh pet pravilnih poliedrov se lahko generira iz prizmatičnih generatorjev z nič ali eno operacijo.
- trikotna piramida: Y3 (tetraeder je posebna piramida)
- T = Y3
- O = aY3 (rektificirani tetraeder)
- C = daY3 (dual rektificiranega tetraedra)
- I = sY3 (prirezani tetraeder)
- D = dsY3 (dual prirezanega tetraedra)
- trikotna antiprizma: A3 (oktaeder je posebna antiprizma)
- O = A3
- C = dA3
- kvadratna prizma: P4 (kocka je posebna prizma)
- C = P4
- petstrana antiprizma: A5
- I = k5A5 (posebna giropodaljšana dipiramida)
- D = t5dA5 (posebni prisekani trapezoeder)
Razširitev Conwayjevih simbolov[uredi | uredi kodo]
Zgornje operacije omogočajo, da se polpravilni poliedri in Catalanova telesa generirajo iz pravilnih poliedrov. S kombinacijo operacij lahko dobimo še več višjih operacij. Veliko zanimivih poliedrov višjega reda zahteva sestavo novih operatorjev.
Geometrijski umetnik George William Hart (rojen 1955) je kreiral operacijo, ki jo je imenoval propeler ter še eno operacijo z imenom reflekt s katero je kreiral zrcalne slike vrtečih se oblik.
- "propeler" pomeni operacijo vrtenja, ki kreira štirikotnike na ogliščih. Ta operacija je sebi dualna: dpX = pdX.
- "reflekt" kreira zrcalno sliko osnovnega telesa. Nima pravega efekta razen, če je osnovno telo narejeno z s ali g.
Geometrijske koordinate izpeljanih oblik[uredi | uredi kodo]
 D |
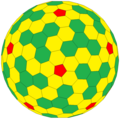
 tD |
 aD |
 tdD |
 eD |
 teD |
 sD |
 dD |
 dteD |
 H |
 tH |
 aH |
 tdH = H |
 eH |
 teH |
 sH |
 dH |
 dtH |
 daH |
 dtdH = dH |
 deH |
 dteH |
 dsH |
 T |
 tT |
 T |
 tdT |
 eT |
 bT |
 sT |
 dT |
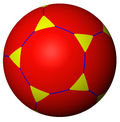
 dtT |
 jT |
 kT |
 oT |
 mT |
 gT |
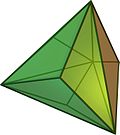
| {7,3} "osnova" |
prisekano | ambo (rektificirano) |
dvojno prisekano | razširjeno (kantelirano) |
bevel (omniprisekano) |
prirezana oblika |
|---|---|---|---|---|---|---|

|
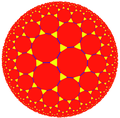
|

|
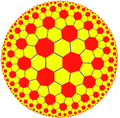
|

|

|
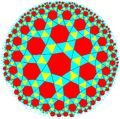
|
| dual | združeno | kis (razpolovitev oglišča) |
orto (razpolovitev roba) |
meta (polna razpolovitev) |
giro | |

|

|

|

|

|

|

|
Ostali poliedri[uredi | uredi kodo]
Tetraedrska simetrija[uredi | uredi kodo]
Oktaedrska simetrija[uredi | uredi kodo]
-
prisekani rombski dodekaeder
"t4daC" -
tetrakisni kubooktaeder
"k4aC" -
"dk4sC"
Ikozaedrska simetrija[uredi | uredi kodo]
Rombska:
-
rombski eneakontaeder
"dakD"
Trikotni:
-
"k6k5tI"
-
"kt5daD"
-
"kdktI"
"dtktI" -
"kdkt5daD"
Dualni trikotni:
-
prisekani ikozaeder
"dkD" -
"dk6k5tI"
-
"dkt5daD"
-
"tktI"
-
"tkt5daD"
Trikotni kiralni:
-
"k5k6stI"
"kdk5sD"
Dualni trikotni kiralni:
-
"sD"
-
"dk5sD"
-
"dk5k6stI"
"tk5sD"
Glej tudi[uredi | uredi kodo]
Zunanje povezave[uredi | uredi kodo]
- Conwayjeva notacija za poliedre (angleško)
- Imena poliedrov (angleško)
- Weisstein, Eric Wolfgang. »Conway Polyhedron Notation«. MathWorld.
- Conwayjeva notacija (angleško)
- Weisstein, Eric Wolfgang. »Truncation«. MathWorld.
- Weisstein, Eric Wolfgang. »Rectification«. MathWorld.
- Weisstein, Eric Wolfgang. »Cumulation«. MathWorld.
- Conwayjevi operatorji (angleško)
- Izpeljana telesa (angleško)