Uniformni polieder

Uniformni polieder je polieder, ki ima za stranske ploskve pravilne mnogokotnike, ki so tranzitivni na svojih ogliščih (to pomeni, da obstoja togi premik (izometrija) za preslikavo poljubnega oglišča v drugega). To pomeni tudi, da so vsa oglišča skladna. Poliedri imajo visoko stopnjo zrcalne in rotacijske simetrije.

Uniformni poliedri so lahko

• pravilni, če so stranske ploskve in robovi tranzitivni
• kvazipravilni, če so robovi tranzitivni, niso pa tranzitivne stranske ploskve
• polpravilni pa so, če robovi niso tranzitivni, niti stranske ploskve niso tranzitivne.

Poznamo konveksne

• 5 platonskih teles, ki so pravilni poliedri
• 13 arhimedovih teles od kateri sta 2 kvazipravilni in 11 polpravilnih

in zvezdne poliedre od katerih so

• 4 Kepler-Poinsotov polieder, ki so pravilni nekonveksni poliedri
• 53 uniformni zvezdni polieder od katerih je 5 kvazipravilnih in 48 polpravilnih
• 1 zvezdni polieder, ki ga je našel ameriški gradbenik in arhitekt John Skilling (1921 – 1998).

Znanih je tudi neskončno število uniformnih prizmatičnih in antiprizmatičnih oblik med katerimi so konveksne in zvezdne oblike.

Dualni poliedri uniformnih poliedrov imajo tranzitivne stranske ploskve ali lahko rečemo tudi, da so izoederski. Imajo tudi pravilne slike oglišč ter jih tako razvrstimo skupaj z dualnimi uniformnimi poliedri. Dualno telo pravilnega poliedra je tudi pravilen. Dualna telesa arhimedskih teles pa pravimo, da so Catalanova telesa.

Razvoj

Platonska telesa so poznali že v Antični Grčiji. Proučevali so jih že Platon (427 pr. n. št-437 pr. n. št., Teetet (417 pr. n. št.-369 pr. n. št.) in Evklid (okoli 365 pr. n. št.-275 pr. n. št.).

• Johannes Kepler (1571-1630) je bil prvi, ki je objavil popoln seznam arhimedskih teles kmalu za tem, ko je bilo prvotno delo Arhimeda izgubljeno.

Pravilni zvezdni poliedri:

• Kepler je odkril še dva pravilna Kepler-Poinsotova poliedra.

Pozneje (v letu 1809) je Louis Poinsot (1777-1859) odkril še dva.

Ostalih 53 nepravilnih zvezdnih poliedrov

• Od ostalih 53 jih je v letu 1881 Albert Badoureau odkril še 36, Edmund Hess (1843-1903) je odkril še dva in Pitch (1930-1932) jih je neodvisno v letu 1881 odkril še 18, vendar odkritja ni objavil, od teh jih je bilo 15 že prej odkritih.
• Geometer H.S.M. Coxeter (1907-2003) je odkril še preostalih dvanajst v sodelovanju z J. C. P. Millerjem (1930-1932), kar pa ni bilo objavljeno. M. S. in H. C. Lonquet-Higgins sta jih neodvisno odkrila še 11.
• Coxeter, Lonquet-Higgins in Miller so v letu 1954 objavili seznam uniformnih poliedrov
• Sopov je dokazal. Da je njihov seznam popoln.
• Leta 1970 je v knjigi Polyhedron models (Modeli poliedrov), ki prikazuje vseh 75 neprizmatičnih uniformnih poliedrov, od katerih jih mnogo prej še ni bilo objavljenih. Imena pa jim je dal Norman Johnson (rojen 1930).
• Skilling (1921-1998) je v letu 1975 preveril to trditev in pokazal, da takrat, ko sprostimo definicijo toliko, da omogočimo tudi hkratnost robov in s tem dobimo še eno možnost za telo.
• V letu 1993 je Zvi Har'El pripravil popolno kalejdoskopsko konstrukcijo za uniformne poliedre in njihove duale s pomočjo računalniškega programa, ki se je imenoval Kaleido. Vse je združil v dokumentu Uniform Solution for Uniform Polyhedra, kjer je oštevilčil oblike s številkami od 1 do 80.
• Prav tako je v letu 1993 R.Mäder prenesel to Kaleido rešitev v program Mathematica z drugačnim načinom številčenja.
• V letu 2002 je Peter W. Messer odkril najmanjšo množico zaprtih oblik izrazov, ki določajo glavne in metrične količine za vsak uniformni polieder, dane s samo Wythoffovim simbolom .

Uniformni zvezdni poliedri

57 neprizmatičnih nekonveksnih oblik dobimo s pomočjo Wythoffove konstrukcije in s pomočjo Schwarzovih trikotnikov

Konveksne oblike po Wythoffovi konstrukciji

Konveksne uniformne poliedre lahko imenujemo po operacijah Wythoffove konstrukcije.

Podrobnejši načini Wythoffove konstrukcije so podani spodaj za vsako simetrijsko grupo posebej.

Z Wythoffovo konstrukcijo se dobijo ponovitve, ki nastanejo zaradi oblike z najnižjo simetrijo. Kocka in kvadratna prizma sta pravilna poliedra. Oktaeder in tristrana antiprizma sta tudi pravilna poliedra. Oktaeder je rektificiran tetraeder. Mnogi poliedri so ponovitve začetnih različnih konstrukcij in jih različno obarvamo.

Wythoffova konstrukcija se lahko uporabi za uniformne poliedre in uniformno tlakovanje na sferi. Zaradi tega so prikazane slike obeh možnosti. Sferno tlakovanje vključuje hozoedre in diedre, ki pa so degenerirani poliedri.

Te simetrijske grupe nastajajo iz zrcalnih točkovnih grup v treh razsežnostih. Vsako lahko prikažemo z osnovnim trikotnikom (p q r), kjer je p>1, q>1, r>1 in 1/p+1/q+1/r<1.

• tetraederska simetrija (3 3 2) red 24
• oktaederska simetrija (4 3 2) red 48
• ikozaederska simetrija (5 3 2) red 120
• diederska simetrija (n 2 2) za vse n = 3,4,5.... red 4n

Ostale nezrcalne oblike se lahko konstruira s pomočjo operacije alternacije, ki jo uporabimo za poliedre s parnim številom stranic.

Razen vseh prizem z diedersko simetrijo nam lahko postopek Wythoffove konstrukcije doda še dva pravilna razreda, ki pa postaneta izrojena kot poliedra. To sta dieder in hozoeder. Prvi ima samo dve stranski ploskvi, drugo pa samo dve oglišči. Prisekanje hozoedra nam da prizmo.

V spodnjem pregledu imajo uniformni poliedri oznake (indekse) od 1 do 18 za neprizmatične oblike, ker so predstavljeni v pregledih s simetrijsko obliko. Ponovljene oblike so v oklepajih.

Neskončna množica prizmatičnih oblik je označena s štirimi družinami:

1. hozoedri H_2... samo kot sferno tlakovanje
2. diedri D_2... samo kot sferno tlakovanje
3. prizme P_2...
4. antiprizme A_3...

Skupna preglednica

Johnsonovo ime	Starševsko telo	Prisekano	Rektificirano	Biprisekano	Birektificirano	Kantelirano	Omniprisekano (kantiprisekano )	Prirezano
Razširjen Schläflijev simbol	$\begin{Bmatrix} p , q \end{Bmatrix}$	$t\begin{Bmatrix} p , q \end{Bmatrix}$	$\begin{Bmatrix} p \\ q \end{Bmatrix}$	$t\begin{Bmatrix} q , p \end{Bmatrix}$	$\begin{Bmatrix} q , p \end{Bmatrix}$	$r\begin{Bmatrix} p \\ q \end{Bmatrix}$	$t\begin{Bmatrix} p \\ q \end{Bmatrix}$	$s\begin{Bmatrix} p \\ q \end{Bmatrix}$
	t0{p,q}	t0,1{p,q}	t1{p,q}	t1,2{p,q}	t2{p,q}	t0,2{p,q}	t0,1,2{p,q}	s{p,q}
Wythoffov simbol p-q-2	q | p 2	2 q | p	2 | p q	2 p | q	p | q 2	p q | 2	p q 2 |	| p q 2
Coxeter-Dynkinov diagram
Slika oglišča	pq	(q.2p.2p)	(p.q.p.q)	(p. 2q.2q)	qp	(p. 4.q.4)	(4.2p.2q)	(3.3.p. 3.q)
tetraederska 3-3-2	{3,3}	(3.6.6)	(3.3.3.3)	(3.6.6)	{3,3}	(3.4.3.4)	(4.6.6)	(3.3.3.3.3)
oktaederska 4-3-2	{4,3}	(3.8.8)	(3.4.3.4)	(4.6.6)	{3,4}	(3.4.4.4)	(4.6.8)	(3.3.3.3.4)
ikozaederska 5-3-2	{5,3}	(3.10.10)	(3.5.3.5)	(5.6.6)	{3,5}	(3.4.5.4)	(4.6.10)	(3.3.3.3.5)

in primeri diederskih simetrij:

(p 2 2)	Starševsko telo	Prisekano	Rektificirano	Biprisekano	Birektificirano	Kantelirano	Omniprisekano (kantiprisekano)	Prirezano
Razširjen Schläflijev simbol	$\begin{Bmatrix} p , 2 \end{Bmatrix}$	$t\begin{Bmatrix} p , 2 \end{Bmatrix}$	$\begin{Bmatrix} p \\ 2 \end{Bmatrix}$	$t\begin{Bmatrix} 2 , p \end{Bmatrix}$	$\begin{Bmatrix} 2 , p \end{Bmatrix}$	$r\begin{Bmatrix} p \\ 2 \end{Bmatrix}$	$t\begin{Bmatrix} p \\ 2 \end{Bmatrix}$	$s\begin{Bmatrix} p \\ 2 \end{Bmatrix}$
	t0{p,2}	t0,1{p,2}	t1{p,2}	t1,2{p,2}	t2{p,2}	t0,2{p,2}	t0,1,2{p,2}	s{p,2}
Wythoffov simbol	2 | p 2	2 2 | p	2 | p 2	2 p | 2	p | 2 2	p 2 | 2	p 2 2 |	| p 2 2
Coxeter-Dynkinov diagram
Slika oglišča	p2	(2.2p.2p)	(p. 2.p. 2)	(p. 4.4)	2p	(p. 4.2.4)	(4.2p.4)	(3.3.p. 3.2)
diederska (2 2 2)	{2,2}	2.4.4	2.2.2.2	4.4.2	{2,2}	2.4.2.4	4.4.4	3.3.3.2
diederska (3 2 2)	{3,2}	2.6.6	2.3.2.3	4.4.3	{2,3}	2.4.3.4	4.4.6	3.3.3.3
diederska (4 2 2)	{4,2}	2.8.8	2.4.2.4	4.4.4	{2,4}	2.4.4.4	4.4.8	3.3.3.4
diederska (5 2 2)	{5,2}	2.10.10	2.5.2.5	4.4.5	{2,5}	2.4.5.4	4.4.10	3.3.3.5
diederska (6 2 2)	{6,2}	2.12.12	2.6.2.6	4.4.6	{2,6}	2.4.6.4	4.4.12	3.3.3.6

Operatorji za Wythoffovo konstrukcijo

Zgledi za oblike od kocke do oktaedra

Operacija	Razširjeni Schläflijevi simboli		Coxeter- Dynkinov diagram	Opis
Starševsko telo	t0{p,q}	$\begin{Bmatrix} p , q \end{Bmatrix}$		za poljubni pravilni polieder ali tlakovanje
Rektifikacija	t1{p,q}	$\begin{Bmatrix} p \\ q \end{Bmatrix}$		Robovi so popolnima prirezani v točke. Poliedri imajo kombinirane stranske ploskve svojega starševskega telesa in njegovega duala.
Birektifikacija tudi dual	t2{p,q}	$\begin{Bmatrix} q , p \end{Bmatrix}$		Birektificiranost (tudi za dual) je nadaljevanje prisekanja tako, da so prvotne stranske ploskve zmanjšane do točk. Nove stranske ploskve nastanejo pod vsakim starševskim ogliščem. Število robov ostane nespremenjeno in se zavrti za 90º. Dualno telo pravilnega poliedra {p, q} je tudi pravilni polieder {q, p}.
Prisekanost	t0,1{p,q}	$t\begin{Bmatrix} p , q \end{Bmatrix}$		Vsako prvotno oglišče je odrezano, z nastankom nove stranske ploskve se izpopolni praznina. Prisekanje ima prostostno stopnjo, ki ima rešitev za kreiranje uniformnega prisekanega poliedra. Polieder ima svoje prvotne stranske ploskve podvojene ter vsebuje stranske ploskve duala.
Biprisekanost	t1,2{p,q}	$t\begin{Bmatrix} q , p \end{Bmatrix}$		isto kot prisekan dual.
Kanteliranost (ali rombiranost) (tudi razširjenost)	t0,2{p,q}	$r\begin{Bmatrix} p \\ q \end{Bmatrix}$		Razen prisekanja oglišč je vsak prvotni rob nagnjen zaradi novega pravokotne stranske ploskve, ki se pojavi namesto njega. Uniformna kantelacija je približno na polovici med starševsko in dualno obliko.
Omniprisekanost (ali kantiprisekanost)	t0,1,2{p,q}	$t\begin{Bmatrix} p \\ q \end{Bmatrix}$		Prisekanost in kantelacija sta uporabljeni skupaj, da bi ustvarili omniprisekano obliko, ki podvoji stranice stranskih ploskev starševskega telesa in podvoji stranice stranskih ploskev ter kvadratov, kjer so bili prvotni robovi.
Prirezanost	s{p,q}	$s\begin{Bmatrix} p \\ q \end{Bmatrix}$		Prirezane oblike zavzamejo omniprisekanost in pri tem rektificirajo vsako drugo oglišče. (ta operacije je možna samo, če ima polieder parno število stranskih ploskev) Vse prvotne stranske ploskve končajo tako, da dobimo samo polovico stranic, kvadrati pa se izrodijo v robove. Ker ima omniprisekana oblika 3 stranske ploskve/oglišče nastanejo novi trikotniki. Pogosto je to izmenično facetiranje popačeno, tako, da se konča kot uniformni poliedri. Možnost kasnejših sprememb je odvisna od stopnje prostosti.

(3 3 2) T_d tetraederska simetrija

Tetraederska simetrija sfere generira 5 uniformnih poliedrov in šesto obliko s pomočjo operacije prirezovanja.

Tetraedersko simetrijo lahko prikažemo s pomočjo osnovnega trikotnika z enim ogliščem s tremi zcali, ki jih prikažemo s simbolom (3 3 2). Lahko jih tudi prikažemo s Coxeterjevo grupo A₂ or [3,3] in seveda s Coxeter-Dynkinovim diagramom: .

Obstoja 24 trikotnikov, ki jih vidimo na stranskih ploskvah tetrakisnega heksaedra in izmenoma pobarvanih trikotnikih na sferi:

#	Ime	Graf A3	Graf A2	Slika	Tlakovanje	Oglišč slika	Coxeter-Dynkinov diagram in Schläflijevi simboli	Število stranskih ploskev po položaju			Število elementov
								položaj 2 [3] (4)	položaj 1 [2] (6)	položaj 0 [3] (4)	Stranske ploskve	Robovi	Oglišča
1	tetraeder (tet)						{3,3}	{3}			4	6	4
[1]	birektificiran tetraeder (tet) (isto kot tetraeder)						t2{3,3}			{3}	4	6	4
2	rektificiran tetraeder (oct) (isto kot oktaeder)						t1{3,3}	{3}		{3}	8	12	6
3	prisekan tetraeder (tut)						t0,1{3,3}	{6}		{3}	8	18	12
[3]	biprisekan tetraeder (tut) (isto kot prisekan tetraeder)						t1,2{3,3}	{3}		{6}	8	18	12
4	kanteliran tetraeder (co) (isto kot kubooktaeder)						t0,2{3,3}	{3}	{4}	{3}	14	24	12
5	omniprisekan tetraeder (toe) (isto kot prisekan oktaeder)						t0,1,2{3,3}	{6}	{4}	{6}	14	36	24
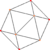
6	prirezan tetraeder (ike) (isto kot ikozaeder)						s{3,3}	{3}	2 {3}	{3}	20	30	12

(4 3 2) O_h oktaederska simetrija

Oktaederska simetrija sfere generira 7 uniformnih poliedrov in še tri z alternacijo. Štirje od teh oblik so ponovitve tetraederske simetrije iz preglednice zgoraj.

Oktaedersko simetrijo lahko prikažemo s pomočjo osnovnega trikotnika (4 3 2) tako, da upoštevamo zrcala na vsakem oglišču. Lahko jih prikažemo tudi kot Coxeterjevo grupo B₂ ali [4,3] in kot Coxeter-Dynkinov diagram: .

Obstoja 48 trokotnikv, ki jih vidimo na stranskih ploskvah disdiakisnega dodekaedra in izmenoma pobarvanih trikotnikov na sferi:

#	Ime	Graf B3	Graf B2	Slika	Tlakovanje	Slika oglišč	Coxeter-Dynkinov diagram in Schläflijevi simboli	Število stranskih ploskev po položaju			Število elementov
								položaj 2 [4] (8)	položaj 1 [2] (12)	položaj 0 [3] (6)	Stranske ploskve	Robovi	Oglišča
7	kocka (kocka)						{4,3}	{4}			6	12	8
[2]	oktaeder (oct)						{3,4}			{3}	8	12	6
[4]	rektificirana kocka (co) rektificiran oktaeder (kubooktaeder)						{4,3}	{4}		{3}	14	24	12
8	prisekana kocka (tic)						t0,1{4,3}	{8}		{3}	14	36	24
[5]	prisekan oktaeder (toe)						t0,1{3,4}	{4}		{6}	14	36	24
9	kantelirana kocka (sirco) kanteliran oktaeder rombikubooktaeder						t0,2{4,3}	{8}	{4}	{6}	26	48	24
10	omniprisekana kocka (girco) omniprisekan oktaeder prisekan kubooktaeder						t0,1,2{4,3}	{8}	{4}	{6}	26	72	48
[6]	alterniran prisekan oktaeder (ike) (isto kot ikozaeder)						h0,1{3,4}		{3}	{3}	20	30	12
[1]	alternirana kocka (tet) (isto kot tetraeder)						h{4,3}			1/2 {3}	4	6	4
11	prirezana kocka (snic)						s{4,3}	{4}	2 {3}	{3}	38	60	24

(5 3 2) I_h ikozaederska simetrija

Ikozaederska simetrija sfere generira 7 uniformnih poliedrov in še enega več z alternacijo. Samo eden se ponavlja v preglednici z tetraedersko in oktaedersko simetrijo v preglednici zgoraj.

Ikozaedersko simetrijo lahko prikažemo z osnovnim trikotnikom (5 3 2), pri tem pa štejemo zrcala na vsakem oglišču. Lahko ga prikažemo tudi s pomočjo Coxeterjeve grupe G₂ ali [5,3] s pomočjo Coxeter-Dynkinovega diagrama: .

Obstoja 120 trikotnikov, ki jih vidimo na stranskih ploskvah disdiakisni triakontaeder in na izmenoma pobarvanih trikotnikih na sferi:

#	Ime	Graf (A2) [6]	Graf (H3) [10]	Slika	tlakovanje	slika oglišč	Coxeter-Dynkinov diagram in Schläflijevi simboli	Število stranskih ploskev po položaju			Število elementov
								položaj 2 [5] (12)	položaj 1 [2] (30)	položaj 0 [3] (20)	Stranske ploskve	Robovi	Oglišča
12	dodekaeder (doe)						{5,3}	{5}			12	30	20
[6]	ikozaeder (ike)						{3,5}			{3}	20	30	12
13	rektificirani dodekaeder (id) rektificirani ikozaeder ikozidodekaeder						t1{5,3}	{5}		{3}	32	60	30
14	prisekan dodekaeder (tid)						t0,1{5,3}	{10}		{3}	32	90	60
15	prisekan ikozaeder (ti)		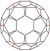				t0,1{3,5}	{5}		{6}	32	90	60
16	kantelirani dodekaeder (srid) kanteliran ikozaeder rombiikozidodekaeder						t0,2{5,3}	{5}	{4}	{3}	62	120	60
17	Omniprisekan dodekaeder (grid) Omniprisekan ikozaeder prisekan ikozidodekaeder						t0,1,2{5,3}	{10}	{4}	{6}	62	180	120
18	prirezan dodekaeder (snid) prirezan ikozaeder						s{5,3}	{5}	2 {3}	{3}	92	150	60

(p 2 2) Prizmatična družina [p,2], I₂(p) (D_ph diederska simetrija)

Diederska simetrija sfere generira dve neskončni množici uniformnih poliedrov, prizem in antiprizem, prav tako pa tudi neskončno množico izrojenih mnogokotnikov, hozoedrov in diedrov, ki obstojajo kot tlakovanja sfere. Diederska simetrija se lahko prikaže kot onovni trikotnik (p 2 2) s tem, da upoštevamo zrcala na vsakem oglišču. Lahko se prikaže tudi kot Coxeterjeva grupa I₂(p) or [n,2], in tudi kot prizmatični Coxeter-Dynkinov diagram: .

Spodaj je prvih pet diederskih simetrij: D₂ ... D₆. Diederska simetrija D_p ima red 4n, ki se kaže na stranskih ploskvah bipiramide in na sferi kot ekvatorska črta na longitudi in n enakomerno razmaknjenih črt longitude.

(2 2 2) diederska simetrija

Obstoja 8 osnovnih trikotnikov, ki se vidijo na stranskih ploskvah kvadratne bipiramide (oktaeder), ki ima imenoma obarvane trikotnike na sferi:

#	Ime	Slika	Tlakovanje	Slika oglišč	Coxeter-Dynkinov diagram in Schläflijevi simboli	Število stranskih ploskev po položaju			Število elementov
						položaj 2 [2] (2)	položaj 1 [2] (2)	položaj 0 [2] (2)	Stranske ploskve	Robovi	Oglišča
D2 H2	digonalni dieder digonalni hozoeder				{2,2}	{2}			2	2	2
D4	prisekan digonalni dieder (isto kot kvadratni dieder)				t{2,2}={4,2}	{4}			2	4	4
P4 [7]	omniprisekan digonalni dieder (kocka) (isto kot kocka)				t0,1,2{2,2}	{4}	{4}	{4}	6	12	8
A2 [1]	prirezan digonalni dieder (tet) (isto kot tetraeder)				s{2,2}		2 {3}		4	6	4

(3 2 2) D_3hdiederska simetrija

Obstoja 12 osnovnih trikotnikov, ki se vidijo na stranskih ploskvah šeststrane bipiramide ter izmenoma pobarvanih trikotnikih na sferi:

#	Ime	Slika	Tlakovanje	Slika oglišč	Coxeter-Dynkinov diagram in Schläflijevi simboli	Število stranskih ploskev po položaju			Število elementov
						položaj 2 [3] (2)	položaj 1 [2] (3)	položaj 0 [2] (3)	Stranske ploskve	Robovi	Oglišča
D3	trigonalni dieder				{3,2}	{3}			2	3	3
H3	trigonalni hozoeder				{2,3}			{2}	3	3	2
D6	prisekan trigonalni dieder (isto kot heksagonalni dieder)				t{3,2}	{6}			2	6	6
P3	prisekan trigonalni hozoeder (trip) (tristrana prizma)				t{2,3}	{3}	{4}		5	9	6
P6	omniprisekan trigonalni dieder (hip) (šeststrana prizma)				t{2,3}	{6}	{4}	{4}	8	18	12
A3 [2]	prirezan trigonalni dieder (oct) (isto kot tristrana antiprizma) (isto kot oktaeder)				s{2,3}	{3}	2 {3}		8	12	6

(4 2 2) D_4hdiederska simetrija

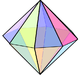Obstoja 16 osnovnih trikotnikov, ki se vidijo na stranskih ploskvah osemstrane bipiramide ter izmenoma pobarvani trikotniki na sferi:

#	Ime	Slika	Tlakovanje	Slika oglišč	Coxeter-Dynkinov diagram in Schläflijevi simboli	Število stranskih ploskev po položajih			Število elementov
						položaj 2 [4] (2)	položaj 1 [2] (4)	položaj 0 [2] (4)	Stranske ploskve	Robovi	Oglišča
D4	kvadratni dieder				{4,2}	{4}			2	4	4
H4	kvadratni hozoeder				{2,4}			{2}	4	4	2
D8	prisekan kvadratni dieder (isto kot oktagonalni dieder)				t{4,2}	{8}			2	8	8
P4 [7]	prisekan kvadratni hozoeder (kocka) (kocka)				t{2,4}	{4}	{4}		6	12	8
D8	Omniprisekan kvadratni dieder (op) (osemstrana prizma)				t{2,4}	{8}	{4}	{4}	10	24	16
A4	prirezan kvadratni diedr (squap) (kvadratna antiprizma)				t{2,4}	{4}	2 {3}		10	16	8

(5 2 2) D_5h diederska simetrija

Obstoja 20 osnovnih trikotnikov, ki so vidni na stranskih ploskvah desetstrane bipiramide ter izmenoma obarvani trikotniki na sferi:

#	Ime	Slika	Tlakovanje	Slika oglišč	Coxeter-Dynkinov diagram in Schläflijevi simboli	Število stranskih plokev po položaju			Število elementov
						položaj 2 [5] (2)	položaj 1 [2] (5)	položaj 0 [2] (5)	Stranske ploskve	Robovo	Oglišča
D5	petstrani dieder				{5,2}	{5}			2	5	5
H5	petstrani hozoeder				{2,5}			{2}	5	5	2
D10	prisekan petstrani dieder (isto kot dvanajststrani dieder)				t{5,2}	{10}			2	10	10
P5	prisekan petstrani hozoeder (pip) (isto kot petstrana prizma)				t{2,5}	{5}	{4}		7	15	10
P10	Omniprisekan petkotni dieder (dip) (dekagonalna prizma)				t{2,5}	{10}	{4}	{4}	12	30	20
A5	prirezan petkotni dieder (pap) (petstrana antiprizma)				t{2,5}	{5}	2 {3}		12	20	10

(6 2 2) D_6hdiederska simetrija

Obstoja 24 osnovnih trikotnikov , ki se vidijo na stranskih ploskvah dvanajststrane bipiramide in na izmenoma pobarvanimi trikotniki na sferi.

#	Ime	Slika	Tlakovanje	Slika oglišč	Coxeter-Dynkinov diagram in Schläflijevi simboli	Število stranskih ploskev po položaju			Število elementov
						položaj 2 [6] (2)	položaj 1 [2] (6)	položaj 0 [2] (6)	Stranske ploskve	Robovi	Oglišča
D6	šeststrani dieder				{6,2}	{6}			2	6	6
H6	šeststrani hozoeder				{2,6}			{2}	6	6	2
D12	prisekan šeststrani dieder (isto kot dodekagonalni dieder)				t{6,2}	{12}			2	12	12
H6	prisekan šestkotni hozoeder (hip) (isto kot šeststrana prizma)				t{2,6}	{6}	{4}		8	18	12
P12	Omnipriseksn šeststrani dieder (twip) (dvanajststrana prizma)				t{2,6}	{12}	{4}	{4}	14	36	24
A6	prirezan šeststrani dieder (hap) (šeststrana antiprizma)				t{2,6}	{6}	2 {3}		14	24	12

Glej tudi

• polieder
  • pravilni polieder
  • kvazipravilni polieder
  • polpravilni polieder
• seznam uniformnih poliedrov
• seznam modelov Wenningerjevih poliedrov

Zunanje povezave

• Uniformni polieder na MathWorld (v angleščini)
• Nekonveksni uniformni poliedri v Encyclopedia of Science (v angleščini)
• Uniformni poliedri (v angleščini)
• Uniformni poliedri (v angleščini)