Dvanajstkotnik
Dvanajstkotnik (s tujko tudi dodekagon) je mnogokotnik z dvanajstimi stranicami, dvanajstimi oglišči in dvanajstimi notranjimi koti. Spada med pravilne mnogokotnike.
Pravilni dvanajstkotnik[uredi | uredi kodo]
Običajno pod izrazom dvanajstkotnik mislimo pravilni dvanajstkotnik. Ta ima enake stranice in kote, enake 150º. Njegov Schläflijev simbol je {12}. Coxeter-Dinkinov diagram je ![]()
![]()
![]() . Simetrijska grupa je diedrska.
. Simetrijska grupa je diedrska.
Ploščina pravilnega dvanajstkotnika z dolžino stranice a je:
Če je polmer očrtane krožnice enak R [1] je ploščina enaka:
Kadar je polmer včrtane krožnice enak r, je ploščina enaka:
Konstrukcija[uredi | uredi kodo]
Pravilni dvanajstkotnik lahko narišemo z ravnilom in šestilom. Spodaj je prikazan način risanja pravilnega dvanajstkotnika.

Uporaba[uredi | uredi kodo]
Prikazani so trije primeri periodičnega ravninskega tlakovanja z uporabo dvanajstkotnikov.
 Polpravilno tlakovanje 3.12.12 |
 Polpravilno tlakovanje: 4.6.12 |
 A demiregularno tlakovanje: 3.3.4.12 & 3.3.3.3.3.3 |
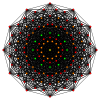
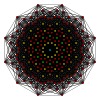
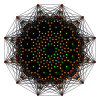
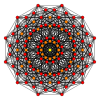
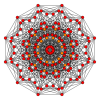
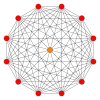
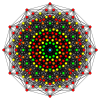
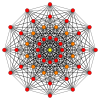
Petriejevi mnogokotniki[uredi | uredi kodo]
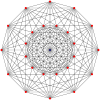
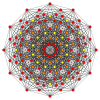
Pravilni dvanajstkotnik je Petriejev mnogokotnik za politope z višjo razsežnostjo, ki jih gledamo v ortogonalni projekciji v Coxeterjevih ravninah.
Opombe in sklici[uredi | uredi kodo]
- ↑ Glej tudi Kürschákove geometrijske preizkuse na the Wolfram Demonstration Project