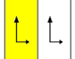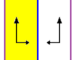Seznam grup ravninske simetrije
Seznam grup ravninske simetrije vsebuje razrede nezveznih ravninskih simetrijskih grup. Vsaka grupa je določena s tremi načini notacije. Te notacije so mednarodna notacija (tukaj označena kot IUC), notacija orbifold in Coxeterjeva notacija.
Uporabljajo se tri vrste grup simetrije v ravnini:
- 2 grupi rozete, ki sta dvorazsežni točkovni grupi
- 2 frizijski grupi, ki sta dvorazsežni grupi
- 17 tapetnih grup, ki so dvorazsežne prostorske grupe
Grupa rozete[uredi | uredi kodo]
Znani sta dve družini nezveznih dvorazsežnih točkovnih grup. Določena je s parametrom n, ki predstavlja red grup rotacij.
| družina | mednarodna notacija (notacija orbifold ) |
geo [1] |
Schönflies | Coxeter | red | primer |
|---|---|---|---|---|---|---|
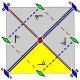
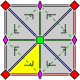
| ciklična simetrija | n (nn) |
n | Cn | [n]+ | n |  5-kratno vrtenje |
| diedrska simetrija | nm (*nn) |
n | Dn | [n] | 2n |  4-kratno zrcaljenje |
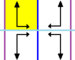
Frizijske grupe[uredi | uredi kodo]
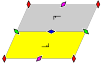
Sedem frizijskih grup, ki so dvorazsežne grupe na premici s smerjo, ki je dana s petimi imeni notacij. Schönfliesova notacija je dana z neskončno limito sedmih 7 diedrskih grup. Rumena področja predstavljajo neskončno osnovno domeno v vsaki. Enostavni primer je prikazan kot periodično tlakovanje na valju s periodičnostjo 6.
|
|
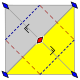
Tapetne grupe[uredi | uredi kodo]
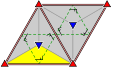
17 tapetnih grup s končnimi osnovnimi domenami je prikazanih z mednarodno notacijo, notacijo orbifold in Coxeterjevo notacijo, razvrščene v 5 Bravaisovih mrež v ravnini: kvadrato, poševnokotno (paralelogramsko), heksagonalno (60 stopinjsko rombsko), pravokotno in centrirano pravokotno (rombsko).
Grupe p1 in p2, ki nimajo zrcalne simetrije, se ponavljajo v vseh razredih. Podobna zrcalna Coxeterjeva grupa je podana v vseh razredih razen v nagnjenih.
|
|
|
Sklici[uredi | uredi kodo]
- ↑ The Crystallographic Space groups in Geometric algebra, D. Hestenes and J. Holt, Journal of Mathematical Physics. 48, 023514 (2007) (22 pages) PDF [1] Arhivirano 2020-10-20 na Wayback Machine.
Zunanje povezave[uredi | uredi kodo]
- Vodnik v orbifold notacijo (angleško)
- Tapetne grupe (angleško)
- Frizijske in ostale grupe (angleško)