Tlakovanje s pravilnimi mnogokotniki
Tlakovanje s pravilnimi mnogokotniki so uporabljali že v antiki.
Pravilna tlakovanja[uredi | uredi kodo]
Tlakovanje je pravilno, če je grupa simetrije tlakovanja deluje tranzitivno na zastave tlakovanja, kjer je zastava trojna in sestavljena iz medsebojno vstopajočih oglišč, robov in tlakovanja. To pomeni, da za vsak par zastav obstoja operacija simetrije, ki preslika prvo zastavo v drugo. To je enakovredno tlakovanju od roba do roba s skladnimi pravilnimi mnogokotniki. Obstojati mora šest enakostraničnih trikotnikov, štirje kvadrati ali trije pravilni šestkotniki v vsakem oglišču, ki dajo tri pravilne teselacije.
 36 trikotno tlakovanje |
 44 kvadratno tlakovanje |
 63 šestkotno tlakovanje |
Arhimedsko, uniformno in polpravilno tlakovanje[uredi | uredi kodo]
Ogliščna tranzitivnost pomeni, da za vsak par oglišč velja, da obstoja simetrijska operacija, ki preslika prvo oglišče v drugo.
Kombinacije pravilnih mnogokotnikov[uredi | uredi kodo]
Notranje kote mnogokotnikov, ki se srečajo v oglišču moramo dodati 360 stopinjam. Pravilni n-kotnik ima notranji kot enak stopinj. Obstoja 17 kombinacij pravilnih mnogokotnikov katerih notranje kote moramo dodati k 360 stopinjam. Vsak se obravnava kot vrsta oglišča. V štirih primerih nastopita dva različna ciklična reda mnogokotnikov. To nam da 21 vrst oglišč. Samo 11 se jih lahko pojavi v uniformnem tlakovanju pravilnih mnogokotnikov. Kadar se trije mnogokotniki srečajo v oglišču in ima eden med njimi neparno število stranic, morata imeti ostala dve isto velikost. Če je pa nimata bosta izmenoma nastopala okoli prvega mnogokotnika. To je pa nemogoče, če je število stranic neparno.
S tremi mnogokotniki v oglišču:
- 3.7.42 (ne more se pojaviti v nobenem tlakovanju pravilnih mnogokotnikov)
- 3.8.24 (ne more se pojaviti v nobenem tlakovanju pravilnih mnogokotnikov)
- 3.9.18 (ne more se pojaviti v nobenem tlakovanju pravilnih mnogokotnikov)
- 3.10.15 (ne more se pojaviti v nobenem tlakovanju pravilnih mnogokotnikov)
- 3.122 - pol-pravilno, prisekano šestkotno tlakovanje
- 4.5.20 (ne more se pojaviti v nobenem tlakovanju pravilnih mnogokotnikov)
- 4.6.12 - pol-pravilni, prisekano trišestkotno tlakovanje
- 4.82 - pol-pravilno, prisekano kvadratno tlakovanje
- 52.10 (ne more se pojaviti v nobenem tlakovanju pravilnih mnogokotnikov)
- 63 - pravilno, šestkotno tlakovanje
Spodaj so diagrami s takšnimi oglišči:
-
3.7.42
-
3.8.24
-
3.9.18
-
3.10.15
-
3.12.12
-
4.5.20
-
4.6.12
-
4.8.8
-
5.5.10
-
6.6.6
S štirimi mnogokotniki v oglišču:
- 32.4.12 - neuniformni, ima dve vrsti oglišč 32.4.12 in 36
- 3.4.3.12 - neuniformni imajo dve različni vrsti oglišč 3.4.3.12 in 3.3.4.3.4
- 32.62 - neuniformni se pojavljajo v dveh oblikah z oglišči 32.62/36 in 32.62/3.6.3.6.
- 3.6.3.6 - pol-pravilni, trišestkotno tlakovanje
- 44 - pravilni, kvadratno tlakovanje
- 3.42.6 - neuniformni, ima oglišča 3.42.6 in 3.6.3.6.
- 3.4.6.4 - pol-pravilni, rombitrišestkotno tlakovanje
Spodaj so diagrami s takšnimi oglišči:
-
3.3.4.12
-
3.4.3.12
-
3.3.6.6
-
3.6.3.6
-
4.4.4.4
-
3.4.4.6
-
3.4.6.4
S petimi mnogokotniki v oglišču:
- 34.6 - pol-pravilni, prirezano šestkotno tlakovanje se pojavlja v dveh enanciomorfnih oblikah. Slika oglišč dveh enanciomorfnih oblik je enaka. Rezultirajoča tlakovanja so različna.
- 33.42 - pol-pravilni, podaljšano trikotno tlakovanje
- 32.4.3.4 - pol-pravilno, prirezano kvadratno tlakovanje
Spodaj so diagrami s takšnimi oglišči:
-
3.3.3.3.6
-
3.3.3.4.4
-
3.3.4.3.4
S šestimi mnogokotniki v oglišču:
- 36 - pravilno, trikotno tlakovanje
Spodaj je diagram s takšnimi oglišči:
-
3.3.3.3.3.3
Ostala tlakovanja od roba do roba[uredi | uredi kodo]
Katerokoli število neuniformnih tlakovanj od roba do roba s pravilnimi mnogokotniki lahko narišemo. Prikazani so samo štirje primeri:
 32.62 in 36 |
 32.62 in 3.6.3.6 |
 32.4.12 in 36 |
 3.42.6 in 3.6.3.6 |
Hiperbolična ravnina[uredi | uredi kodo]
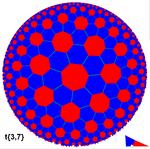
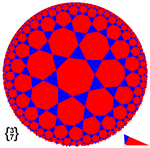
Te teselacije so povezane s pravilnimi in polpravilnimi poliedri in teselacijami v hiperbolični ravnini. Polpravilne poliedre sestavljajo stranske ploskve mnogokotnika toda njihovi koti prispevajo v vsaki točki k temu, da je kot 360 stopinj. Pravilni mnogokotniki v hiperbolični geometriji imajo kote, ki so manjši od kotov v ravnini. V obeh primerih je razporeditev mnogokotnikov enaka v vsakem oglišču.
V nadaljevanju je prikazanih nekaj pravilnih tlakovanj v hiperbolični ravnini z uporabo projekcije Poincaréjevega diskovnega modela.

|

|

|

|
|
|

|

|

|

|
Glej tudi[uredi | uredi kodo]
- seznam uniformnih tlakovanj
- Wythoffov simbol
- teselacija
- pravilni polieder
- polpravilni polieder
- hiperbolična geometrija
Zunanje povezave[uredi | uredi kodo]
- Uniformno tlakovanje Arhivirano 2006-09-09 na Wayback Machine. (angleško)
- Konstruiranje polpravilnih tlakovanj (angleško)
- Polpravilne teselacije na MathWorld (angleško)
- Polpravilne teselacije na MathWorld (angleško)
- Hiperbolično tlakovanje (angleško)
- Hiperbolične teselacije (angleško)