Tridesetkotnik

Pravilni tridesetkotnik

Tridesetkotnik (tudi 30-kotnik ali s tujko triakontagon) je mnogokotnik z 30-timi stranicami in 30-timi notranjimi koti.

Splošne značilnosti [uredi]

Ploščina (p) tridesetkotnika z dolžino stranice a je:

$p = \frac {15} {2}a^2 \cot \frac {\pi} {30} \!\, .$

Vsota vseh notranjih kotov dvajsetkotnika je enaka 5040º. Notranji kot je 168º, kar pomeni, da je zunanji kot enak 12º.

Simetrijska grupa je diederska D₃₀ oziroma t{15}. Notranji kot je približno 168º. Tridesetkotnik je konveksen, enakostraničen mnogokotnik, tetiven ter ima izogonalno in izotaksalno obliko. Njegova Coxeter-Dinkinova diagrama sta in .

Petrijevi mnogokotniki [uredi]

Pravilni tridesetkotnik je Petrijev mnogokotnik za mnoge večrazsežne politope s simetrijo E₈. Če jih prikažemo kot projicirane v poševni ortogonalni projekciji v Coxeterjevi ravnini E₈, imajo obliko:

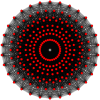(4₂₁)	t₁(4₂₁)	t₂(4₂₁)	(2₄₁)	t₁(2₄₁)

Tridesetkotnik je tudi Petrijev mnogokotnik za nekatere večrazsežne politope s simetrijo H₄, Če jih prikažemo v poševni ortogonalni projekciji v Coxeterjevi ravnini H₄, je to: