Funkcija

Za druge pomene glej Funkcija (razločitev).

Funkcija poveže vsakemu elementu v množici X (vhod oz. podatek) natančno en element v množici Y (izhod oz. rezultat). Dva različna elementa v X imata lahko isti izhod, in ni nujno, da so vsi elementi v Y izhodi

Graf funkcije
$\begin{align}&\scriptstyle f \colon [-1,1.5] \to [-1,1.5] \\ &\textstyle x \mapsto \frac{(4x^3-6x^2+1)\sqrt{x+1}}{3-x}\end{align}$

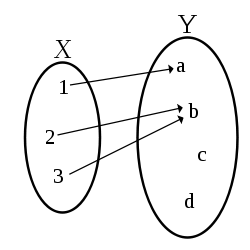
Fúnkcija $f: A \longrightarrow B$ je v matematiki preslikava, ki vsakemu elementu množice A priredi natanko en element množice B.

Če definiramo funkcijo $f: a \longmapsto b$, je a podatek ali original, b pa je funkcijska vrednost oziroma rezultat ali slika. Funkcijsko zvezo lahko krajše zapišemo $b=f(a)$.

Množico vseh originalov (množico A) imenujemo definicijsko območje funkcije - $\mathcal{D}_f$, množico vseh slik pa zaloga vrednosti funkcije - $\mathcal{Z}_f$ (to je v splošnem podmnožica množice B).

Vrste funkcij

Funkcija realne spremenljivke je funkcija, ki ima za podatke realna števila, tj.: $\mathcal{D}_f\subseteq\mathbb{R}$.

Realna funkcija je funkcija, ki ima za rezultate realna števila, tj.: $\mathcal{Z}_f\subseteq\mathbb{R}$.

Realna funkcija realne spremenljivke je funkcija, ki ima za podatke in za rezultate realna števila, tj.: $\mathcal{D}_f\subseteq\mathbb{R},~ \mathcal{Z}_f\subseteq\mathbb{R}$.

Izraz funkcija v ožjem pomenu besede pomeni realna funkcija realne spremenljivke, saj ravno takšne funkcije matematika najpogosteje preučuje. Táko funkcijo lahko tudi ponazorimo z grafom v kartezični ravnini - graf funkcije je množica točk (x,y), za katere velja zveza y = f(x).

Izraz funkcija se v matematiki najpogosteje uporablja v ožjem pomenu (realna funkcija realne spremenljivke), vendar pa včasih to besedo uporabljamo tudi v širšem pomenu - za splošnejše preslikave, npr.:

• realne funkcije naravne spremenljivke, ki se imenujejo tudi zaporedja: $\mathcal{D}_f=\mathbb{N},~ \mathcal{Z}_f\subseteq\mathbb{R}$
• kompleksne funkcije kompleksne spremenljivke, ki imajo za podatke in rezultate kompleksna števila: $\mathcal{D}_f\subseteq\mathbb{C},~ \mathcal{Z}_f\subseteq\mathbb{C}$

Lastnosti funkcij

Funkcija $f: A \longrightarrow B$ je:

• injektivna, če vsak par različnih elementov iz množice A preslika v par različnih elementov v množici B;
• surjektivna, če je vsak element iz množice B slika vsaj enega elementa iz množice A;
• bijektivna, če je injektivna in surjektivna hkrati.

Funkcija f je

• soda funkcija, če za vsak x velja: $f(-x)=f(x)\!\,$
• liha funkcija, če za vsak x velja: $f(-x)=-f(x)\!\,$

Funkcija f je na danem intervalu (a, b)

• naraščajoča , če velja: $x_1 < x_2 \Rightarrow f(x_1) < f(x_2)$
• padajoča, če velja $x_1 < x_2 \Rightarrow f(x_1) > f(x_2)$.

Ničla funkcije je tam, kjer je $f(a) = 0$ oz. kjer se graf funkcije stika s abcisno (vodoravno) osjo.

Glej tudi

• seznam matematičnih funkcij
• preslikava