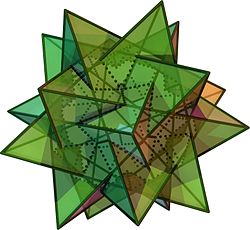
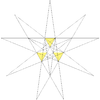
Sestav petih tetraedrov

| |||||||
| Vrsta | pravilni sestav | ||||||
| Sklic | UC5, W24 | ||||||
| Elementi (kot sestav) |
5 tetraedrov: F = 20, E = 30, V = 20 | ||||||
| Dualni sestav | sebi dualen | ||||||
| Simetrijska grupa | kiralna ikozaedrska (I) | ||||||
| Podgrupa omejena na eno komponento | kiralna tetraedrska (T) | ||||||
| |||||||
Sestav petih tetraedrov je v geometriji sestav uniformnih poliedrov stelacija pravilnega ikozaedra. Prvi je sestav opisal Edmund Hess (1843–1903) v letu 1876.
Sklic v preglednici na desni se nanaša na seznam sestavov uniformnih poliedrov.
Sestav[uredi | uredi kodo]
- Prosojni model (animacija)
Lahko se ga naredi tako, da se razporedi pet tetraedrov v vrtilni ikozaedrski simetriji (I), tako kot je to obarvano na desni sliki. Je eden izmed sestavov, ki se jih lahko naredi iz enakih platonskih teles.
Ima isto razvrstitev oglišč kot pravilni dodekaeder.
Znani sta dve enanciomorfni obliki. Od njih ima isto telo nasprotno kiralnost tega sestava poliederskega sestava. Obe obliki tvorita zrcalnosimetrični obliki sestava desetih tetraedrov.
Stelacija[uredi | uredi kodo]
Lahko se ga dobi tudi kot stelacijo ikozaedra. V seznamu modelov Wenningerjevih poliedrov ima oznako (indeks) 24.
Facetiranje[uredi | uredi kodo]
Telo je facetiranje dodekaedra. To je prikazano na naslednji sliki.

Grupna teorija[uredi | uredi kodo]
Kot sestav petih tetraedrov je geometrijski način označevanja orbit in stabilizatorjev, kot je to navedeno v nadaljevanju.
Simetrijska grupa sestava je ikozaedrska grupa reda 60. Stabilizator samo enega tetraedra pa ima tetraedrsko grupo T reda 12. Prostor orbit I/T, z redom 60/12 = 5 se lahko enači s petimi tetraedri.
[uredi | uredi kodo]

Sestav ima nekaj nenavadnih značilnosti. Njegovo dualno telo je enanciomorfna oblika osnovnega telesa. Ta značilnost vodi do zamisli, da ima vsaka kiralna oblika nasprotno kiralnost. To pa ne drži. Vsako dualno telo ima isto kiralnost kot njegov dvojček. Kadar ima polieder desne zavoje, ima njegovo dualno telo tudi desne zavoje.
Telo, ki se ga obravnava, je sestav petih tetraedrov. Kadar so stranske ploskve obrnjene na desno, so oglišča obrnjena na levo. Kadar se dualizira stranske ploskve, ki so desno zasukana oglišča, in se oglišča dualizira v levo zasukane stranske ploskve, se dobi kiralnega dvojčka. So pa telesa s to značilnostjo zelo redka.
Glej tudi[uredi | uredi kodo]
Zunanje povezave[uredi | uredi kodo]
- Weisstein, Eric Wolfgang. »Tetrahedron 5-Compound«. MathWorld.
- Skulpture na Bulatov.org (angleško)
- Pet sekajočih se tetraedrov[mrtva povezava] (angleško)
- Sestav petih tetraedrov na mnogokotniki in poliedri (angleško)
- Sestavi poliedrov (angleško)
| Pomembnejše stelacije ikozaedra | |||||||||
| Pravilni | Uniformni duali | Pravilni sestavi | Pravilne zvezde | Ostali | |||||
| ikozaeder | mali triambski ikozaeder | srednji triambski ikozaeder | veliki triambski ikozaeder | sestav petih oktaedrov | sestav petih tetraedrov | sestav desetih tetraedrov | veliki ikozaeder | izkopani dodekaeder | končna stelacija |
|---|---|---|---|---|---|---|---|---|---|

|

|

|

|

|

|

|

|

| |
|

|

|
|
|

|

|
|

| |
| Postopek stelacije na ikozaedrih ustvari večje število podobnih poliedrov in sestavov z ikozaedersko simetrijo. | |||||||||