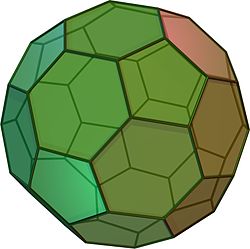
Prisekani ikozaeder

Prisekani ikozaeder
(animacija)
vrsta	arhimedsko telo uniformni polieder
elementi	F = 32, E = 90, V = 60 (χ = 2)
stranske ploskve na stran	12{5} + 20{6}
Conwayjev zapis	tI
Schläflijevi simboli	t{3,5}
	t0,1{3,5}
Wythoffov simbol	2 5 | 3
Coxeter-Dinkinov diagram
simetrija	Ih, H3, [5,3], (*532), red 120
vrtilna grupa	I, [5,3]+, (532), red 60
diedrski kot	6-6: 138,189685º 6-5: 142,62º
sklici	U25, C27, W9
značilnosti	konveksen polpravilen
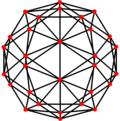
obarvane stranske ploskve	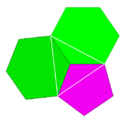5.6.6 (slika oglišč)
pentakisni dodekaeder (dualni polieder)	mreža telesa

Prisekani ikozaeder je v geometriji konveksni polieder. Je arhimedsko telo, eno od trinajstih konveksnih izogonalnih neprizmatičnih teles skonstruirano z dvema ali več vrstami pravilnih mnogokotniških stranskih ploskev.

Ima dvaintrideset pravilnih stranskih ploskev, od tega dvanajst petkotniških in dvajset šestkotniških, ter 90 robov in 60 oglišč.

Konstrukcija

Prisekani ikozaeder se lahko konstruira iz ikozaedra tako, da se odreže 12 oglišč. To se naredi tako, da se odreže eno tretjino na vsakem od obeh koncev roba. To ustvari 12 novih petkotniških stranskih ploskev in pusti 20 prvotnih trikotniških stranskih ploskev kot pravilne šestkotnike. Tako je dolžina nastalih robov ena tretjina prvotnih robov.

Kartezične koordinate

Kartezična koordinate oglišč prisekanega ikozaedra, ki leži v izhodišču, so sode permutacije:

(0, ±1, ±3φ)

(±2, ±(1+2φ), ±φ)

(±1, ±(2+φ), ±2φ)

kjer je φ = (1 + √5) / 2 število zlatega reza. Če se uporabi φ² = φ + 1, se lahko prepriča, da so vsa oglišča na sferi, ki leži v izhodišču in ima kvadrat polmera enak.

Površina in prostornina

Površina P in prostornina V prisekanega ikozaedra z dolžino roba a sta:

$P=\left(20\cdot {\frac {3}{2}}{\sqrt {3}}+12\cdot {\frac {5}{4}}{\sqrt {1+2/{\sqrt {5}}}}\right)a^{2}\approx 72.607253a^{2}\!\,,$

$V={\frac {1}{4}}(125+43{\sqrt {5}})a^{3}\approx 55.2877308a^{3}\!\,.$

Pravokotne projekcije

Prisekani ikozaeder ima pet posebnih pravokotnih projekcij usrediščenih na oglišče, dve vrsti robov in dve vrsti stranskih ploskev (šestkotniki in petkotniki). Zadnji dve odgovarjata Coxeterjevima ravninama A₂ in H₂.

Pravokotne projekcije

usrediščeno na	oglišče	rob 5-6	rob 6-6	stransko ploskev – šestkotnik	stransko ploskev – petkotnik
slika
projektivna simetrija	[2]	[2]	[2]	[6]	[10]
pentakisni dodekaeder

Sorodni poliedri in tlakovanja

Družina uniformnih ikozaederskih poliedrov

{5,3}	t0,1{5,3}	t1{5,3}	t0,1{3,5}	{3,5}	t0,2{5,3}	t0,1,2{5,3}	s{5,3}

simetrija	Sferna				Ravninska	hiperbolična...
	*232 [2,3] D3h	*332 [3,3] Td	*432 [4,3] Oh	*532 [5,3] Ih	*632 [6,3] P6m	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
red	12	24	48	120	∞
prisekane oblike	2.6.6	3.6.6	4.6.6	5.6.6	6.6.6	7.6.6	8.6.6	3.4.∞.4
Coxeter Schläfli	t0,1{3,2}	t0,1{3,3}	t0,1{3,4}	t0,1{3,5}	t0,1{3,6}	t0,1{3,7}	t0,1{3,8}	t0,1{3,∞}
n-kisne oblike	V2.6.6	V3.6.6	V4.6.6	V5.6.6	V6.6.6	V7.6.6
Coxeter

Neuniformni prisekan ikozaeder 2 5 | 3	U37 2 5/2 | 5	U61 5/2 3 | 5/3	U67 5/3 3 | 2	U73 2 5/3 (3/2 5/4)	popolna stelacija
Neuniformni prisekan ikozaeder 2 5 | 3	U38 5/2 5 | 2	U44 5/3 5 | 3	U56 2 3 (5/4 5/2) |
Neuniformni prisekan ikozaeder 2 5 | 3	U32 | 5/2 3 3

Glej tudi

• graf prisekanega ikozaedra
• dodekaeder
• ikozidodekaeder
• prisekani dodekaeder
• prisekani rombski triakontaeder
• fuleren

Zunanje povezave

• Weisstein, Eric Wolfgang. »Truncated Icosahedron«. MathWorld.
• Trirazsežni konveksni uniformni poliedri (glej ti) (angleško)
• Uniformni poliedri (angleško)
• Virtualni poliedri v Encyclopedia of Polyhedra (angleško)