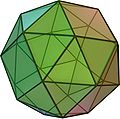
Prirezana kocka
| Prirezana kocka | |
|---|---|
 (animacija) | |
| vrsta | arhimedsko telo uniformni polieder |
| elementi | F = 38, E = 60, V = 24 (χ = 2) |
| stranske ploskve na stran | (8 + 24){3} + 6{4} |
| Conwayjev zapis | sC |
| Schläflijevi simboli | sr{4,3} ali |
| ht0,1,2{4,3} | |
| Wythoffov simbol | | 2 3 4 |
| Coxeter-Dinkinov diagram | |
| simetrija | O, 1/2B3, [4,3]+, (432), red 24 |
| vrtilna grupa | O, [4,3]+, (432), red 24 |
| diedrski kot | 3-3: 153° 14′ 04″ (153,23°) 3-4: 142° 59′ 00″ (142,98°) |
| sklici | U12, C24, W17 |
| značilnosti | konveksna polpravilna kiralna |
 obarvane stranske ploskve |
 3.3.3.3.4 (slika oglišč) |
 petstrani ikozitetraeder (dualni polieder) |
 mreža telesa |
Prirézana kócka (tudi prirézani heksaéder ali prirézani kúboktaéder) je v geometriji konveksni polieder. Je arhimedsko telo, eno od trinajstih konveksnih izogonalnih neprizmatičnih teles skonstruirano z dvema ali več vrstami pravilnih mnogokotniških stranskih ploskev.
Ima osemintrideset pravilnih stranskih ploskev, od tega dvaintrideset enakostraničnotrikotniških in šest kvadratnih, ter 60 robov in 24 oglišč.
Spada med kiralne poliedre z dvema različnima oblikama, ki sta zrcalni sliki (ali enanciomorfni druga drugi). Edini kiralni arhimedski telesi sta prirezana kocka in prirezani dodekaeder.
-
Prva zrcalna oblika
-
Druga zrcalna oblika
Razsežnosti[uredi | uredi kodo]
Prirezana kocka z dolžino roba 1 ima površino . Njena prostornina je enaka , kjer je t tribonacijeva konstanta:
Če ima prvotna prirezana kocka rob z dolžino 1, ima njen dual petstrani ikozitetraeder dolžine roba in .
Kartezične koordinate[uredi | uredi kodo]
Kartezične koordinate oglišč so sode permutacije od
- (±1, ±ξ, ±1/ξ)
s sodim številom pozitivnih predznakov, skupaj z lihimi permutacijami z lihim številom pozitivnih predznakov, kjer je ξ realna rešitev enačbe:
ki se jo lahko piše kot:
- kar je približno 0,43689. ξ je obratna vrednost tribonacijeve konstante. Če se vzame sode permutacije s pozitivnim predznakom in lihe permutacije z negativnim predznakom, se dobi drugačno prirezano kocko, ki je zrcalna slika. Ta prirezana kocka ima robove z dolžino α, ki zadoščajo enačbi:
in se jih lahko zapiše kot:
Za prirezano kocko z enotsko dolžino roba, se uporabljajo naslednje koordinate:
Pravokotne projekcije[uredi | uredi kodo]
Prirezana kocka ima dve posebni pravokotni projekciji usrediščeni na dve vrsti stranskih ploskev (enakostranični trikotniki in kvadrati). Odgovarjata Coxeterjevima ravninama A2 in B2.
| usrediščeno na | rob |
stransko ploskev – enakostranični trikotnik |
stransko ploskev – kvadrat |
|---|---|---|---|
| slika | 
|

|

|
| projektivna simetrija |
[2] | [3] | [4]+ |
| petstrani ikozitetraeder |

|

|

|
Geometrijski odnosi[uredi | uredi kodo]
Prirezano kocko se lahko dobi tako, da se vzame šest stranskih ploskev kocke. Teh šest stranskih ploskev se potegne navzven toliko, da se se več ne dotikajo. Nato se jih malo zavrti okrog njihovih središč (v smeri gibanja urinih kazalcev ali v obratni smeri). To se počneo tako dolgo, da se vmesni prostor napolni z enakostraničnimi trikotniki.
Lahko se jih konstruira tudi s pomočjo alternacije neuniformne kocke. Zbriše se vsa oglišča in se kreira nove trikotnike na mestu zbrisanih oglišč.
 kocka |
 rombikubooktaeder (razširjena kocka) |
 prirezana kocka |
Sorodni poliedri in tlakovanja[uredi | uredi kodo]
Prirezana kocka spada v družino uniformnih poliedrov, ki so povezani s kocko in pravilnim oktaedrom.
| Družina uniformnih oktaedrskih poliedrov | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Simetrija: [4,3], (*432) | [4,3]+ (432) |
[1+,4,3] = [3,3] (*332) |
[3+,4] (3*2) | |||||||
| {4,3} | t{4,3} | r{4,3} r{31,1} |
t{3,4} t{31,1} |
{3,4} {31,1} |
rr{4,3} s2{3,4} |
tr{4,3} | sr{4,3} | h{4,3} {3,3} |
h2{4,3} t{3,3} |
s{3,4} s{31,1} |
= |
= |
= |
||||||||
| Duali uniformnih poliedrov | ||||||||||
| V43 | V3.82 | V(3.4)2 | V4.62 | V34 | V3.43 | V4.6.8 | V34.4 | V33 | V3.62 | V35 |
Ta polpravilni polieder je član zaporedja prirezanega poliedra in tlakovanja s sliko oglišča (3.3.3.3.n) in Coxeter-Dinkinovim diagramom ![]()
![]()
![]()
![]()
![]() . Te oblike in njihovi duali imajo (n32) vrtilno simetrijo.
. Te oblike in njihovi duali imajo (n32) vrtilno simetrijo.
| Simetrija | 232 [2,3]+ D3 |
332 [3,3]+ T |
432 [4,3]+ O |
532 [5,3]+ I |
632 [6,3]+ P6 |
732 [7,3]+ |
832 [8,3]+ |
|---|---|---|---|---|---|---|---|
| red simetrije |
6 | 12 | 24 | 60 | ∞ | ||
| Coxeter Schläfli |
s{2,3} |
s{3,3} |
s{4,3} |
s{5,3} |
s{6,3} |
s{7,3} |
s{8,3} |
| prirezana oblika |
 3.3.3.3.2 |
 3.3.3.3.3 |
 3.3.3.3.4 |
 3.3.3.3.5 |
 3.3.3.3.6 |
 3.3.3.3.7 |
 3.3.3.3.8 |
| prirezana dualna oblika |
 V3.3.3.3.2 |
 V3.3.3.3.3 |
 V3.3.3.3.4 |
 V3.3.3.3.5 |
 V3.3.3.3.6 |
 V3.3.3.3.7 | |
Glej tudi[uredi | uredi kodo]
Zunanje povezave[uredi | uredi kodo]
- Weisstein, Eric Wolfgang. »Snub Cube«. MathWorld.
- Konveksni uniformni poliedri (angleško)
- Uniformni poliedri (angleško)
- Virtualni poliedri v The Encyclopedia of Polihedra (angleško)





![{\displaystyle {\tfrac {1}{3}}\scriptstyle {(1+{\sqrt[{3}]{19-3{\sqrt {33}}}}+{\sqrt[{3}]{19+3{\sqrt {33}}}})\approx 1,83929}\!\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b5f62ab1098b4cb113aa4a317c29977aeddb2b5)



![{\displaystyle \xi ={\frac {1}{3}}\left({\sqrt[{3}]{17+3{\sqrt {33}}}}-{\sqrt[{3}]{-17+3{\sqrt {33}}}}-1\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/737fbacde6c58fa15561c938c9671e63403908ee)

![{\displaystyle \alpha ={\sqrt {{\frac {4}{3}}-{\frac {32}{6{\sqrt[{3}]{2}}\beta }}+{\frac {6{\sqrt[{3}]{2}}\beta }{9}}}}\approx 1,60972\!\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76e04dbc0d0704088386664454ceb4bd5689a026)
![{\displaystyle \beta ={\sqrt[{3}]{13+3{\sqrt {33}}}}\!\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a953ea7aec39be3ae531daef7aa237238755bda)




![{\displaystyle c_{1}={\sqrt[{3}]{3{\sqrt {33}}+17}}\!\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf830f1f0e9d8bb7e43409741a45ae61d8d69986)
![{\displaystyle c_{2}={\sqrt[{3}]{3{\sqrt {33}}-17}}\!\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d02244ba06eff3726764fffec66b331f19091068)
![{\displaystyle c_{3}={\sqrt[{3}]{199+3{\sqrt {33}}}}\!\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d4bfc61be879b0fee366ba38b3f5348c8ba267a)
![{\displaystyle c_{4}={\sqrt[{3}]{199-3{\sqrt {33}}}}\!\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da5ba2865dbac1daff199dec57574881c82c563c)

