Alternacija (geometrija)

Glej rdeče in zelene točke, ki se nahajajo na vsakem drugem oglišču. Prirezana kocka nastane z brisanjem množice oglišč v smeri gibanja urinih kazalcev ali v obratni smeri.
Alternacija (tudi delna prisekanost in prirezanost ali snubifikacija) je v geometriji postopek, ki se izvaja nad poliedri ali tlakovanji. Ta postopek odstrani vsako drugo oglišče. Alternacijo se lahko torej izvede samo na poliedrih, ki imajo sodo število oglišč. Takšen primer so zonoedri. Vsaka 2n-stranska stranska ploskev postane n stranska. Kvadratne stranske ploskve izginejo v nove robove.
Sam postopek alternacije je alterniranje.
Alternacijo pravilnega poliedra ali tlakovanja se včasih označuje s pravilno obliko tako, da se spredaj doda h (iz besede half, ki pomeni polovico). Zgled: oznaka h{4, 3} pomeni alternirano kocko, ki kreira tetraeder. Alternirano kvadratno tlakovanje pa se označi s h{4, 4}.
Snub (snubifikacija, prirezanost)[uredi | uredi kodo]
Snub (prirezanost/potlačenost, snubifikacija) je podobna operacija. To je alternacija uporabljena na omniprisekanem pravilnem poliedru. Omniprisekani pravilni polieder ali tlakovanje ima vedno sodo število stranic in tako se vedno lahko izvede alternacijo.
Zgled je prirezana kocka, ki se jo dobi v dveh korakih. Najprej se izvede omniprisekanost in se dobimo veliki rombikubooktaeder. Nato se polieder z alternacijo pretvori v prirezano kocko.
Naslednji zgled je pravilna antiprizma. Uniformno n-kotno antiprizmo se lahko dobi iz alternirane 2n-kotniške prizme in prirezanega hozoedra z n robovi. V primeru prizem sta obe alternirani obliki enaki.
Alternira se lahko tudi zonoedre. Kot zgled se lahko navede rombski triakontaeder, ki se ga z operacijo snub pretvori v ikozaeder ali dodekaeder, kar je odvisno od izbire odstranjenih oglišč.
Zgledi[uredi | uredi kodo]
Generatorji platonskih teles[uredi | uredi kodo]
Tri oblike: pravilna → omniprisekana → prirezana.
Dani so tudi Coxeter-Dinkinovi diagrami. Omniprisekanost deluje pri vseh zrcalih (obkroženo). Alternacija je prikazana s praznimi obroči.
| simetrija (p q 2) |
pravilni |
omniprisekani |
prirezana oblika |
|---|---|---|---|
| tetraedrska (3 3 2) |
 tetraeder |
 prisekani oktaeder |
 ikozaeder (prirezani tetraeder) |
| oktaedrska (4 3 2) |
 kocka |
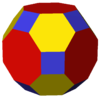 prisekani kubooktaeder |
 prirezana kocka |
| ikozaedrska (5 3 2) |
 dodekaeder |
 prisekani ikozidodekaeder |
 prirezani dodekaeder |
Generatorji pravilnega tlakovanja[uredi | uredi kodo]
| simetrija (p q 2) |
pravilni |
omniprisekani |
prirezana oblika |
|---|---|---|---|
| kvadratno (4 4 2) |
 (4.4.4.4) |
 (4.8.8) |
 (3.3.4.3.4) |
| šestkotno (6 3 2) |
 (6.6.6) |
 (3.4.6.4) |
 3.3.3.3.6 |
Generatorji uniformnih prizem[uredi | uredi kodo]
Za prizme se lahko uporabi izmenična prirezavanja. (kvadratna antiprizma se lahko imenuje hozoeder, kot tudi alternirana osemstrana prizma.)
Dva koraka: 2n-strana prizma → n-strana antiprizma.
- kvadratna prizma → digonalna antiprizma (ali polkocka)
- šeststrana prizma → tristrana antiprizma
- osemstrana prizma → kvadratna antiprizma
- desetkotna prizma → petstrana antiprizma
- ....
Izmenična prisekavanja[uredi | uredi kodo]
Podobni postopki prisekajo izmenjujoča se oglišča in ne samo, da jih odstranijo. V nadaljevanju je našteta množica poliedrov, ki se jih lahko generira iz Catalanovih teles. Ta imajo dve vrsti oglišč, ki se jih lahko izmenoma priseka. Prisekavanje oglišč »višjega reda« in obeh tipov oglišč ustvarja naslednje oblike:
| ime | izvirno telo | prisekano telo | polna prisekanost | ime prisekanosti |
|---|---|---|---|---|
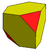
| kocka dual rektificiranega tetraedra |

|
|

|
alternirano prisekana kocka |
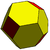
| rombski dodekaeder dual kubooktaedra |
|

|
prisekani rombski dodekaeder | |
| rombski triakontaeder dual ikozidodekaedra |

|

|

|
prisekani rombski triakontaeder |
| triakisni tetraeder dual prisekanega tetraedra |

|

|
prisekani triakisni tetraeder | |
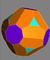
| triakisni oktaeder dual prisekane kocke |

|
|
prisekani triakisni oktaeder | |
| triakisni ikozaeder dual prisekanega dodekaedra |

|
prisekani triakisni ikozaeder |
Višje razsežnosti[uredi | uredi kodo]
Alternacijo se lahko izvede tudi za višjerazsežne politope in satovja. Večina oblik nima splošne rešitve. Praznine, ki pri tem nastanejo, ne kreirajo uniformnih facet. Zgledi:
- satovja
- alternirano kubično satovje je tetraedrsko-oktaedrsko satovje.
- alternirano heksagonalno prizmatično satovje je zavito alternirano satovje.
- polihoroni
- alternirana prisekana 24-celica je prirezana 24-celica.
- hiperkocko se lahko z alternacijo vedno spremeni v uniformno polhiperkocko.
- kocka → tetraeder (pravilni)
 →
→ 
- teserakt (8-celica) → 16-celica (pravilna)
 →
→ 
- penterakt → polpenterakt (polpravilni)
- hekserakt → polhekserakt (uniformni)
- ...
Glej tudi[uredi | uredi kodo]
- Drugi postopki nad uniformnimi politopi:
- Conwayjeva notacija poliedrov
- Wythoffova konstrukcija
- kiralni politop
Zunanje povezave[uredi | uredi kodo]
- Alternacija v Glossary for Hyperspace (angleško)
- Imena poliedrov (angleško)












