Trapezoeder
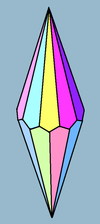
| Množica trapezoedrov | |
|---|---|
| |
| Stranske ploskve | 2n deltoidov |
| Robovi | 4n |
| Oglišča | 2n + 2 |
| Konfiguracija stranskih ploskev | V3.3.3.n |
| Simetrijska grupa | Dnd, [2+,2n], (2*n) reda 4n |
| Vrtilna grupa | Dn, [2,n]+, (22n) reda 2n |
| Dualni polieder | antiprizma |
| Lastnosti | konveksni, tranzitivne stranske ploskve |
Trapezoeder (tudi antidipiramida ali deltoeder) je dualni polieder n-strane antiprizme. Njegove 2-n stranske ploskve so skladni deltoidi.
Dualna n-strana antiprizma ima dve n-strani stranski ploskvi.
Vsak n-strani trapezoeder lahko razbijemo na dve enaki n-strani piramidi in n-strani antiprizmi.
Oblike
[uredi | uredi kodo]Včasih se imenujejo tudi deltoedri. Ne sme pa se jih zamenjevati z deltaedri, ki imajo za stranske ploskve enakostranične trikotnike.
V opisih kristalnih habitov se izraz trapezoeder pogosto uporablja za deltoidni ikozitetraeder.
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ... |
|---|---|---|---|---|---|---|---|---|

|

|

|

|

|
V primeru duala pravilne tristrane antiprizme so deltoidi rombi. Torej so trapezoedri tudi zonoedri. Imenujejo se romboedri. So kocke, ki so umerjene v smeri telesne diagonale. To so tudi paralelepipedi s skladnimi rombskimi stranskimi ploskvami.
Posebni primer romboedra je tisti, v katerem rombi tvorijo stranske ploskve, ki imajo kote 60º in 120º. Lahko se jih razstavi v dva enaka pravilna tetraedra in pravilni oktaeder. Ker pa paralelepipedi lahko zapolnijo prostor, se to lahko naredi tudi s kombinacijo pravilnega tetraedra in pravilnega oktaedra.
Simetrija
[uredi | uredi kodo]Simetrijska grupa n-stranega trapezoedra je Dnd reda 4n. Tega pa ni pri kocki, ki ima višjo simetrijsko grupo Od reda 48. Ta pa ima štiri oblike D3d kot podgrupe.
Vrtilna grupa je Dn reda 2n. Tega pa ni pri kocki, ki ima višjo vrtilno grupo O reda 24. Ta pa ima štiri oblike D3 kot podgrupe.
Zunanje povezave
[uredi | uredi kodo]- Weisstein, Eric Wolfgang. »Trapezohedron«. MathWorld.
- Poliedri v Encyclopedia of Polyhedra (angleško)
- Papirni modeli trapezoedrov (angleško)
- Conwayjeva notacija poliedrov (angleško)

