5-celica
| Pravilna 5-celica (4-simpleks) | |
|---|---|
 Schleglov diagram (oglišča in robovi) | |
| vrsta | |
| Schläflijev simbol | {3,3,3} |
| Coxeter-Dinkinov diagram | |
| celice | 5 {3, 3} |
| ploskve | 10 {3} |
| robovi | 10 |
| oglišča | 5 |
| slika oglišč | 
|
| Petriejev mnogokotnik | petkotnik |
| Coxeterjeva grupa | A4 [3,3,3] |
| dual | sebidualna |
| značilnosti | konveksna, izogonalna, izotoksalna, izohedralna |
| uniformni indeks | 1 |
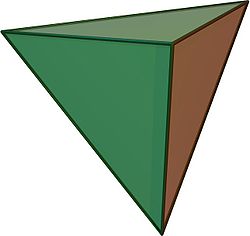
5-celica je štirirazsežni objekt omejen s petimi tetraedrskimi celicami. Znan je tudi kot pentahoron ali pentatop ali hiperpiramida. Je 4-simpleks in je najenostavnejši konveksni pravilni politop in štirirazsežni analog trirazsežnega tetraedra in dvorazsežnega trikotnika.
Projekcije[uredi | uredi kodo]
A4
|
A3
|
A2
| |
Graf
|

|
|

|
[5]
|
[4]
|
[3]
|
| Projekcije v tri razsežnosti | |
|---|---|
 Ogrodje stereografske projekcije (robovi projicirani na 3-sfero) |
 Trirazsežna projekcija 5-celice, ki izvaja enostavno vrtenje |
 Projekcija pentahorona z ogliščem spredaj v 3 razsežnostih ima tetraedersko ovojnico. Najbližje oglišče pentahorona se projicira v središče tetraedra kot je prikazano z rdečo barvo. Najoddaljenejša celica se projicira na tetraedersko ovojnico. Druge 4 celice se projicirajo na 4 raztegnjena tetraederska področja okoli osrednjega oglišča. |
 Projekcija pentahorona s sprednjim robom v 3 razsežnostih ima trikotno bipiramidalno ovojnico. Najbližji rob (prikazan rdeče) se projicira na os dipiramide s tremi celicami, ki ga obkrožajo in projicirajo v 3 tetraederske prostornine, ki so nameščene okoli te osi na vsakih 120º. Ostali dve celici se pojicirata na dve polovici dipiramide in sta na zadnji strani pentatopa. |
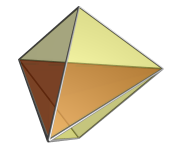 Projekcija pentahorona s stransko ploskvijo spredaj v 3 razsežnosti ima tudi trikotno dipiramidalno ovojnico. Najbližja stranska ploskev je prikazana z rdečo barvo. Po dve celici, ki se dotikata v tej stranski ploskvi, se projicirata na dve polovici dipiramide. Ostale tri celice so na oddaljeni strani pentatopa, če gledamo s stališča štirih razsežnosti in zaradi razumljivosti niso prikazane na sliki. Nameščene so okoli središčne osi dipiramide, prav tako kot pri projekciji z robom spredaj. |
 Projekcija pentahorona s celico spredaj v 3 razsežnosti ima tetraedersko ovojnico. Najbližja projekcija celice na celotno ovojnico. Iz stališča štirih razsežnosti druge 4 celice niso vidne. |
Sorodni uniformni polihoroni[uredi | uredi kodo]
| ime | 5-celica | prisekana 5-celica | rektificirana 5-celica | kantelirana 5-celica | dvojno prisekana 5-celica | kantiprisekana 5-celica | runcinirana 5-celica | runciprisekana 5-celica | omniprisekana 5-celica |
|---|---|---|---|---|---|---|---|---|---|
| Schläflijev simbol |
{3,3,3} | t0,1{3,3,3} | t1{3,3,3} | t0,2{3,3,3} | t1,2{3,3,3} | t0,1,2{3,3,3} | t0,3{3,3,3} | t0,1,3{3,3,3} | t0,1,2,3{3,3,3} |
| Coxeter-Dinkinov diagram |
|||||||||
| Schleglov diagram |

|

|

|

|

|

|

|

|

|
| A4 Coxeterjeva ravnina graf |

|

|

|

|

|

|

|

|

|
| A3 Coxeterjeva ravnina graf |

|

|

|

|

|

|

|

|

|
| A2 Coxeterjeva ravnina graf |

|

|

|

|

|

|

|

|

|
Zunanje povezave[uredi | uredi kodo]
- Weisstein, Eric Wolfgang. »Pentatope«. MathWorld.
- Pentahoron (angleško)
- Pentahoron v Glossary for Hyperspace (angleško)
- Konveksni uniformni polihoroni osnovani na pentahoronu (angleško)
- Der 5-Zeller(nemško)
- Pravilni polihoroni (angleško)

