Heksaeder

Heksaeder je poljubni polieder, ki ima šest stranskih ploskev. Kot zgled je najbolj primerna pravilna kocka, ki ima tri kvadrate okoli vsakega oglišča. To telo je eno izmed heksaedrov s štirimi stranskimi ploskvami. Je tudi posplošitev kocke saj je eden izmed sedmih konveksnih heksaedrov . Pravilni heksaeder je kocka.

Znanih je sedem topološko različnih konveksnih heksaedrov Eden med njimi obstoja v dveh zrcalnih oblikah. Dva poliedra sta "topološko različna" kadar imata različno razporeditev stranskih ploskev in oglišč tako, da ne moremo spremeniti enega v drugega samo s spremembo robov ali kotov med robovi in stranskimi ploskvami. V nadaljevanju za opis stranskih ploskev glej konfiguracija oglišča.

Štirikotniki s stranskimi ploskvami heksaedrov 46 stranskih ploskev, 12 robov, 8 oglišč
paralelepiped (trije pari paralelogramov)	romboeder (trije pari rombov)	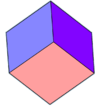tristrani trapezoeder (skladen z rombi)	kvader (trije pari pravokotnikov)	kocka (kvadrat)	štiristrana prisekana piramida (prisekan vrh kvadratne piramide)
Ostali
tristrana bipiramida 36 stranske ploskve 9 E, 5 V	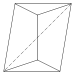štiristrani antiklin. kiralni – obstoja v "levo" in "desno" sučni zrcalni obliki. 4.4.3.3.3.3 stranske ploskve 10 E, 6 V	4.4.4.4.3.3 stranske ploskve 11 E, 7 V	petstrana piramida 5.35 stranske ploskve 10 E, 6 V	5.4.4.3.3.3 stranske ploskve 11 E, 7 V	5.5.4.4.3.3 stranske ploskve 12 E, 8 V

Obstojajo tudi topološko različni heksaedri, ki jih lahko naredimo kot konkavne oblike:

Konkavne oblike
4.4.3.3.3.3 stranske ploskve 10 E, 6 V	5.5.3.3.3.3 stranske ploskve 11 E, 7 V	6.6.3.3.3.3 stranske ploskve 12 E, 8 V

Glej tudi

• prizmatoid

Zunanje povezave

• Poliedri s štirimi do sedmimi stranskimi ploskvami Arhivirano 2006-09-04 na Wayback Machine. (angleško)
• Weisstein, Eric W. »Hexahedron«. MathWorld.
• Elementi heksaedra Arhivirano 2015-11-27 na Wayback Machine. (angleško)
• Pravilni heksaeder (angleško)