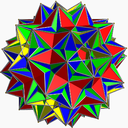
Uniformni zvezdni polieder

Uniformni zvezdni polieder je sebe sekajoč uniformni polieder. Imenujemo ga tudi nekonveksni polieder. Vsak polieder ima stranske ploskve, ki so zvezdni mnogokotniki, imajo za slike oglišč zvezdne mnogokotnike ali oboje.

Polna skupina 57 neprizmatičnih uniformnih poliedrov vključuje 4 pravilne, ki jih imenujemo Kepler-Poinsotovi poliedri, 5 je kvazipravilnih poliedrov in 48 je polpravilnih.

Razen tega obstoja še neskončna množica uniformnih zvezdnih prizem in uniformnih zvezdnih antiprizem. Tako kot neizrojeni zvezdni mnogokotniki, ki imajo mnogokotniško gostoto večjo od 1 in pripadajo krožnim mnogokotnikom s prekrivajočimi se ploščicami, zvezdni poliedri ne potekajo skozi središče in imajo politopsko gostoto večjo od 1, ter odgovarjajo sfernim poliedrom s prekrivajočimi se ploščicami. Obstoja 48 takšnih uniformnih zvezdnih poliedrov. Ostalih 9 neprizmatičnih uniformnih zvezdnih poliedrov, ki tečejo skozi središče, je polpoliedrov in ne odgovarjajo sfernim poliedrom, ker jim ne moremo na enoličen način projicirati središča na sfero.

Nekonveksne oblike se lahko konstruirajo s pomočjo Schwarzovih trikotnikov.

Mali snub ikozikozidodekaeder je uniformni zvezdni polieder s sliko oglišč 3⁵.⁵/₂

(3 3 2) trikotniki na sferi

Diederska simetrija

Glej prizmatični uniformni polieder.

Tetraederska simetrija

(3 3 2) trikotniki na sferi

Obstojata dve nekonveksni obliki. To sta tetrahemiheksaeder in octahemioktaeder, ki imata tetraedersko simetrijo z osnovno domeno Möbiusov trikotnik (3 3 2)).

Obstojata dva Schwarzovih trikotnikov, ki enolično generirajo nekonveksne uniformne poliedre: eden je pravokotni trikotnik (3/2 3 2) in en splošni trikotnik (3/2 3 3).

Razvrstitev oglišč (Konveksna ogrinjača)	Nekonveksne oblike
tetraeder
Rektificiran tetraeder Oktaeder	Tetrahemiheksaeder4.3/2.4.3) 3/2 3 | 2
Prisekan tetraeder
Kanteliran tetraeder (kubooktaeder)	(6.3/2.6.3) 3/2 3 | 3
Omniprisekan tetraeder (Prisekan oktaeder)
Snub tetraeder (Ikozaeder)

Oktaederska simetrija

(4 3 2) trikotniki na sferi

Obstoja 8 konveksnih in 10 nekonveksnih oblik z oktaedersko simetrijo z osnovno domeno Möbiusovega trikotnika (4 3 2)).

Znani so štirje Schwarzovi trikotniki, ki nekonveksne oblike, od tega sta dva za pravokotne trikotnike (3/2 4 2) in (4/3 3 2) ter dva za splošne trikotnike: (4/3 4 3) in (3/2 4 4), ki generirajo nekonveksne oblike.

Razvrstitev oglišč (Konveksna ogrinjača)	Nekonveksne oblike
kocka
oktaeder
kubooktaeder	(6.4/3.6.4) 4/3 4 | 3
prisekana kocka	(4.8/3.4/3.8/5) 2 4/3 (3/2 4/2) |	(8/3.3.8/3.4) 3 4 | 4/3	(4.3/2.4.4) 3/2 4 | 2
prisekan oktaeder
rombikubooktaeder	(4.8.4/3.8) 2 4 (3/2 4/2) |	(8.3/2.8.4) 3/2 4 | 4	(8/3.8/3.3) 2 3 | 4/3
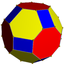Neuniformni prisekan kubooktaeder	(4.6.8/3) 2 3 4/3 |
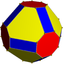Neuniformni prisekan kubooktaeder	(8/3.6.8) 3 4 4/3 |
snub kocka

Ikozaederska simetrija

(5 3 2) trikotniki na sferi

Znanih je 8 konveksnih in 46 nekonveksnih oblik z ikozaedersko simetrijo z osnovno domeno Möbiusovega trikotnika (5 3 2). Nekatere od snub oblik imajo zrcalno ogliščno simetrijo.

Razvrstitev oglišč (Konveksna ogrinjača)	Nekonveksne oblike
ikozaeder	{5,5/2}	{5/2,5}	{3,5/2}
Neuniformni prisekan ikozaeder 2 5 |3	U37 2 5/2 | 5	U61 5/2 3 | 5/3	U67 5/3 3 | 2	U73 2 5/3 (3/2 5/4) |
Neuniformni prisekan ikozaeder 2 5 |3	U38 5/2 5 | 2	U44 5/3 5 | 3	U56 2 3 (5/4 5/2) |
Neuniformni prisekan ikozaeder 2 5 |3	U32 | 5/2 3 3
Icosidodecahedron 2 | 3 5	U49 3/2 3 | 5	U51 5/4 5 | 5	U54 2 | 3 5/2	U70 5/3 5/2 | 5/3	U71 3 3 | 5/3	U36 2 | 5 5/2	U62 5/3 5/2 | 3	U65 5/4 5 | 3
prisekan dodekaeder 2 3 | 5	U42	U48	U63
Neuniformni prisekan dodekaeder	U72
dodekaeder	{5/2,3}	U30	U41	U47
rombiikozidodekaeder	U33	U39	U58
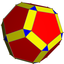Beveled Dodecahedron	U55
Neuniformni rombiikozidodekaeder	U31	U43	U50	U66
Neuniformni rombiikozidodekaeder	U75	U64	Skillingova oblika (glej spodaj)
Neuniformni prisekan ikozidodekaeder	U45
Neuniformni prisekan ikozidodekaeder	U59
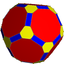Neuniformni prisekan ikozidodekaeder	U68
Neuniformni snub dodekaeder	U40	U46	U57	U69	U60	U74

Skillingova oblika

Eden izmed ostalih nekonveksnih poliedrov je veliki disnub dirombidodekaeder, ki je znan kot Skillingova oblika. Je ogliščno uniformen. Pari robov sovpadajo v prostoru. Štiri stranske ploskve se tako srečajo na istem robu. Ima simetrijo I_h.

Izrojene oblike

Coxeter (1907-2003) je našel večje število izrojenih zvezdnih poliedrov s pomočjo Wythoffove konstrukcije. Ti poliedri vsebujejo prekrivajoče se robove in oglišča. Takšni izrojeni obliki sta:

• mali kompleksni ikozidodekaeder
• veliki kompleksni ikozidodekaeder

Glej tudi

• zvezdni mnogokotnik
• seznam uniformnih poliedrov

Zunanje povezave

• Uniformni polieder na MathWorld (v angleščini)