Zvezdni mnogokotnik
|
|||||||||
| Schläflijev simbol 2<2q<p D(p, q)=1 |
{p/q} | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| oglišča in stranice | p | ||||||||
| Coxeter-Dinkinov diagram |      |
||||||||
| simetrijska grupa | diederska (Dp) | ||||||||
| dualni mnogokotnik | sebi dualni | ||||||||
| notranji kot (stopinj) |
 [1] |
||||||||
Zvezdni mnogokotnik (tudi samo zvezda) je nekonveksni mnogokotnik, ki izgleda kot zvezda.
Vsebina |
Pravilni zvezdni mnogokotniki [uredi]
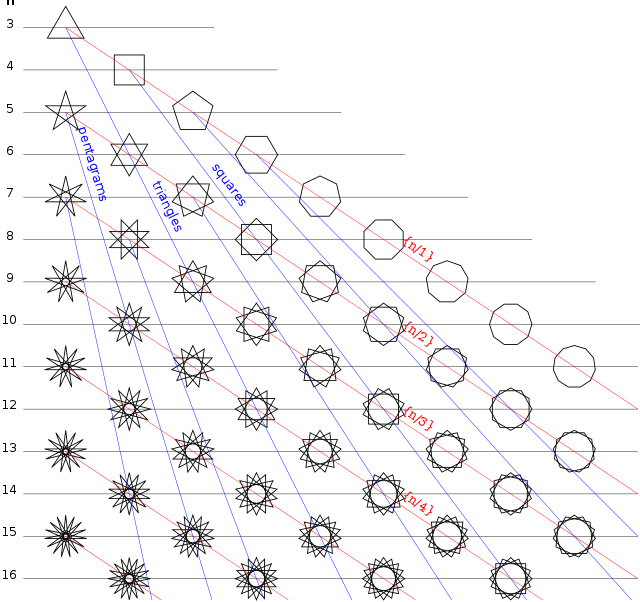
Pravilni zvezdni mnogokotnik je sebe sekajoč enakostraničen in enakokoten mnogokotnik. Dobimo ga tako, da eno oglišče enostavnega in pravilnega p-mnogokotnika z drugim ogliščem, ki pa ni sosednje oglišče mnogokotnika. To nadaljujemo tako dolgo, da se vrnemo v začetno oglišče[2]. Lahko tudi rečemo, da za cela števila p in q zvezdni poligon naredimo tako, da povežemo vsako q-to točko izmed vseh p točk, ki so enakomerno in krožno razporejene [3] Za primer si poglejmo pravilni petkotnik. Petkrako zvezdo dobimo, če potegnemo črto od prvega do tretjega oglišča in od tretjega do petega in od tega do drugega, od tega do četrtega in nato do prvega. Schläflijev simbol za takšno vrsto mnogokotnika je {p/q}, kar je enako kot {p/p-q}. Pravilne zvezdne mnogokotnike dobimo, če sta p in q tuji števili. Pravilni mnogokotnik lahko prikažemo tudi kot stelacijo konveksnega osnovnega mnogokotnika.
 |
Oblike zvezd [uredi]
Če je število stranic n deljivo z m, se zvezdni mnogokotnik dobi iz pravilnega mnogokotnika , ki ima n/m stranic. Nova mnogokotniška zvezda se dobi tako, da zavrtimo pravilni n/m-kotnik v levo glede na začetni mnogokotnik tako, da je število vrtenj oglišč enako n/m zmanjšano za ena. Na koncu še kombiniramo vse nastale slike. Skrajni primer tega nastopi v primeru, da je n/m enako 2. To povzroči nastanek slike, ki jo sestavlja n/2 ravnih delov. To imenujemo degenerirani zvezdni mnogokotnik.
Kadar pa imata n in m skupni faktor, dobimo zvezdni mnogokotnik za nižji n.
Simetrija [uredi]
Simetrijska grupa za {n/k} je diederska grupa Dn reda 2n neodvisno od vrednosti k.
Nepravilni zvezdni mnogokotniki [uredi]
Zvezdni mnogokotniki so lahko tudi nepravilni. Nepravilni zvezdni mnogokotniki nastanejo kot slike oglišč uniformnih poliedrov, ki so določeni z zaporedjem stranskih ploskev okoli vsakega oglišča.
Unikursalni heksagram je naslednji primer cikličnega nepravilnega zvezdnega mnogokotnika. Ima samo D2h diedersko simetrijo.
Opombe in sklici [uredi]
- ^ Kappraff, Jay (2002). Beyond measure: a guided tour through nature, myth, and number. World Scientific. Str. 258. ISBN 9789810247027. http://books.google.com/books?id=vAfBrK678_kC&pg=PA256&dq=star+polygon.
- ^ Coxeter, Harold Scott Macdonald (1973). Regular polytopes. Courier Dover Publications. ISBN 9780486614809.
- ^ Zvezdni mnogokotniki na MathWorld
Glej tudi [uredi]
Zunanje povezave [uredi]
- Zvezdni mnogokotnik na MathWorld (v angleščini)
- Poligram na MathWorld (v angleščini)
- Aplet za prikazovanje zvezdnih mnogokotnikov (v nemščini)
- Zvezdni mnogokotniki (v ruščini)
- Zvezdni mnogokotnik na 2dcurves.com (v angleščini)
|
|||||||||||||||||||||||||||||
