Sedemkotnik

Pravilni sedemkotnik

Nepravilni preprosti sedemkotnik

Sédemkótnik ali sedmerokótnik ali s tujko héptagon (starogrško heptagōnos, iz hepta – sedem in gōnos – tak, ki ima kote) je v ravninski geometriji mnogokotnik s sedmimi stranicami, sedmimi oglišči in sedmimi notranjimi koti.

Sedemkotnik včasih imenujejo tudi septagon, kjer je predpona sept- (elizija številčne predpone septua-, izvedene iz latinščine).

Splošne lastnosti

V pravilnem sedemkotniku so vse stranice in koti enaki, notranji kot pa znaša $5\pi /7\!\,$ radianov, oziroma 128 4/7 = 128,5714286... stopinj. Vsota notranjih kotov v preprostem sedemkotniku je enaka:

$S_{7}=(7-2)\cdot 180^{\circ }=900^{\circ }\!\,.$

Njegov Schläflijev simbol je {7}.

Dolžina stranice $a\!\,$ je:

$a=2R\sin {\frac {\pi }{7}}\approx 0,86777R\!\,,$

kjer je $R\!\,$ polmer očrtane krožnice.

Obseg

Obseg sedemkotnika z dolžino stranice $a\!\,$ je:

$o=7a\!\,.$

Ploščina

Ploščina pravilnega sedemkotnika z dolžino stranice $a\!\,$ je:

$p={\frac {7}{4}}a^{2}\,\operatorname {ctg} \,{\frac {\pi }{7}}\approx 3,63391a^{2}\!\,.$

To se lahko vidi, če se razdeli sedemkotnik s stranico dolžine 1 na sedem trikotniških rezin z vrhovi v središču in ogliščih sedemkotnika, potem pa se vsak trikotnik s pomočjo apoteme kot skupne stranice razdeli na pol. Dolžina apoteme je polovica kotangensa $\pi /7\!\,$, ploščina vsakega od 14-ih majhnih trikotnikov je 1/4 dolžine apoteme.

Točen algebrski izraz prek kubičnega polinoma $x^{3}+x^{2}-2x\!\,$ (ena od njegovih ničel je $2\cos \,(2\pi /7)\!\,$) je dan z:

$p={\frac {1}{4}}{\sqrt {{\frac {7}{3}}\left(35+2{\sqrt[{3}]{196(13-3i{\sqrt {3}})}}+2{\sqrt[{3}]{196(13+3i{\sqrt {3}})}}\right)}}a^{2}\!\,,$

kjer je $i\!\,$ imaginarna enota.

Ploščina pravilnega sedemkotnika s polmerom očrtane krožnice $R\!\,$ je:

$p={\frac {7}{2}}R^{2}\sin {\frac {2\pi }{7}}\approx 2,73641R^{2}\!\,.$

Ploščina očrtanega kroga je $\pi R^{2}\!\,$, tako da ga pravilni sedemkotnik napolni približno za vrednost:

${\frac {7\sin {\frac {2\pi }{7}}}{2\pi }}\approx 0,87103\!\,.$

Drugo

  pravilni sedemkotnik $a\!\,$

  kratke diagonale $a_{1}\!\,$

  dolge diagonale $a_{2}\!\,$

Vsak od štirinajst skladnih sedemkotniških trikotnikov ima eno zeleno, eno modro in eno rdečo stranico.

V pravilni sedemkotnik se lahko včrta 35 različnih trikotnikov, katerih oglišča so tudi oglišča sedemkotnika, kar je enako številu kombinacij brez ponavljanja:

$n_{3}=C_{7}^{3}={\frac {7!}{3!(7-3)!}}={\frac {7!}{3!\cdot 4!}}={\frac {7\cdot 6\cdot 5}{3!}}={\frac {7\cdot 6\cdot 5}{3\cdot 2}}=7\cdot 5=35\!\,.$

• od tega jih je štirinajst znanih kot sedemkotniški trikotniki, ki so vsi skladni s koti $\pi /7\!\,$, $2\pi /7\!\,$ in $4\pi /7\!\,$. Njihove stranice so enake stranici, dolgi in kratki diagonali sedemkotnika. So tudi edini trikotniki s koti v razmerju 1 : 2 : 4. (Glej § Diagonali in sedemkotniški trikotnik)
• sedem trikotnikov ima dve stranici enaki stranicama sedemkotnika in eno kratki diagonali.
• sedem trikotnikov ima eno stranico enako stranici sedemkotnika in dve stranici enaki dolgima diagonalama sedemkotnika.
• sedem trikotnikov ima eno stranico enako dolgi diagonali in dve stranici enaki kratkima diagonalama.

Konstrukcije

Pravilnega sedemkotnika se ne da skonstruirati z ravnilom in šestilom. Obstaja pa več približnih geometrijskih konstrukcij. Ker je 7 Pierpontovo praštevilo, ne pa tudi Fermatovo praštevilo, se pravilnega sedemkotnika ne da skonstruirati z neoznačenim ravnilom in šestilom, ga je pa mogoče skonstruirati z označenim ravnilom in šestilom. Je najmanjši pravilni mnogokotnik s to lastnostjo. Ta vrsta konstrukcije se imenuje konstrukcija nevsis, oziroma konstrukcija vstavljanja. Skonstruirati ga je mogoče tudi s šestilom, neoznačenim ravnilom in trisektorjem kotov (Pierpont-Gleasonov izrek). Nezmožnost konstrukcije z neoznačenim ravnilom in šestilom izhaja iz opažanja, da je $2\cos \,(2\pi /7)\approx 1,247\!\,$ ničla nerascepne kubične funkcije $x^{3}+x^{2}-2x-1\!\,$. Posledično je ta polinom minimalni polinom števila $2\cos \,(2\pi /7)\!\,$, medtem ko mora biti stopnja minimalnega polinoma za konstruktabilno število potenca števila 2.

Konstrukcija nevsis notranjega kota v pravilnem sedemkotniku.

Animacija iz konstrukcije nevsis s polmerom očrtane krožnice $R={\overline {OA}}=6\!\,$, po Andrewu Matteiju Gleasonu, ki temelji na tretjinjenju kota s pomočjo tomahavka. Ta konstrukcija temelji na dejstvu, da je: $6\cos {\frac {2\pi }{7}}=2{\sqrt {7}}\cos \left({\frac {1}{3}}\arctan \left(3{\sqrt {3}}\right)\right)-1\!\,.$

Sedemkotnik z dano dolžino stranice:
Animacija iz konstrukcije nevsis z označenim ravnilom po Davidu Johnsonu Leisku (Crockettu Johnsonu).

Približek

Približek za praktično uporabo z napako približno 0,2 % je uporaba polovice stranice enakostraničnega trikotnika, včrtanega v isto krožnico kot dolžina stranice pravilnega sedemkotnika. Ni znano, kdo je prvi odkril ta približek, vendar ga je omenil Heron Aleksandrijski v svoji Metrici v 1. stoletju, bil je dobro znan srednjeveškim islamskim matematikom – to konstrukcijo je poznal Abul Vefa (940–998). Približek je mogoče najti v delu Leonarda da Vincija (1452–1519), Albrechta Dürerja (1471–1528) in Francoisa Vièta (1550–1603). Naj $A\!\,$ leži na obodu očrtane krožnice. Nariše se lok $BOC\!\,$. Potem $BD=(1/2)BC\!\,$ poda približek za rob sedemkotnika.

Ta približek uporablja ${\sqrt {3}}/2\approx 0,86603\!\,$ za stranico sedemkotnika včrtanega v enotsko krožnico, točna vrednost pa je $2\sin(\pi /7)\approx 0,86777\!\,$.

Zgled za ponazoritev napake:

Pri polmeru očrtane krožnice $R=1\,\mathrm {m} \!\,$ bi bila absolutna napaka prve stranice približno -1,7 mm.

Drugi približki

Obstajajo tudi drugi približki sedemkotnika z uporabo šestila in ravnila, vendar je njihovo risanje zamudno.

Plemljeva konstrukcija

Josip Plemelj je leta 1882 še kot dijak odkril svojo izvirno konstrukcijo pravilnega sedemkotnika. Po njem je delitev krožnice na sedem delov odvisna od rešitev enačbe:

${\frac {x^{7}-1}{x-1}}=0\!\,.$

Koreni te enačbe so $e^{2k\pi i/7}\!\,$, kjer se vstavi $k=1,2,3,\ldots ,6\!\,$. Koren $e^{6\pi i/7}=-e^{-\pi i/7}\!\,$ se označi z $\zeta \!\,$. Količine $\zeta +\zeta ^{-1},\zeta ^{2}+\zeta ^{-2},\zeta ^{4}+\zeta ^{-4}\!\,$ so koreni enačbe:

$y^{3}+y^{2}-2y-1=0\!\,.$

Najprej je s substitucijo $y=2(1-2\sin ^{2}(\pi /7))=2-s^{2}\!\,$ v zadnji enačbi našel enačbo šeste stopnje, ki ustreza stranici pravilnega sedemkotnika $a\!\,$, včrtanega v krožnico s polmerom $R\!\,$:

$(2-s^{2})^{3}+(2-s^{2})^{2}-2(s-s^{2})-1=0\!\,,$

oziroma:

$s^{6}-7s^{4}+14s^{2}-7=0\!\,.$

Dobil je dolžino stranice:

$a={\frac {R{\sqrt {3}}}{2\cos {\frac {\alpha }{3}}}},\qquad \operatorname {tg} {\frac {\alpha }{3}}={\frac {1}{3{\sqrt {3}}}}\ \Rightarrow \alpha \approx 3,6311315^{\circ }=3^{\circ }37'52,0735789''\!\,,$

oziroma:

$a={\frac {R{\sqrt {3}}\sec {\frac {\alpha }{3}}}{2}},\qquad \operatorname {ctg} {\frac {\alpha }{3}}=3{\sqrt {3}}\!\,,$

kjer je $\alpha \!\,$ kot med višino enakostraničnega trikotnika včrtanega v enotsko krožnico (${\sqrt {3}}/2\!\,$) in daljico od nasprotnega ogljišča $C\!\,$ do točke $F\!\,$, ki tretjini daljico od presečišča višine $D\!\,$ do točke $E\!\,$ ($1/6\!\,$, če je stranica trikotnika $a=1\!\,$), ki tretjini daljico $a\!\,$ tega trikotnika. Ta kot se imenuje tudi Plemljev kot.

Plemelj je menil, da je tako enostavna konstrukcija pravilnega sedemkotnika že znana, zato je ni takoj objavil. Rešitve ni našel tudi v knjigi Konstruktionen und Approximationen in systematischer Darstellung Theodorja Vahlena iz leta 1911 in je svojo rešitev objavil leta 1912 v članku Sedminjenje kroga (Die Siebenteilung des Kreises) v tedanji reviji Monatshefte für Mathematik und Physik.

Simetrija

Simetrije pravilnega sedemkotnika. Oglišča so pobarvana glede na njihove simetrijske lege. Modre premice zrcaljenj so narisane skozi oglišča in stranice. Redi giracij so podani v središču.

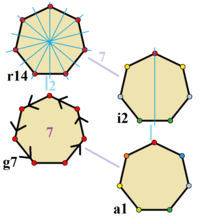
Pravilni sedemkotnik pripada točkovni grupi D_7h (Schoenfliesov zapis), reda 28. Elementi simetrije so: 7-kratna lastna rotacijska os C₇, 7-kratna neprava rotacijska os S₇, 7 navpičnih zrcalnih ravnin σ_v, 7 2-kratnih rotacijskih osi C₂ v ravnini sedemkotnika in vodoravna zrcalna ravnina σ_h, prav tako v ravnini sedemkotnika. Ker je 7 praštevilo, obstaja ena podgrupa z diedrsko simetrijo: Dih₁, in 2 simetriji ciklične grupe: Z₇ in Z₁.

Te 4 simetrije se lahko vidijo v 4-h različnih simetrijah sedemkotnika. Conway jih je označil s črko in z redom grupe. Polna simetrija pravilne oblike je r14 in nobena simetrija ni označena z a1. Diedrske simetrije so razdeljene glede na to ali potekajo skozi oglišča (d za diagonalo) ali stranice (p za pravokotnice), in i kadar premice zrcaljenj potekajo skozi oglišča in stranice. Ciklične simetrije v srednjem stolpcu so označene z g za njihove središčne redove giracij.

Vsaka simetrija podgrupe dovoljuje eno ali več prostostnih stopenj za nepravilne oblike. Le podgrupa g7 nima prostostnih stopenj in se jo ima lahko za usmerjene stranice.

Diagonali in sedemkotniški trikotnik

V pravilnem sedemkotniku za stranico $a\!\,$, krajšo diagonalo $a_{1}\!\,$ in daljšo diagonalo $a_{2}\!\,$, kjer je $a<a_{1}<a_{2}\!\,$ velja:

$a^{2}=a_{2}(a_{2}-a_{1})\!\,,$

$a_{1}^{2}=a(a_{2}+a)\!\,,$

$a_{2}^{2}=a_{1}(a+a_{1})\!\,,$

${\frac {1}{a}}={\frac {1}{a_{1}}}+{\frac {1}{a_{2}}}\!\,$ (optična enačba)

in tako:

$aa_{1}+aa_{2}=a_{1}a_{2}\!\,,$

ter:

$a_{1}^{3}+2a_{1}^{2}a_{2}-a_{1}a_{2}^{2}-a_{2}^{3}=0\!\,,$

$a_{2}^{3}-2a_{2}^{2}a-a_{2}a^{2}+a^{3}=0\!\,,$

$a^{3}-2a^{2}a_{1}-aa_{1}^{2}+a_{1}^{3}=0\!\,.$

Tako koeficienti $-a_{1}/a_{2}\!\,$, $a_{2}/a\!\,$ in $a/a_{1}\!\,$ vsi zadoščajo kubični enačbi $t^{3}-2t^{2}-t+1=0\!\,$. Vendar pa za rešitve te enačbe ne obstajajo algebrski izrazi s čisto realnimi členi, ker je to primer casus irreducibilis.

Približni dolžini diagonal glede na stranico pravilnega sedemkotnika sta podani z:

$a_{1}\approx 1,80193\cdot a,\qquad a_{2}\approx 2,24698\cdot a\!\,.$

Velja tudi

$a_{1}^{2}-a^{2}=aa_{2}\!\,,$

$a_{2}^{2}-a_{1}^{2}=aa_{1}\!\,,$

$a^{2}-a_{2}^{2}=-a_{1}a_{2}\!\ ,$

in:

${\frac {a_{1}^{2}}{a^{2}}}+{\frac {a_{2}^{2}}{a_{1}^{2}}}+{\frac {a^{2}}{a_{2}^{2}}}=5\!\,.$

Sedemkotniški trikotnik ima oglišča, ki sovpadajo s prvim, drugim in četrtim ogliščem pravilnega sedemkotnika (iz poljubnega začetnega oglišča), in kote $\pi /7\!\,$, $2\pi /7\!\,$ in $4\pi /7\!\,$. Tako se njegove stranice ujemajo z eno stranico in dvema posebnima diagonalama pravilnega sedemkotnika.

V poliedrih

Razen sedemstrane prizme in sedemstrane antiprizme noben konveksni polieder, sestavljen v celoti iz pravilnih mnogokotnikov, ne vsebuje sedemkotnika kot ploskve.

Zvezdna sedemkotnika

Iz pravilnih sedemkotnikov se lahko sestavi dve vrsti zvezdnih sedemkotnikov (heptagramov), označenih s Schläflijevema simboloma {7/2} in {7/3}, pri čemer je delitelj interval povezave.

Moder, {7/2} in zelen {7/3} zvezdni sedemkotnik (heptagram) znotraj rdečega sedemkotnika.

Pokritja in pakiranja

Najgostejše znano pokritje evklidske ravnine s pravilnimi sedemkotniki, ki so usmerjeni na dva načina (obarvano različno). Tapetna grupa takšnega pokritja je pmg (22*)

Enakostranični trikotnik, pravilna sedemkotnik in 42-kotnik imajo lahko v ravnini enake dolžine stranic in hkrati skupno oglišče

Poincaréjev krožni model sedemkotniškega pokritja hiperbolične ravnine

Sedemkotnik pravilno ne pokrije evklidske ravnine v celoti in največja gostota pokritja je enaka:

${\frac {2}{97}}\left(-111+492\cos \left({\frac {\pi }{7}}\right)-356\cos ^{2}\left({\frac {\pi }{7}}\right)\right)=0,89269068\ldots \!\,.$

Sedemkotnik lahko pokrije hiperbolično ravnino, kot je razvidno v Poincaréjevem krožnem modelu.

Enakostranični trikotnik, pravilna sedemkotnik in 42-kotnik lahko popolnoma zapolnijo oglišče ravnine. Vendar pa ni mogoče pokriti ravnine samo s temi mnogokotniki, ker ni mogoče enega od njih namestiti na tretjo stranico trikotnika, ne da bi se pri tem pustila vrzel ali ustvarilo prekrivanje. V hiperbolični ravnini so možna pokritja s pravilnimi sedemkotniki. V evklidski ravnini so možna tudi konkavna sedemkotniška pokritja.

Pravilni sedemkotnik ima dvojno rešetkasto pakiranje evklidske ravnine z gostoto pakiranja približno 0,89269068... Domneva se, da je to najnižja možna gostota za optimalno dvojno rešetkasto gostoto pakiranja poljubne konveksne množice in na splošno za optimalno gostoto pakiranja poljubne konveksne množice.

Empirični zgledi

Zambijski kovanec za 1000 kvač (ZMW) je pravi sedemkotnik. Mnoge države za nekatere svoje kovance uporabljajo Reuleauxov sedemkotnik, krivuljo konstantne širine – stranice so ukrivljene navzven, da se kovanci gladko kotalijo, ko se jih vstavi v prodajni avtomat. Mednje spadajo:

• petdeset in dvajset penijev Združenega kraljestva (in ustrezni kovanci na otokih Jersey, Guernsey in Man, v Gibraltarju, na Falklandskih otokih in Sveti Heleni)
• barbadoški dolar (BBD)
• bocvanska pula (2 puli, 1 pula, 50 theb in 5 theb, BWP)
• mavricijska rupija (MUR)
• dirham ZAE (AED)
• tanzanijski šiling (TZS)
• samoanska tala (WST)
• papuanska kina (PGK)
• saotomejska dobra (STD)
• haitski gurd (HTG)
• jamajški dolar (JMD)
• liberijski dolar (LRD)
• ganski cedi (GHS)
• gambijski dalasi (GMD)
• jordanski dina (JOD)
• gvajanski dolar (GYD)
• salomonovootoški dolar (SMD)

Brazilski kovanec za 25 centavov ima v svojem disku vgraviran sedemkotnik. Nekatere stare različice gruzijskega grba, vključno s tistimi iz sovjetskih časov, so kot element uporabljale heptagram {7/2}.

Mnogi kovanci, vključno s kovancem za 20 evrskih centov, imajo sedemkotniško simetrijo v obliki, imenovani španski cvet.

V arhitekturi so sedemkotniški tlorisi zelo redki. Izjemen primer je Mavzolej princa Ernsta v Stadthagnu v Nemčiji.

Mnoge policijske značke v ZDA imajo obris heptagrama {7/2}.

Galerija

• 
  Geometrijski problem ploščine sedemkotnika razdeljenega na trikotnike na glineni ploščici, ki je pripadala šoli za pisanje, Susa, prva polovica 2. tisočletja pr. n. št.
• 
  Slaščica iz Ayerbeja
• 
  Dvorazsežni načrt sedemkotniške fortifikacije, Alain Manesson Mallet, Les Travaux de Mars ou l'Art de la Guerre, 1696
• 
  Sedemkotniška kupola Mavzoleja princa Ernsta
• 
  Sedemkotnik na kaktusu
• 
  Sedemkraka zvezda na cistercijanskem samostanu Beaulieu-en-Rouergue v Ginalsu
• 
  Pečat Avtocestne patrulje Kalifornije (CHP)

Glej tudi

• heptagram
• sedemkotniški trikotnik
• sedemkotniško število
• sedemstrana prizma
• mnogokotnik

Viri

• Altintas, Abdilkadir (2016), »Some Collinearities in the Heptagonal Triangle« (PDF), Forum Geometricorum, 16: 249–256, ISSN 1534-1178, Zbl 1347.51001, arhivirano iz prvotnega spletišča (PDF) dne 13. avgusta 2016, pridobljeno 14. septembra 2025
• Baez, John Carlos (15. november 2014), »Packing Regular Heptagons«, blogs.ams.org (v angleščini), pridobljeno 8. junija 2016
• Bankoff, Leon; Garfunkel, Jack (Januar 1973), »The heptagonal triangle«, Mathematics Magazine, 46 (1): 7–19
• Conway, John Horton; Burgiel, Heidi; Goodman-Strauss, Chaim (2008), »20, Generalized Schaefli symbols, Types of symmetry of a polygon«, The Symmetries of Things, str. 275–278, COBISS 29751813, ISBN 978-1-56881-220-5
• Gleason, Andrew Mattei (Marec 1988), »Angle trisection, the heptagon, and the triskaidecagon« (PDF), The American Mathematical Monthly, 95 (3): 185–194, doi:10.2307/2323624, eISSN 1930-0972, ISSN 0002-9890, JSTOR 2323624, arhivirano iz prvotnega spletišča (PDF) dne 19. decembra 2015
• Hladnik, Milan (september 2013), »Josip Plemelj in pravilni sedemkotnik«, Obzornik za matematiko in fiziko, 60 (5): 161–172, COBISS 16830041, ISSN 0473-7466 – prek Digitalna knjižnica Slovenije{{citation}}: Vzdrževanje CS1: samodejni prevod datuma (povezava)
• Hladnik, Milan (2014), »Nekatere zgodovinske konstrukcije pravilnega sedemkotnika«, Obzornik za matematiko in fiziko, 4: 132–145, COBISS 17178969, ISSN 0473-7466 – prek Digitalna knjižnica Slovenije
• Hogendijk, Jan P. (1987), »Abu'l-Jūd's Answer to a Question of al-Bīrūnī Concerning the Regular Heptagon« (PDF), Annals of the New York Academy of Sciences, 500 (1): 175–183, doi:10.1111/j.1749-6632.1987.tb37202.x, eISSN 1749-6632, ISSN 0077-8923
• Hughes, Gordon H. (2012), The Polygons of Albrecht Dürer-1525, arXiv:1205.0080
• Kallus, Yoav (2015), »Pessimal packing shapes«, Geometry & Topology, 19 (1): 343–363, arXiv:1305.0289, doi:10.2140/gt.2015.19.343, eISSN 1364-0380, ISSN 1465-3060, MR 3318753
• Kuzman, Boštjan (2023–2024), »Heron iz Aleksandrije, Josip Plemelj in skoraj pravilni sedemkotnik«, Presek, 51 (3): 29–31, COBISS 180443651, ISSN 0351-6652 – prek Digitalna knjižnica Slovenije
• Plemelj, Josip (1. december 1912), »Die Siebenteilung des Kreises« [Sedminjenje kroga], Monatshefte für Mathematik und Physik, 23: 309–311, doi:10.1007/BF01707695, eISSN 1436-5081, ISSN 0026-9255
  • Plemelj, Josip (1954), »Pravilni sedmerokotnik« (PDF), Obzornik za matematiko in fiziko, 3 (5–6): 134–135, COBISS 6430809, ISSN 0473-7466, prevod Niko Prijatelj, pridobljeno 14. septembra 2025
• Razpet, Marko (september 2018), Plemljeva najplodnejša leta in časopisje (PDF), Oddelek za matematiko in računalništvo, Pedagoška fakulteta, Univerza v Ljubljani, COBISS 12174409, pridobljeno 14. septembra 2025{{citation}}: Vzdrževanje CS1: samodejni prevod datuma (povezava)
• Salthouse, J. A; Ware, M. J. (1972), Point group character tables and related data, Cambridge: Cambridge University Press, ISBN 0-521-08139-4
• TavianCLirette, ur. (4. avgust 2025), »Heptagon«, Polytope Wiki (v angleščini), pridobljeno 14. septembra 2025

Zunanje povezave

• Weisstein, Eric Wolfgang. »Heptagon«. MathWorld (v angleščini).
• Weisstein, Eric Wolfgang. »Regular Heptagon«. MathWorld (v angleščini).
• Richeson, Dave (23. marec 2016), »A Geometry Theorem Looking for a Geometric Proof«, divisbyzero.com (v angleščini)