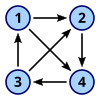
Usmerjeni graf

Usmerjeni graf
Usmerjeni graf.
Povezave	v - 1
Kromatično število	2

Usmerjeni graf ali digraf (di izhaja iz angleške besede directed, kar pomeni usmerjeno) je par $G=(V,A)\,$, kjer je:

• $V\,$ množica vozlišč
• $A\,$ urejeni par vozlišč, ki se imenujejo loki ali usmerjene povezave, včasih se imenujejo tudi kar puščice. Nekateri usmerjene grafe imenujejo tudi enostavni digrafi, da ga tako razlikujejo od usmerjenega multigrafa. V multigrafu povezave tvorijo večkratne množice in ne množice urejenih parov vozlišč. V enostavnem grafu so dovoljene tudi zanke. To so povezave, povezujejo vozlišča s samim seboj.

Lok, ki je usmerjen od $x\,$ proti $y\,$, se označuje z $e=(x,y)\,$. V tem primeru se $x\,$ imenuje glava, $y\,$ pa je rep.

Kadar se lahko neposredno pride od prvega ($x\,$) do drugega ($y\,$) zaporednega vozlišča, se vozlišče $x\,$ imenuje predhodnik, vozlišče $y\,$ pa je naslednik. Lok, ki ima obratno smer, je obrnjeni lok. Graf se imenuje simetričen, če grafu $G\,$ pripadajo tudi vsi obrnjeni loki grafa.

Temeljni graf

Temeljni graf se dobi, če se v digrafu vse usmerjene povezave nadomesti z neusmerjenimi (odstrani se vse usmeritve).

Vhodna in izhodna stopnja

Vhodna stopnja (oznaka $deg^{-}(x)\,$) je število povezav, ki se končajo v $x\,$. Izhodna stopnja (oznaka $deg^{+}(x)\,$) je število povezav, ki se pričnejo v $x\,$. Vozlišče z $deg^{-}(v)=0\,$ se imenuje izvor, vozlišče z $deg^{+}(v)=0\,$, pa se imenuje ponor.

Za vhodno in izhodno stopnjo (če je v grafu končno število vozlišč) velja:

$\sum _{v\in V}\deg ^{+}(v)=\sum _{v\in V}\deg ^{-}(v)\!\,.$

Kadar za vsako vozlišče $v\epsilon V\,$ velja $\deg ^{+}(v)=\deg ^{-}(v)$, se graf imenuje uravnoteženi graf.

Usmerjeni neciklični graf

Turnir s štirimi vozlišči.

Vrste usmerjenih grafov

Usmerjeni neciklični graf je graf, ki nima usmerjenih ciklov.

Turnir je orientirani graf, ki se ga dobi tako, da se izbere smer povezave v neusmerjenem polnem grafu.

Zunanje povezave

• Usmerjeni grafi (slovensko)
• Usmerjeni grafi (angleško)
• Poglavje 10 – usmerjeni grafi Arhivirano 2010-04-13 na Wayback Machine. (angleško)
• Weisstein, Eric Wolfgang. »Oriented Graph«. MathWorld.
• Usmerjeni graf Arhivirano 2008-10-06 na Wayback Machine. na PlanetMath (angleško)
• Značilnosti digrafov (angleško)