Podgrupa
Podgrupa dane grupe za neko dvočleno operacijo * je H podmnožica množice G se imenuje podgrupa G, če H tudi tvori grupo za dvočleno operacijo *. Če smo bolj natančni je H je podgrupa množice G, če so omejitve, ki veljajo za * H x H grupna operacija za H. To se pogosto piše kot H ≤ G, in bere kot "H je podgrupa za G".
Osnovne značilnosti podgrup
[uredi | uredi kodo]- Podmnožica H grupe G je podgrupa za G, če in samo, če ni prazna in je zaprta za produkt in obratne vrednosti. Zaprtost pomeni naslednje: kadar sta a in b v H in sta v H tudi ab in a−1 tudi v H. Ta dva pogoja lahko kombiniramo v enakovredno trditev: kadar sta a in b v H, potem je tudi ab−1 je tudi v H. Kadar je H končen, je H podgrupa samo, če in samo če je H zaprt za zmnožek. V tem primeru vsak element iz H generira končno vrtilno grupo za H in obratna vrednost za a je enaka a−1 = an − 1, kjer n red za a.
- Zgornjo trditev lahko izrazimo s pomočjo homomorfizma. To pomeni, da je H podgrupa grupe G samo, če in samo, če je H podmnožica od G.
- Nevtralni element podgrupe je nevtralni element grupe. Kadar ima G nevtralni element eGin je H podgrupa za G z nevtralnim elementom eH, potem je eH = eG.
- Obratna vrednost elementa v podgrupi je obratna vrednost elementa v grupi. Kadar je H podgrupa grupe G in sta a in b elementa H tako, da je ab =ba = eH, potem je ab = ba =eG.
- Presek podgrup A in B je tudi podgrupa [1]. Unija podgrup A in B je podgrupa, če in samo če vsebujeta A ali B tudi drugega, ker sta primera 2 in 3 uniji 2Z in 3Z, njuna vsota 5 pa ni. Naslednji primer je unija x-osi in y-osi v ravnini. To služi kot primer dveh podgrup, katerih presek je natančno nevtralni element.
- Če je S podmnožica za G, potem obstoja najmanjša podgrupa, ki vsebuje S, ki jo najdemo tako, da vzamemo presek vseh podgrup, ki vsebujejo S. Označimo jo z <S> in zanjo pravimo, da je to podgrupa, ki jo generira S. Element iz G je v S je samo in samo, takrat ko je končni zmnožek elementov iz S, katerih presek je natančno nevtralni element.
- Vsak element grupe G generira ciklično podgrupo <a>. Kadar je <a> izomorfen za x Z/nZ za vsako pozitivno celo število, je n najmanjše pozitivno celo število za an = e in n se za a imenuje red . Kadar je <a> izomorfen za Z, pravimo, da ima a neskončni red.
- Podgrupe vsake dane grupe tvorijo popolno mrežo pod inkluzijo, ki jo imenujemo mreža podgrup. Kadar je nevtralni element za G, takrat je trivialna grupa {e} minimalna vrednost podgrupe za G. Pri tem pa je maksimalna vrednost sama po sebi že grupa.
Koseti in Lagrangeev izrek
[uredi | uredi kodo]Za dano podgrupo H in poljuben a v lahko definiramo levi koset aH = {ah :h v H}. Ker je preslikava obrnljiva H → aH in je dana z φ(h) = ah je to bijekcija. Vsak element v G se nahaja natančno v enem levem kosetu od H. Levi koset je enakovreden razred, ki odgovarja ekvivalenčni relaciji a1 ~ a2, če in samo, če je a1−1a2 v H. Število levih kosetov za H se imenuje indeks za H v G. Označujemo ga z [G : H].
Lagrangeev izrek trdi, da je za končne grupe v podgrupi:
kjer |G| in |H| označujeta red za G oziroma za H. Pti tem mora biti red vsake grupe za G ter red vsakega elementa od G delitelj za G.
Desni koseti so definirani podobno Ha = {ha : h v H}. To so tudi ekvivalenčni razredi za odgovarjajoče ekvivalenčne relacije. Njihovo število je enako [G : H].
Kadar je aH = Ha za vsak a v G, pravimo, da je H normalna podgrupa. Vsaka podgrupa z indeksom dva je normalna. Levi in desni koset je podgrupa in njegov komplement. Bolj splošno to povemo tako, da takrat, ko je p prvo praštevilo, ki deli red končne grupe G, potem je vsak indeks podgrupe, če ta obtoja, običajen.
Zgled za podgrupe Z8
[uredi | uredi kodo]Naj bo G ciklična grupa, ki ima elemente
in z grupno operacijo seštevanje po modulu osem. Pripadajoča Caleyjeva tabela je
| + | 0 | 2 | 4 | 6 | 1 | 3 | 5 | 7 |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 2 | 4 | 6 | 1 | 3 | 5 | 7 |
| 2 | 2 | 4 | 6 | 0 | 3 | 5 | 7 | 1 |
| 4 | 4 | 6 | 0 | 2 | 5 | 7 | 1 | 3 |
| 6 | 6 | 0 | 2 | 4 | 7 | 1 | 3 | 5 |
| 1 | 1 | 3 | 5 | 7 | 2 | 4 | 6 | 0 |
| 3 | 3 | 5 | 7 | 1 | 4 | 6 | 0 | 2 |
| 5 | 5 | 7 | 1 | 3 | 6 | 0 | 2 | 4 |
| 7 | 7 | 1 | 3 | 5 | 0 | 2 | 4 | 6 |
Ta grupa ima par netrivialnih podgrup J={0,4} in H={0,2,4,6}, kjer je J tudi podgrupa za H. Caylejeva tabela za H zgornji levi kvadrant Caylejeve tabele za G. Grupa G je ciklična. Takšne so tudi njene podgrupe. V splošnem so tudi podgrupe cikličnih grup tudi ciklične.
Zgled za podgrupe Z4
[uredi | uredi kodo]Vsaka grupa kot ima tudi toliko majhnih podgrup ter nevtralnih elementov na glavni diagonali:
Trivialna grupa ter grupa dveh elementov je Z2. Te majhne podgrupe niso navedene v spodnji tabeli.
 |
12 elementov
[uredi | uredi kodo]
Podgrupe:





8 elementov
[uredi | uredi kodo] Podgupe:    |
 Podgrupe: 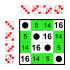  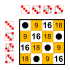 |
 Podgrupe: 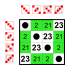  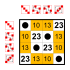 |
6 elementov
[uredi | uredi kodo] Podgrupe:  |
 Podgrupe:  |
 Podgrupe:  |
 Podgrupe:  |
4 elementi
[uredi | uredi kodo] |
 |
 |
 |
 |
 |
 |
3 elementi
[uredi | uredi kodo] |
 |
 |
 |
Glej tudi
[uredi | uredi kodo]Opombe in sklici
[uredi | uredi kodo]- ↑ Jacobson (2009), str. 41
Zunanje povezave
[uredi | uredi kodo]- Podgrupa na MathWorld (angleško)
- Kreiranje podgrupe (angleško)
- Podgrupe Arhivirano 2013-01-29 na Wayback Machine. (angleško)

![{\displaystyle [G:H]={|G| \over |H|}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e64b76d0605e6c7891273e65da28b5e431d4ea4)


