Prisekani oktaeder
| Prisekani oktaeder | |
|---|---|
 (animacija) | |
| vrsta | arhimedsko telo uniformni polieder |
| Elementi | F = 14, E = 36, V =24 (χ = 2) |
| stranske ploskve na stran | 6{4} + 8{6} |
| Conwayjev zapis | tO bT |
| Schläflijevi simboli | t{3,4} tr{3,3} ali |
| t0,1{3,4} ali t0,1,2{3,3} | |
| Wythoffov simbol | 2 4 | 3 3 3 2 | |
| Coxeter-Dinkinov diagram | |
| simetrija | Oh, B3, [4,3], (*432), red 48 Th, [3,3] in (*332), red 24 |
| vrtilna grupa | O, [4,3]+, (432), red 24 |
| diedrski kot | 4-6: cos(-1/√3) = 125º 15′ 51″ 6-6: cos(-1/3) = 109º 28′ 16″ |
| sklici | U08, C20, W7 |
| značilnosti | konveksen polpravilen zonoeder paraleloeder permutaeder |
 obarvane stranske ploskve |
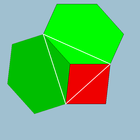 4.6.6 (slika oglišč) |
 tetrakisni heksaeder tetrakisni heksaeder (dualni polieder) |
 mreža telesa |
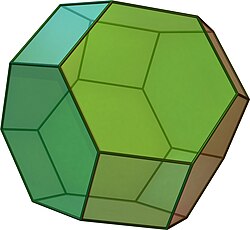
Prisekani oktaeder je v geometriji konveksni polieder. Je arhimedsko telo, eno od trinajstih konveksnih izogonalnih neprizmatičnih teles skonstruirano z dvema ali več vrstami pravilnih mnogokotniških stranskih ploskev.
Ima štirinajst pravilnih stranskih ploskev, od tega šest kvadratnih in osem šestkotniških, ter 36 robov in 24 oglišč. Vsaka izmed stranskih ploskev ima točkovno simetrijo in je tako prisekani oktaeder ali zonoeder.
Če ima prvotni prisekani oktaeder enotski rob (rob z dolžino 1), ima njegov dualni tetrakisni heksaeder rob z dolžino in .
Konstrukcija[uredi | uredi kodo]

|
|
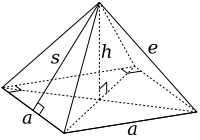
Prisekani oktaeder se lahko konstruira iz pravilnega oktaedra, ki ima dolžino stranice 3a, tako, da se odstrani šest kvadratnih piramid s pravimi koti, po eno za vsako oglišče. Te piramide imajo dolžino stranice a in stransko dolžino e pri a. Tako tvorijo enakostranične trikotnike. Ploščina osnovnice je a2. Ta oblika je podobna polovici oktaedra Johnsonovega telesa J1.
Iz značilnosti kvadratne piramide se lahko najde poševno višino s in višino piramide h:
Prostornina piramide je dana z V:
Ker se je odstranilo šest piramid, se s tem izgubi prostornino .
Kartezične koordinate in permutoeder[uredi | uredi kodo]
Vse permutacije vrednosti (0, ±1, ±2) so kartezične koordinate oglišč prisekanega oktaedra z dolžino roba a = √ 2, ki leži v izhodišču. Oglišča so tako vogali 12 pravokotnikov, ki imajo daljše robove vzporedne s koordinatnimi osmi.
Vektorji na robovih imajo kartezične koordinate (0, ±1,±1) in njihove permutacije. Pravokotnice na stranske ploskve za šest kvadratnih stranskih ploskev so (0,0, ±1), (0, ±1, 0) in (±1,0,0). Pravokotnice na stranske ploskve za 8 šestkotniških stranskih ploskev je (±1/ 3√3, ±1/ 3√3,±1/ 3√3). Skalarni produkt dveh normal na stranske ploskve je enak kosinusu diedrskega kota med sosednjima stranskima ploskvama. To pa je -1/3 ali -1/3√3 Diedrski kot je približno 1,910633 radianov (to je 109,471 °) za robove med dvema šestkotnikoma in 2,186276 radianov (to je 125,263 °)
Prisekani oktaeder se lahko prikaže tudi z mnogo bolj simetričnimi koordinatami v štirih razsežnostih. Vse permutacije vrednosti (1, 2, 3, 4) tvorijo oglišča prisekanega oktaedra v trirazsežnem prostoru x + y + z + w = 10. To pa pomeni, da je prisekani oktaeder permutoeder reda 4.
Površina in prostornina[uredi | uredi kodo]
Površina P in prostornina V prisekanega oktaedra z dolžino roba a sta:
Pravokotne projekcije[uredi | uredi kodo]
Prisekani oktaeder ima pet posebnih pravokotnih projekcij usrediščenih na oglišče, dve vrsti robov in dve vrsti stranskih ploskev (šestkotniki in kvadrati). Zadnji dve odgovarjata Coxeterjevima ravninama B2 in A2.
| usrediščeno na | oglišče | rob 4-6 |
rob 6-6 |
stransko ploskev – kvadrat |
stransko ploskev – šestkotnik |
|---|---|---|---|---|---|
| prisekani oktaeder |

|

|
|

|
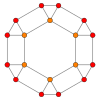
|
| projektivna simetrija |
[2] | [2] | [2] | [4] | [6] |
| tetrakisni heksaeder |

|
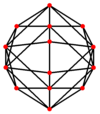
|

|
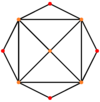
|

|
Uniformno barvanje[uredi | uredi kodo]
Obstajata dve uniformni barvanji, eno s tetraedrsko, drugo pa z oktaedrsko simetrijo:
| oktaedrska simetrija | tetraedrska simetrija (omniprisekani tetraeder) |
|---|---|
 barvanje 122 Wythoffov simbol: 2 4 | 3 |
 barvanje 123 Wythoffov simbol: 3 3 2 | |
Sorodni poliedri in tlakovanja[uredi | uredi kodo]
| {4,3} | t0,1{4,3} | t1{4,3} | t0,1{3,4} | {3,4} | t0,2{4,3} | t0,1,2{4,3} | {4,3} | h0{4,3} | h1,2{4,3} |
|---|---|---|---|---|---|---|---|---|---|

|

|

|

|
||||||
| {3,3} | t0,1{3,3} | t1{3,3} | t1,2{3,3} | t2{3,3} | t0,2{3,3} | t0,1,2{3,3} | s{3,3} |
|---|---|---|---|---|---|---|---|

|

|

|

|

| |||
| simetrija | sferna | ravninska | hiperbolična | |||||
|---|---|---|---|---|---|---|---|---|
| *232 [2,3] D3h |
*332 [3,3] Td |
*432 [4,3] Oh |
*532 [5,3] Ih |
*632 [6,3] P6m |
*732 [7,3] |
*832 [8,3] |
*∞32 [∞,3] | |
| red | 12 | 24 | 48 | 120 | ∞ | |||
| omniprisekana oblika |
 4.6.4 |
 4.6.6 |
 4.6.8 |
 4.6.10 |
 4.6.12 |
 4.6.14 |
 4.6.16 |
 4.6.∞ |
| Coxeter Schläfli |
t0,1,2{2,3} |
t0,1,2{3,3} |
t0,1,2{4,3} |
t0,1,2{5,3} |
t0,1,2{6,3} |
t0,1,2{7,3} |
t0,1,2{8,3} |
t0,1,2{∞,3} |
| omniprisekani duali |
 V4.6.4 |
 V4.6.6 |
 V4.6.8 |
 V4.6.10 |
 V4.6.12 |
 V4.6.14 |
V4.6.16 | V4.6.∞ |
| Coxeter | ||||||||
Ta polieder se lahko obravnava kot član uniformnih vzorcev s sliko oglišča (4.6.2p) in s Coxeter-Dinkinovim diagramom ![]()
![]()
![]()
![]()
![]() . Za p < 6 so člani zaporedja omniprisekani poliedri (zonoedri), ki so spodaj prikazani kot sferno tlakovanje. Za p > 6 je to tlakovanje hiperbolične ravnine, ki se prične s prisekano trojno sedemkotno tlakovanje.
. Za p < 6 so člani zaporedja omniprisekani poliedri (zonoedri), ki so spodaj prikazani kot sferno tlakovanje. Za p > 6 je to tlakovanje hiperbolične ravnine, ki se prične s prisekano trojno sedemkotno tlakovanje.
| simetrija | sferna | ravninska | hiperbolična... | |||||
|---|---|---|---|---|---|---|---|---|
| *232 [2,3] D3h |
*332 [3,3] Td |
*432 [4,3] Oh |
*532 [5,3] Ih |
*632 [6,3] P6m |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] | |
| red | 12 | 24 | 48 | 120 | ∞ | |||
| prisekane oblike |
 2.6.6 |
 3.6.6 |
 4.6.6 |
 5.6.6 |
 6.6.6 |
 7.6.6 |
 8.6.6 |
 3.4.∞.4 |
| Coxeter Schläfli |
t0,1{3,2} |
t0,1{3,3} |
t0,1{3,4} |
t0,1{3,5} |
t0,1{3,6} |
t0,1{3,7} |
t0,1{3,8} |
t0,1{3,∞} |
| N-kisne oblike |
 V2.6.6 |
 V3.6.6 |
 V4.6.6 |
 V5.6.6 |
 V6.6.6 |
 V7.6.6 | ||
| Coxeter | ||||||||
Tlakovanja[uredi | uredi kodo]
Prisekani oktaeder obstaja v treh različnih oblikah konveksnih uniformnih satovij (v tlakovanjih, ki zapolnjujejo prostor).
Celično prehodno dvojno prisekano kubično satovje se lahko gleda tudi kot Voronojevo tlakovanje telesno centrirane kubične mreže. Prisekani oktaeder je eden izmed petih trirazsežnih osnovnih paraleloedrov
| dvojno prisekana kubična | kantiprisekana kubična | prisekana alternirana kubična. |
|---|---|---|
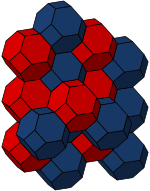
|

|

|
Glej tudi[uredi | uredi kodo]
Zunanje povezave[uredi | uredi kodo]
- Weisstein, Eric Wolfgang. »Truncated Octahedron«. MathWorld.
- Weisstein, Eric Wolfgang. »Permutohedron«. MathWorld.
- Trirazsežni konveksni uniformni poliedri (angleško)
- Mreža prisekanega oktaedra (angleško)











