Vrtnica (matematika)

Krivulja vrtnica s 7 listi (k = 7)

Krivulja vrtnica z 8 listi (k=4).

Vrtnice, ki so določene z $r=\sin k \theta$, za različne vrednosti k=n/d.

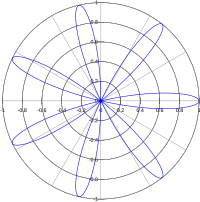
Vrtnica (tudi rodoneja) je družina krivulj, ki so sinusoide narisane v polarnih koordinatah. Krivulje so si podobne, lahko jih podamo s pomočjo enačbe

$\!\,r=\cos(k\theta).$

kjer je $k \,$ celo število, ki določa obliko oziroma število listov, ki jih ima vrtnica, na naslednji način:

• $2k \,$ listov kadar je $k \,$ paren
• $k \,$ listov kadar je $k \,$ neparen.

Ime rodoneja je krivulji dal rimskokatoliški duhovnik, filozof, matematik in inženir Luigi Guido Grandi (1671 – 1742) med leti 1723 in 1728 .

Lastnosti

• Kadar se $k \,$ konča z 0,5 (primeri 0,5, 2,5, ….) ima krivulja 4 liste.
• Kadar se $k \,$ konča z 1/3 ali 5/6 in je večji od 1 (primeri: 1,6666667, 2, 8,333333, …..) ima krivulja 12k listov
• Kadar se $k \,$ konča z 1/3 in je večji od 1 (primeri: 1,33334, 2,333334, ….) ima krivulja obliko vrtnice ter
  • ima 3k listov, če je $k \,$ paren
  • ima 6k listov, če je $k \,$ neparen
• Kadar se $k \,$ konča z 2/3 in je večji od 1 (primeri: 1,6666667, 2,66666667, …..) ima ima krivulja obliko vrtnice ter
  • ima 6k listov, če je $k \,$ paren
  • ima 3k listov, če je $k \,$ neparen

• Kadar je $k \,$ racionalno število je krivulja zaprta in ima končno dolžino.
• kadar pa je $k \,$ iracionalno število, je krivulja zaprta in ima neskončno dolžino.
• Kadar je $k \,$ paren, se bo krivulja izrisala točno enkrat, med tem, ko se bo $\theta \,$ povečal od 0 do $2\pi \,$.

Ploščina

Če ima krivulja enačbo

$r=a \cos (k\theta)\,$

kjer je

• $k \,$ pozitivno celo število, je za paren $k \,$

ploščina enaka

$\frac{1}{2}\int_{0}^{2\pi}(a\cos (k\theta))^2\,d\theta = \frac {a^2}{2} \left(\pi + \frac{\sin(4k\pi)}{4k}\right) = \frac{\pi a^2}{2}$

in je za neparen $k \,$ enaka

$\frac{1}{2}\int_{0}^{\pi}(a\cos (k\theta))^2\,d\theta = \frac {a^2}{2} \left(\frac{\pi}{2} + \frac{\sin(2k\pi)}{4k}\right) = \frac{\pi a^2}{4}$.

To velja tudi za vrtnice, ki so določene z enačbo

$r=a \sin (k\theta)\,$.

Glej tudi

• Lissajousova krivulja
• štiriperesna deteljica
• Maurerjeva vrtnica

Zunanje povezave

• Vrtnica na MathWorld (v angleščini)
• Vrtnica na Xah Lee Web (v angleščini)
• Vrtnica v Encyclopedia of Science (v angleščini)
• Aplet za kreiranje vrtnice (v angleščini)