Agnesin koder

Krivulje Agnesini kodri s parametri a = 1, a = 2, a = 4, in a = 8

Krivulja Agnesin koder (njen nastanek).

Agnesin koder (tudi versarija) je ravninska krivulja tretjega reda, ki je simetrična glede na os y in se asimptotsko približuje osi x.

Krivuljo je proučevala italijanska matematičarka, filozofinja in jezikoslovka Maria Gaetana Agnesi (1718–1799). Proučevala sta jo še francoski pravnik, matematik in fizik Pierre de Fermat (1601–1665) in italijanski rimskokatoliški duhovnik, filozof, matematik in inženir Luigi Guido Grandi (1671–1742).

Krivulja se asimptotično približuje tangenti na krožnico skozi izhodišče (točka O).

Nastanek

Animacija, ki prikazuje nastanek Agnesinega kodra.

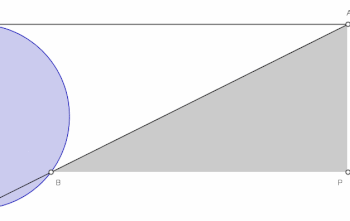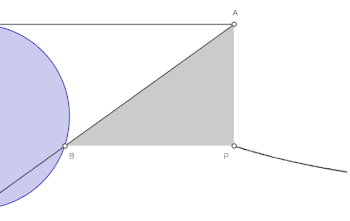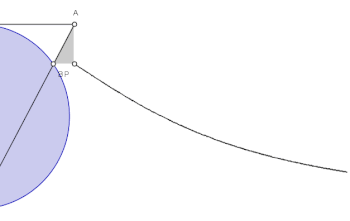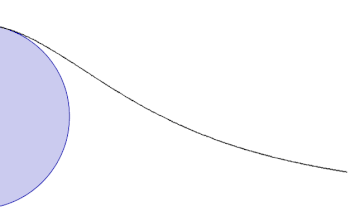
Izberimo stalno točko $O \,$ na krožnici. Nato za za poljubno točko $A \,$ na krožnici narišimo sekanto OA. Točka $M \,$ je nasproti točke $O \,$. Premica OM skozi N in premica, ki je pravokotna na OM skozi A, se sekata v točki P (glej risbo).

Enačba Agnesinega kodra v kartezičnih koordinatah

V kartezičnem koordinatnem sistemu je enačba

$\!y = \frac{8a^3}{x^2+4a^2}$.

kjer je

• $a \,$ polmer krožnice

Če je $a = 1/2 \,$, dobimo enostavnejšo enačbo

$\!y = \frac{1}{x^2+1}.$

Parametrična oblika enačbe Agnesinega kodra

V parametrični obliki je enačba Agnesinega kodra

$\!x = 2a \tan \theta,\ y = 2a \cos ^2 \theta \,$.

kjer je

• $\theta$ kot med OM in OA (glej zgoraj)

Če pa je $\theta$ kot med točkama O in A ter x-osjo (merjeno v nasprotni smeri od gibanja kazalcev na uri), potem dobimo drugo parametrično obliko enačbe Agnesinega kodra

$\!x = 2a \cot \theta,\ y=2a\sin ^2 \theta.\,$

Značilnosti

• ploščina med Agnesinim kodrom in njeno asimptoto je $4 \pi a^2$
• težišče krivulje je v točki $(0, a)$

Glej tudi

• Cauchyjeva porazdelitev
• Lorentzova funkcija
• seznam krivulj

Zunanje povezave

• Agnesin koder na MathWorld (v angleščini)
• Agnesin koder v Encyclopédie des Formes Mathématiques Remarquable (v francoščini)
• Agnesin koder na MacTutor (v angleščini)
• Agnesin koder na ProofWiki (v angleščini)