Evdoksova kampila

Slika Evdoksove kampile.

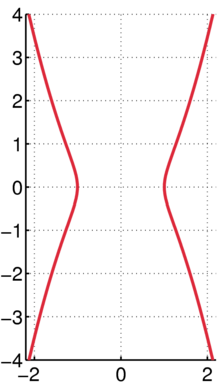
Evdoksova kampila je kvartna (četrte stopnje) krivulja, ki ima v kartezičnem koordinatnem sistemu enačbo:

$x^4=x^2+y^2 \!\, ,$

(pri tem ne upoštevamo rešitve x = y = 0).

V polarnem koordinatnem sistemu pa je njena enačba:

$r= \sec^2\theta \!\, .$

Krivuljo je proučeval že starogrški astronom, matematik, zdravnik in filozof Evdoks (410 pr. n. št. – 347 pr. n. št.) v povezavi s podvojitvijo kocke.

Evdoksova kampila je simetrična glede na os-y in os-x. Krivulja seka x-os v točkah (-1, 0) in (1, 0). Ima točke prevoja v:

$(\pm\sqrt{3/2},\pm\sqrt{3}/2)$ (štiri točke).

Zgornja polovica je asimptotična na krivuljo:

$x^2-\frac12$ kadar velja $x \to \infty \!\, .$

To lahko zapišemo kot:

$y = x^2\sqrt{1-x^{-2}} = x^2 - \frac12 \sum_{n \ge 0} C_n(2x)^{-2n} \!\, ,$

kjer je:

$C_n = \frac1{n+1} \binom{2n}{n} \!\,$

in $n$ n-to Catalanovo število.

Zunanje povezave

• Evdoksova kampila na MathWorld (v angleščini)