Parabola

Iz Wikipedije, proste enciklopedije

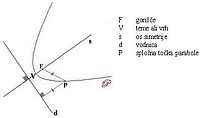
Parábola je geometrijsko mesto točk ravnine, ki so od dane premice (vodnica parabole) enako oddaljene kot od dane točke (gorišča parabole).

V primeru, ko ima vodnica enačbo , in je gorišče točka , zadošča parabola enačbi:

Vse ostale parabole dobimo z vzporednimi premiki in vrtenjem te parabole.

[uredi] Parabola kot graf kvadratne funkcije

Parabola, ki ima v kartezičnem koordinatnem sistemu simetralo vzporedno osi y, je graf kvadratne funkcije, določena z enačbo:

kjer so realna števila , b in c koeficienti parabole.

Vodilni koeficient a »nadzira« konkavnost ali konveksnost parabole:

• a > 0 : parabola je konveksna in teme parabole ima najmanjšo možno ordinato,
• a < 0 : parabola je konkavna in teme parabole ima največjo možno ordinato.

Linearni koeficient b je vezan na os simetrije parabole. Os je premica vzporedna ordinatni osi in gre skozi točko z absciso -b/2a.

Svobodni ali prosti koeficient c nam da presek parabole z ordinatno osjo.

[uredi] Zunanje povezave

p • p • u Ravninske krivulje 1. reda premica Stožnice (2. reda) elipsa • krožnica • hiperbola • parabola Lemniskate Bernoullijeva • Boothova • Cassinijeva jajčnica • Descartesov oval • Geronova • hipopeda • polinomska Spirale arhimedske • (Arhimedova • (parabolična • (Fermatova)) • hiperbolična • kvadratna hiperbolična • lituus) • enakokotna • evolventa krožnice • klotoida • logaritemska • sinusoidna • zlata Fraktalne Hilbertova • Kochova snežinka • Lévyjeva krivulja C • krivulja Minkowskega • Peanova Nastale s kotaljenjem po drugi krivulji cikloida • (brahistokrona) • epitrohoida • (Pascalov polž) • epicikloida • evoluta • evolventa • (evolventa krožnice) • hipocikloida • (astroida • deltoida) • hipotrohoida • trohoida • (nefroida • (Freethova nefroida) • srčnica) 3. reda Agnesin koder • cisoida • (Dioklesova cisoida) • Descartesov list • kubična elipsa • kubična hiperbola • kubična parabola • kubična parabolična hiperbola • Maclaurinova trisektrisa • Neilova parabola • okljuk (Newtonova serpentina) • strofoida 4. reda Evdoksova kampila • hudičeva • konhoida • (Nikomedova konhoida • Pascalov polž) • Tschirnhausova kubična • deteljica • (dvoperesna • enoperesna • triperesna) Druge Bézierova • kvadratrika • (Hipijeva kvadratika) • kohleoida • Lissajouseva • oval • radiodroma • (traktrisa) • ribja • s konstantno širino • sinusoida • superelipsa • Talbotova • trisektrisa (polžasta trisektrisa • Cevova trisektrisa • Maclaurinova trisektrisa) • vrtnica • (štiriperesna deteljica) • verižnica • Wattova