Kvadratni koren števila 3

Seznam števil Iracionalna števila γ ζ(3) ρ √2 Φ √3 √5 δS e π δ
dvojiško	1,10111011011001111010...
desetiško	1,7320508075688772935...
šestnajstiško	1,BB67AE8584CAA73B...
šestdesetiško	1; 43, 55, 22, 58, 27, 57, 56, ...
verižni ulomek	$[1;{\overline {1,2}}]\,$ Verižni ulomek ${\sqrt {3}}\!\,$ je periodičen.

Kvadratni koren števila 3 je pozitivno realno število, ki pomnoženo samo s seboj da naravno število 3. Točneje se imenuje glavni kvadratni koren števila 3, da se ga ločuje od negativnega števila z enako značilnostjo. Označuje se v obliki surda:

${\sqrt {3}}\!\,$    ali    √3,

lahko pa se ga zapiše tudi s potenčnim zapisom kot:

$3^{1/2}\!\,$    ali    3^1/2, oziroma z zapisom Unicode 3^½.

Njegova vrednost na 65 desetiških mest je (OEIS A002194):

1,73205080756887729352744634150587236694280525381038062805580697945...

Do sedaj so izračunali vsaj deset milijard števk (10×10⁹). Zaokrožena vrednost 1,732 je točna z napako manjšo od 0,01 % dejanske vrednosti. Dober približek z ulomkom je:

${\sqrt {3}}\approx {\frac {97}{56}}=1,732{\overline {142857}}\!\,$

s periodo dolžine 6.

Ni znano ali je $\scriptstyle {\sqrt {3}}\,$ normalno število.

Zgodovina

Baudhajana je včasih za $\scriptstyle {\sqrt {3}}\,$ uporabljal peti racionalni približek ${\tfrac {26}{15}}\,$. Poznal je tudi enajsti racionalni približek:

${\sqrt {3}}\approx 1+{\frac {2}{3}}+{\frac {1}{3\cdot 5}}-{\frac {1}{3\cdot 5\cdot 52}}={\frac {1351}{780}}=1,73{\overline {205128}}\!\,.$

Arhimed je v delu Merjenje kroga navedel vrednost:

${\frac {265}{153}}<{\sqrt {3}}<{\frac {1351}{780}}\!\,,$

točno na ${\tfrac {2}{23409}}\,$ (4 desetiška mesta) in ${\tfrac {1}{608400}}\,$ (6 desetiških mest). Pri tem ni navedel točnega postopka, verjetno pa je uporabil iteracijo, neko vrsto intepolacijske metode ali kombinacijo več metod. Na ta način je sicer najboljša spodnja meja enaka:

${\frac {989}{571}}<{\sqrt {3}}\!\,,$

ni pa jasno zakaj je Arhimed ni navedel. Mogoče je potreboval boljšo zgornjo mejo in je računal naprej, spodnje meje pa ni navajal. Čeprav svojih metod ni pojasnil, se lahko približka dobita na enak način kot rešitev Pellove enačbe za n = 3:

$x^{2}-3y^{2}=1\!\,.$

To je vodilo do razprav koliko te teorije števil je bilo dostopno Arhimedu. Razprava gre vsaj do de Lagnyja leta 1723, obravnaval pa jo je bolj eksplicitno Zeuthen. Hultsch (1833–1906) in Hunrath (rojen 1847) sta poudarila, da se meji lahko izračunata hitro s preprostima binomskima mejama na kvadratnih korenih, kar je sorodno metodi s popolnim kvadratom v Evklidovih Elementih (2.4, 7). To metodo je zagovarjal Heath. Čeprav je omenjena samo ena pot do mej, sta v bistvu še dve drugi in meje so neodvisne od metode. Meji se lahko izračunata tudi z iterativno geometrijsko konstrukcijo, ki jo je predlagal Arhimed v delu Ostomahion pri računanju pravilnega dvanajstkotnika. V tem primeru je naloga poiskati racionalne približke funkcije tangensa π/12.

Kvadratni koren števila 3 je iracionalno algebrsko število. Znano je tudi kot Teodorova konstanta, imenovana po Teodoru Kirenskem. Teodor je dokazal, da so kvadratni koreni števil od 3 do 17 brez popolnih kvadratov 4, 9 in 16 iracionalna števila.

Dokazi iracionalnosti

Dokaz z neskončnim spustom

Dokaz iracionalnosti kvadratnega korena števila 3 vsebuje Fermatovo metodo neskočnega spusta:

Predpostavi se, da je $\scriptstyle {\sqrt {3}}\,$ racionalno število in se ga izrazi s pokrajšanimi členi (kot popolnoma okrajšani ulomek) ${\tfrac {m}{n}}\,$ za naravni števili m in n.

Če se ulomek pomnoži z 1, bo vrednost ostala nespremenjena:

${\frac {m({\sqrt {3}}-q)}{n({\sqrt {3}}-q)}}\!\,,$

kjer je q največje celo število manjše od $\scriptstyle {\sqrt {3}}\,$. Pri tem sta števec in imenovalec pomnožena s številom manjšim od 1.

Z množenjem je:

${\frac {m{\sqrt {3}}-mq}{n{\sqrt {3}}-nq}}\!\,.$

Od tod sledi, da se m lahko zamenja z $n\scriptstyle {\sqrt {3}}\,$:

${\frac {n{\sqrt {3}}^{2}-mq}{n{\sqrt {3}}-nq}}\!\,.$

Tako se lahko tudi $\scriptstyle {\sqrt {3}}\,$ zamenja z ${\tfrac {m}{n}}\,$ v imenovalcu:

${\frac {n{\sqrt {3}}^{2}-mq}{n{\frac {m}{n}}-nq}}\!\,.$

Kvadrat $\scriptstyle {\sqrt {3}}\,$ je enak 3. Ker je ${\tfrac {m}{n}}\,$ pomnoženo z n, je njun produkt enak m:

${\frac {3n-mq}{m-nq}}\!\,.$

Tako se lahko $\scriptstyle {\sqrt {3}}\,$ izrazi z nižjimi členi od ${\tfrac {m}{n}}\,$ (ker je prvi korak zmanjšal velikost števca in imenovalca, naslednji koraki pa ju niso spremenili) kot ${\tfrac {3n-mq}{m-nq}}\,$, kar je protislovje domnevi, da je imel ${\tfrac {m}{n}}\,$ najmanjše člene.

Dokaz s protislovjem

Pri drugem dokazu se predpostavi, da je ${\sqrt {3}}={\tfrac {m}{n}}\,$, kjer je ${\tfrac {m}{n}}\,$ popolnoma okrajšani ulomek:

Če se oba člena pomnožita z n in nato kvadrirata, je:

$3n^{2}=m^{2}\!\,.$

Ker je leva stran deljiva s 3, je deljiva tudi desna, kar zahteva, da je m deljiv s 3. Zato se lahko m izrazi kot mnogokratnik 3k:

$3n^{2}=(3k)^{2}=9k^{2}\!\,.$

Če se oba člena deli s 3, se tako dobi:

$n^{2}=3k^{2}\!\,.$

Ker je desna stran deljiva s 3, je tudi leva, in zato tudi n. Ker sta n in m oba deljiva s 3, imata skupni faktor, in ${\tfrac {m}{n}}\,$ ni popolnoma okrajšani ulomek, kar nasprotuje izvirni premisi.

Značilnosti

Geometrija in trigonometrija

Enakostranični trikotnik z dolžino stranice 2 ima dolžino višine enako $\scriptstyle {\sqrt {3}}\,$.

$\scriptstyle {\sqrt {3}}\,$ je enak dolžini med vzporednima stranicama pravilnega šestkotnika z dolžino stranice 1, oziroma dvakratniku dolžine apoteme.

$\scriptstyle {\sqrt {3}}\,$ je enak dolžini telesne diagonale enotske kocke.

$\scriptstyle {\sqrt {3}}\,$ je enak površini tetraedra z robom dolžine 1

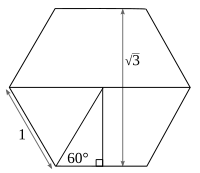
Kvadratni koren števila 3 je enak dolžini stranice enakostraničnega trikotnika z očrtano krožnico s premerom 1.

Če se enakostranični trikotnik s stranicami dolžine 1 razdeli na dve enaki polovici z razpolovitvijo notranjega kota, kjer imata nastala pravokotna trikotnika hipotenuzi enaki 1, kateti pa imata dolžini ${\tfrac {1}{2}}\,$ in ${\tfrac {\scriptstyle {\sqrt {3}}}{2}}\,$. Tako je trigonometrična funkcija tangens 60° enaka $\scriptstyle {\sqrt {3}}\,$, sinus 60° in kosinus 30° pa sta oba enaka ${\tfrac {\scriptstyle {\sqrt {3}}}{2}}\,$.

$\scriptstyle {\sqrt {3}}\,$ je enako razdalji med vzporednima stranicama pravilnega šestkotnika z dolžino stranice 1, oziroma dvakratniku dolžine apoteme. V kompleksni ravnini se to izrazi kot $\scriptstyle i{\sqrt {3}}\,$.

$\scriptstyle {\sqrt {3}}\,$ je enako dolžini telesne diagonale enotske kocke.

$\scriptstyle {\sqrt {3}}\,$ je enako površini tetraedra z robom dolžine 1.

Kvadratni koren števila 3 se pojavlja tudi v algebrskih izrazih za različne točne trigonometrične konstante: sinusi 3°, 12°, 15°, 21°, 24°, 33°, 39°, 48°, 51°, 57°, 66°, 69°, 75°, 78°, 84° in 87°.

Obratna vrednost

Diara (vesica piscis) ima razmerje med veliko in manjšo osjo enako obratni vrednosti $\scriptstyle {\sqrt {3}}\,$ (OEIS A020760):

${\frac {1}{\sqrt {3}}}=0,5773502691896257645091487805019574556476017512701268760186023264\ldots \!\,,$

kar se lahko pokaže s konstrukcijo dveh enakostraničnih trikotnikov znotraj lika.

Drugo

Velja naslednja zveza:

${\sqrt {3}}={\frac {\Gamma (1/6)\Gamma (5/6)}{\Gamma (1/3)\Gamma (2/3)}}\!\,,$

kjer je $\Gamma \,$ funkcija Γ.

Verižni ulomek

Število $\scriptstyle {\sqrt {3}}\,$ je kvadratno iracionalno število in je zato njegov razvoj v neskončni verižni ulomek periodičen (OEIS A040001):

${\begin{aligned}{\sqrt {3}}&=1+{\cfrac {1}{1+{\cfrac {1}{2+{\cfrac {1}{1+{\cfrac {1}{2+{\cfrac {1}{1+\ddots }}}}}}}}}}\equiv [1;1,2,1,2,1,2,1,\ldots ]\equiv [1;{\overline {1,2}}]\\&=\left\{{\color {red}{1}},{\color {red}{2}},{\frac {3}{2}},{\color {red}{\frac {5}{3}}},{\color {red}{\frac {7}{4}}},{\frac {12}{7}},{\color {red}{\frac {19}{11}}},{\color {red}{\frac {26}{15}}},{\frac {45}{26}},{\color {red}{\frac {71}{41}}},{\color {red}{\frac {97}{56}}},{\frac {168}{97}},{\color {red}{\frac {265}{153}}},{\color {red}{\frac {362}{209}}},{\frac {627}{362}},{\color {red}{\frac {989}{571}}},{\color {red}{\frac {1351}{780}}},{\frac {2340}{1351}},{\color {red}{\frac {3691}{2131}}},{\color {red}{\frac {5042}{2911}}},\right.\\&\left.\qquad {\frac {8733}{5042}},{\color {red}{\frac {13775}{7953}}},\ldots \right\}\,\!.\end{aligned}}$

Konvergenti verižnega ulomka so označeni z rdečo, njihovi števci so: 1, 2, 5, 7, 19, 26, 71, 97, ... (OEIS A002531), imenovalci pa: 1, 1, 3, 4, 11, 15, 41, 56, ... (OEIS A002530). Drugi členi, označeni s črno, so polkonvergenti. Vrednost vsakega prvega polkonvergenta mora biti boljša od vrednosti predhodnega konvergenta. V primeru verižnega ulomka za $\scriptstyle {\sqrt {3}}\,$ so vse vrednosti boljše in tako so vsi polkonvergenti ustrezni.

Lahko se ga izrazi tudi s posplošenimi verižnimi ulomki, kot je na primer:

$[2;-4,-4,-4,...]=2-{\cfrac {1}{4-{\cfrac {1}{4-{\cfrac {1}{4-\ddots }}}}}}\!\,,$

kar je [1; 1, 2, 1, 2, 1, 2, 1, ...] izračunano za vsak drugi člen.

Kvadratni koren števila −3

Množenje $\scriptstyle {\sqrt {3}}\,$ z imaginarno enoto da kvadratni koren števila −3, imaginarno število. Točneje:

${\sqrt {-3}}=\pm {\sqrt {3}}i\!\,.$

Je Eisensteinovo celo število. Izraženo je kot razlika med nerealnimi kubičnimi koreni iz 1, (ki so Eisensteinova cela števila).

Računanje

Konvergenčna metoda

Za računanje $\scriptstyle {\sqrt {3}}\,$ obstaja več metod. Ena od njih uporablja rekurzivno zaporedje in da vse delne količnike neskončnega verižnega ulomka:

$a_{1}=\lfloor {\sqrt {k}}\rfloor ,\qquad a_{n+1}={\frac {a_{n}+k}{a_{n}+1}},\quad (n=1,2,3,\ldots )\!\,,$

kjer je $\lfloor {\sqrt {k}}\rfloor \,$ celi del števila $k\,$. Za $k=3\,$ so prvi približki:

$a_{1}=\lfloor {\sqrt {3}}\rfloor =1\!\,,$

$a_{2}={\frac {a_{1}+3}{a_{1}+1}}=2\!\,,$

$a_{3}={\frac {a_{2}+3}{a_{2}+1}}={\frac {5}{3}}=1,{\overline {6}}\!\,,$

$a_{4}={\frac {a_{3}+3}{a_{3}+1}}={\frac {7}{4}}=1,75\!\,,$

$a_{5}={\frac {a_{4}+3}{a_{4}+1}}={\frac {19}{11}}=1,{\overline {72}}\!\,,$

$a_{6}={\frac {a_{5}+3}{a_{5}+1}}={\frac {26}{15}}=1,7{\overline {3}}\!\,,$

$a_{7}={\frac {a_{6}+3}{a_{6}+1}}={\frac {71}{41}}=1,{\overline {73170}}\!\,,$

$a_{8}={\frac {a_{7}+3}{a_{7}+1}}={\frac {97}{56}}=1,732{\overline {142857}}\!\,,$

$a_{9}={\frac {a_{8}+3}{a_{8}+1}}={\frac {265}{153}}=1,{\overline {7320261437908496}}\!\,,$

$a_{10}={\frac {a_{9}+3}{a_{9}+1}}={\frac {362}{209}}=1,{\overline {732057416267942583}}\!\,,$

${\begin{aligned}a_{11}&={\frac {a_{10}+3}{a_{10}+1}}={\frac {989}{571}}\\&=1,{\overline {732049036777583187390542907180\ldots }}\!\,,\end{aligned}}$

...

Približki z lihimi indeksi strogo naraščajo in so manjši od $\scriptstyle {\sqrt {3}}\,$, približki s sodimi indeksi pa strogo padajo in so večji od $\scriptstyle {\sqrt {3}}\,$.

Babilonska metoda

V drugi rekurzivni metodi, ki uporablja aritmetično sredino, približki konvergirajo kvadratično in zaporedje je monotono padajoče. n-ti člen je enak 2^n-1-temu konvergentu neskončnega verižnega ulomka. Metodo pripisujejo Heronu, znana pa je bila verjetno že Babiloncem:

$a_{1}=\lfloor {\sqrt {k}}\rfloor ,\qquad a_{n+1}={\frac {1}{2}}\left(a_{n}+{\frac {k}{a_{n}}}\right),\qquad (n=1,2,3,\ldots )\!\,,$

$a_{1}=\lfloor {\sqrt {3}}\rfloor =1\!\,,$

$a_{2}={\frac {1}{2}}\left(a_{1}+{\frac {3}{a_{1}}}\right)=2\!\,,$

$a_{3}={\frac {1}{2}}\left(a_{2}+{\frac {3}{a_{2}}}\right)={\frac {7}{4}}=1,75\!\,,$

$a_{4}={\frac {1}{2}}\left(a_{3}+{\frac {3}{a_{3}}}\right)={\frac {97}{56}}=1,732{\overline {142857}}\!\,,$

${\begin{aligned}a_{5}&={\frac {1}{2}}\left(a_{4}+{\frac {3}{a_{4}}}\right)={\frac {18817}{10864}}\\&=1,7320{\overline {50810014727540500736377025\ldots }}\!\,,\end{aligned}}$

${\begin{aligned}a_{6}&={\frac {1}{2}}\left(a_{5}+{\frac {3}{a_{5}}}\right)={\frac {708158977}{408855776}}\\&=1,73205{\overline {0807568877295254353946072\ldots }}\!\,,\end{aligned}}$

...

Prvi člen je lahko tudi drug, ki je bližje iskanemu številu, na primer naslednji lihi približek iz prve metode ${\tfrac {5}{3}}\,$, kar da:

$a_{1}={\frac {5}{3}}=1,{\overline {6}}\!\,,$

$a_{2}={\frac {1}{2}}\left(a_{1}+{\frac {3}{a_{1}}}\right)={\frac {26}{15}}=1,7{\overline {3}}\!\,,$

$a_{3}={\frac {1}{2}}\left(a_{2}+{\frac {3}{a_{2}}}\right)={\frac {1351}{780}}=1,73{\overline {205128}}\!\,,$

${\begin{aligned}a_{4}&={\frac {1}{2}}\left(a_{3}+{\frac {3}{a_{3}}}\right)={\frac {3650401}{2107560}}\\&=1,732{\overline {050807568942283968190703941\ldots }}\!\,,\end{aligned}}$

${\begin{aligned}a_{5}&={\frac {1}{2}}\left(a_{4}+{\frac {3}{a_{4}}}\right)={\frac {26650854921601}{15386878263120}}\\&=1,7320{\overline {50807568877293527446342725\ldots }}\!\,,\end{aligned}}$

...

Druge uporabe

Elektroenergetika

V elektroenergetiki je električna napetost med dvema fazama v trifaznem toku enaka $\scriptstyle {\sqrt {3}}\,$ krat voda nevtralne napetosti. To je zato ker sta poljubni dve fazi razmaknjeni za kot 120°. Dve točki na krožnici pod kotom 120° sta oddaljeni med seboj za dolžino $\scriptstyle {\sqrt {3}}\,$ krat polmer krožnice.

Glej tudi

• kvadratni koren števila 2
• kvadratni koren števila 5
• dinamični pravokotnik

Viri

• Brown, Kevin (2015), Archimedes and the Square Root of 3 (v angleščini), pridobljeno 16. februarja 2016
• Davies, E. B. (3. januar 2011), Archimedes' calculations of square roots (PDF) (v angleščini)
• Drnovšek, Roman (1996), »Računanje kvadratnega korena iz naravnega števila« (PDF), Presek, 24 (6): 372–375
• Grant, Mike; Perella, Malcolm (Julij 1999), »Descending to the irrational«, Mathematical Gazette, 83 (497): 263–267, doi:10.2307/3619054
• Heath, Thomas Little (1897), The Works of Archimedes, Cambridge University: University Press, pridobljeno 30. junija 2008
• Knorr, Wilbur Richard (1976), »Archimedes and the measurement of the circle: a new interpretation«, Archive for History of Exact Sciences, 15 (2): 115–140, doi:10.1007/bf00348496, JSTOR 41133444, MR 0497462
• McKeeman, Bill (23. november 2010), »The Computation of Pi by Archimedes«, Matlab Central (v angleščini), pridobljeno 30. oktobra 2012
• Lokar, Matija (1987), »Računanje kvadratnega korena« (PDF), Presek, 15 (6): 322–325
• S., D.; Jones, M. F. (1968), »22900D approximations to the square roots of the primes less than 100«, Mathematics of Computation, 22 (101): 234–235, doi:10.2307/2004806, JSTOR 2004806
• Uhler, Horace Scudder (1951), »Approximations exceeding 1300 decimals for √3, ⁠1/√3⁠, sin(⁠π/3⁠) and distribution of digits in them«, Proc. Nat. Acad. Sci. U. S. A., 37 (7): 443–447, PMC 1063398, PMID 16578382 {{citation}}: templatestyles stripmarker v |title= na mestu 48 (pomoč)
• Wells, David (1997), The Penguin Dictionary of Curious and Interesting Numbers (popravljena izd.), London: Penguin Group, str. 23
• Whitford, Edward Everett (1912), The Pell equation, doktorska disertacija, Univerza Columbia
• Wiseman, Julian D. A. (Junij 2008), Sin and Cos in Surds (v angleščini)

Zunanje povezave

• Weisstein, Eric Wolfgang. »Theodorus' Constant«. MathWorld.