Algebrska geometrija

Ta Togliattijeva ploskev je vozliščna algebrska ploskev pete stopnje. Slika prikazuje del njenega realnega geometrijskega mesta točk.

Algébrska geometríja je veja matematike, ki klasično raziskuje ničle polinomov z več spremeljivkami. Moderna algebrska geometrija temelji na rabi tehnik abstraktne algebre, največ iz komutativne algebre, za reševanje geometrijskih problemov o teh množicah ničel.

Temeljni predmeti proučevanja algebrske geometrije so algebrske varietete, ki so geometrijske manifestacije rešitev sistemov polinomskih enačb. Zgledi najbolj raziskanih razredov algebrskih varietet so: ravninske algebrske krivulje, ki vključujejo premice, stožnice (krožnice, parabole, elipse, hiperbole), kubične krivulje, kot na primer eliptične krivulje, in kvartične krivulje, kot so Bernoullijeve lemniskate in Cassinijevi ovali. Točka na ravnini pripada algebrski krivulji, če njene koordinate zadoščajo dani polinomski enačbi. Osnovna vprašanja vključujejo raziskovanje točk posebnega pomena, kot so singularne točke, prevojne točke in točke v neskončnosti. Naprednejša vprašanja vključujejo topologijo krivulje in razmerja med krivuljami, podanimi z različnimi enačbami.

Algebrska geometrija zavzema osrednje mesto v moderni matematiki in ima številne konceptualne povezave s tako različnimi področji, kot so kompleksna analiza, topologija in teorija števil. Sprva kot študij sistemov polinomskih enačb več spremenljivk, se predmet algebrske geometrije začne tam, kjer se konča reševanje enačb, in postane še pomembnejši kot razumevanje vrojenih značilnosti celote rešitev sistema enačb kot najti specifično rešitev – to vodi v nekatera najgloblja področja v vsej matematiki, tako konceptualno kot v smislu tehnike.

V 20. stoletju se je algebrska geometrija razcepila na več podpodročij:

• glavni tok algebrske geometrije je posvečen študiju kompleksnih točk algebrskih varietet in na splošno točkam s koordinatami v algebrsko zaprtem polju.
• realna algebrska geometrija je raziskovanje realnih točk algebrskih varietet.
• diofantska geometrija in splošneje aritmetična geometrija je raziskovanje točk algebrske varietete s koordinatami v poljih, ki niso algebrsko zaprti, in se pojavljajo v algebrski teoriji števil, kot so polja racionalnih števil, številska polja, končna polja, funkcijska polja in p-adična polja.
• velik del teorije singularnosti je posvečen singularnostim algebrskih varietet.
• računalniška algebrska geometrija je področje, ki se je pojavilo na stičišču algebrske geometrije in računalniške algebre z vzponom računalnikov. Sestoji se predvsem iz načrtovanja algoritmov in razvoja programske opreme za raziskovanje značilnosti eksplicitno danih algebrskih varietet.

Velik del razvoja glavnega toka algebrske geometrije v 20. stoletju se je zgodil znotraj okvira abstraktne algebre, pri čemer je bil vedno večji poudarek na »vrojenih« značilnostih algebrskih varietet, ki niso odvisne od nobenega posebnega načina vgrajevanja varietete v okoljski koordinatni prostor – to je vzporedno z razvojem topologije, diferencialne in kompleksne geometrije. Eden ključnih dosežkov te abstraktne algebrske geometrije je Grothendieckova teorija shem, ki omogoča uporabo teorije snopov za raziskovanje algebrskih varietet na način, ki je zelo podoben njeni rabi pri raziskovanju diferencialnih in analitičnih mnogoterosti. To se pridobi z razširitvijo pojma točke – v klasični algebrski geometriji se lahko točko afine varietete po Hilbertovem izreku o ničlah identificira z maksimalnim idealom koordinatnega kolobarja, medtem ko so točke ustrezne afine sheme vse praideali tega kolobarja. To pomeni, da je točka takšne sheme lahko bodisi običajna točka bodisi podvarieteta. Ta pristop omogoča tudi poenotenje jezika in orodij klasične algebrske geometrije, ki se v glavnem ukvarja s kompleksnimi točkami, in algebrske teorije števil. Wilesov dokaz dolgotrajne domneve, imenovane Fermatov veliki izrek, je zgled moči takšnega pristopa.

Osnovni pojmi

Več informacij: algebrska varieteta

Ničle simultanih polinomov

Enotska krožnica

Enotska sfera in poševna krožnica

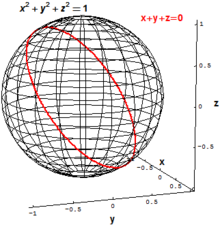
V klasični algebrski geometriji so glavni predmeti zanimanja izginjajoče množice zbirk polinomov, kar pomeni množico vseh točk, za katere hkrati velja ena ali več polinomskih enačb. Enotska krožnica v dvorazsežnem evklidskem prostoru $\mathbb {R} ^{2}\!\,$ se lahko na primer definira kot množica vseh točk $(x,y)\!\,$ s polinomsko enačbo:

$x^{2}+y^{2}-1=0\!\,,$

Podobno se lahko definira enotska sfera – dvorazsežna sfera s polmerom 1 v trirazsežnem evklidskem prostoru $\mathbb {R} ^{3}\!\,$ kot množica vseh točk $(x,y,z)\!\,$ s polinomsko enačbo:

$x^{2}+y^{2}+z^{2}-1=0\!\,.$

»Poševna« krožnica v $\mathbb {R} ^{3}\!\,$ se lahko definira kot množica vseh točk $(x,y,z)\!\,$, za ketere veljata polinomski enačbi:

$x^{2}+y^{2}+z^{2}-1=0\!\,,$

$x+y+z=0\!\,.$

Afine varietete

Najprej se obravnava polje (komutativni obseg) $k\!\,$. V klasični algebrski geometriji je bilo to polje vedno polje kompleksnih števil $\mathbb {C} \!\,$, vendar je veliko istih rezultatov resničnih, če se predpostavi le, da je $k\!\,$ algebrsko zaprt. Upošteva se afini prostor razsežnosti $n\!\,$ nad $k\!\,$, označen z $\mathbf {A} ^{n}(k)\!\,$ (ali preprosteje $\mathbf {A} ^{n}\!\,$, ko je pomen $k\!\,$ jasen iz konteksta). Ko se določi koordinatni sistem, se lahko $\mathbf {A} ^{n}(k)\!\,$ identificira s $k^{n}\!\,$. Namen nedelovanja s $k^{n}\!\,$ je poudariti, da se »pozablja« struktura vektorskega prostora, ki jo nosi $k^{n}\!\,$.

Funkcija $f:\mathbf {A} ^{n}\to \mathbf {A} ^{1}\!\,$ je polinomska (ali regularna), če se jo lahko zapiše kot polinom, to je, če obstaja polinom $p\!\,$ v $k\left[x_{1},\cdots ,x_{n}\right]\!\,$, tako da velja $f(M)=p(t_{1},\cdots ,t_{n}\!\,$) za vsako točko $M\!\,$ s koordinatami $(t_{1},\cdots ,t_{n}\!\,$) v $\mathbf {A} ^{n}\!\,$. Značilnost funkcije, da je polinomska (ali regularna), ni odvisna od izbire koordinatnega sistema v $\mathbf {A} ^{n}\!\,$.

Ko je koordinatni sistem izbran, se lahko regularne funkcije na afinem n-prostoru identificira s kolobarjem polinomskih funkcij $n\!\,$ spremenljivk nad $k\!\,$. Zato je množica regularnih funkcij na $\mathbf {A} ^{n}\!\,$ kolobar, ki se ga označi s $k\left[\mathbf {A} ^{n}\right]\!\,$.

Polinom izgine v točki, če njegovo vrednotenje v tej točki da nič. Naj bo $S\!\,$ množica polinomov v $k\left[\mathbf {A} ^{n}\right]\!\,$. Izginjajoča množica $S\!\,$ (ali izginjajoče geometrijsko mesto točk ali ničelna množica) je množica $V(S)\!\,$ vseh točk v $\mathbf {A} ^{n}\!\,$, kjer vsak polinom iz $S\!\,$ izgine. Ali simbolično:

$V(S)=\{(t_{1},\cdots ,t_{n})\mid p(t_{1},\cdots ,t_{n})=0{\text{ za vse }}p\in S\}\!\,.$

Podmnožica $\mathbf {A} ^{n}\!\,$, ki je $V(S)\!\,$, za neko množico $S\!\,$, se imenuje algebrska množica. $V\!\,$ pomeni varieteto (posebno vrsto algebrske množice, ki bo definirana spodaj).

Ali se lahko glede na dano podmnožico $U\!\,$ množice $\mathbf {A} ^{n}\!\,$ obnovi množico polinomov, ki jo generirajo? Če je $U\!\,$ poljubna podmnožica $\mathbf {A} ^{n}\!\,$, se definira $I(U)\!\,$ kot množico vseh polinomov, katerih izginjajoča množica vsebuje $U\!\,$. $I\!\,$ pomeni ideal – če dva polinoma $f\!\,$ in $g\!\,$ oba izgineta na $U\!\,$, potem $f+g\!\,$ izgine na $U\!\,$, in če je $h\!\,$ poljubni polinom, potem $hf\!\,$ izgine na $U\!\,$, tako da je $I(U)\!\,$ vedno ideal polinomskega kolobarja $k\left[\mathbf {A} ^{n}\right]\!\,$.

Postavita se lahko dve naravni vprašanji:

• kdaj za dano podmožico $U\!\,$ množice $\mathbf {A} ^{n}\!\,$ velja $U=V(I(U))\!\,$?
• kdaj za dano množico polinomov $S\!\,$ velja $S=I(V(S))\!\,$?

Odgovor na prvo vprašanje daje uvedba topologije Zariskega, topologije na $\mathbf {A} ^{n}\!\,$, katere zaprte množice so algebrske množice in ki neposredno odraža algebrsko strukturo $k\left[\mathbf {A} ^{n}\right]\!\,$. Potem je $U=V(I(U))\!\,$, če in samo če je $U\!\,$ algebrska množica ali enakovredno zaprta množica po Zariskem. Odgovor na drugo vprašanje daje Hilbertov izrek o ničlah. V eni od svojih oblik pravi, da je $I(V(S))\!\,$ radikal ideala, ki ga generira $S\!\,$. V bolj abstraktnem jeziku obstaja Galoisova povezava, ki povzroči dva operatorja zaprtja – mogoče ju je identificirati in imata seveda osnovno vlogo v teoriji. Zgled je razdelan pri Galoisovi povezavi.

Zaradi različnih razlogov se morda ne želi vedno delati s celotnim idealom, ki ustreza algebrski množici $U\!\,$. Hilbertov izrek o bazi implicira, da so ideali v $k\left[\mathbf {A} ^{n}\right]\!\,$ vedno končno generirani.

Algebrska množica se imenuje ireducibilna, če je ni mogoče zapisati kot unijo dveh manjših algebrskih množic. Vsaka algebrska množica je končna unija ireducibilnih algebrskih množic in ta dekompozicija je edinstvena. Zato se njeni elementi imenujejo ireducibilne komponente algebrske množice. Ireducibilna algebrska množica se imenuje tudi varieteta. Izkaže se, da je algebrska množica varieteta, če in samo če se jo lahko definira kot izginjajočo množico praideala polinomskega kolobarja.

Nekateri avtorji ne razlikujejo jasno med algebrskimi množicami in varietetami in za razlikovanje uporabljajo ireducibilno varieteto, kadar je to potrebno.

Regularne funkcije

Tako kot so zvezne funkcije naravne preslikave na topoloških prostorih in gladke funkcije naravne preslikave na diferenciabilnih mnogoterostih, obstaja naravni razred funkcij na algebrski množici, ki se imenuje regularne funkcije ali polinomske funkcije. Regularna funkcija na algebrski množici $V\!\,$, ki jo vsebuje $\mathbf {A} ^{n}\!\,$, je omejitev na $V\!\,$ regularne funkcije na $\mathbf {A} ^{n}\!\,$. Za algebrsko množico, definirano na polju kompleksnih števil, so regularne funkcije gladke in celo analitične.

Morda se zdi nenaravno omejujoče zahtevati, da se regularna funkcija vedno razširi na okoljski prostor, vendar je zelo podobno stanju v normalnem topološkem prostoru, kjer Tietzejev razširitveni izrek zagotavlja, da se zvezna funkcija na zaprti podmnožici vedno razširi na okoljski topološki prostor.

Tako kot regularne funkcije na afinem prostoru tudi regularne funkcije na $V\!\,$ tvorijo kolobar, ki se ga označi s $k\left[V\right]\!\,$. Ta kolobar se imenuje koordinatni kolobar $V\!\,$.

Ker regularne funkcije na $V\!\,$ izvirajo iz regularnih funkcij na $\mathbf {A} ^{n}\!\,$, obstaja razmerje med koordinatnimi kolobarji. Še posebej, če je regularna funkcija na $V\!\,$ omejitev dveh funkcij $f\!\,$ in $g\!\,$ v $k\left[\mathbf {A} ^{n}\right]\!\,$, potem je $f-g\!\,$ polinomska funkcija, ki je enaka nič na $V\!\,$ in tako pripada $I(V)\!\,$. Tako se lahko $k\left[V\right]\!\,$ identificira s $k\left[\mathbf {A} ^{n}\right]/I(V)\!\,$.

Morfizem afinih varietet

Z uporabo regularnih funkcij iz afine varietete v $\mathbf {A} ^{1}\!\,$ se lahko definira regularne preslikave iz ene afine varietete v drugo. Najprej se definira regularno preslikavo iz varietete v afini prostor. Naj bo $V\!\,$ varieteta, ki jo vsebuje $\mathbf {A} ^{n}\!\,$. Izbere se $m\!\,$ regularnih funkcij na $V\!\,$ in se jih poimenuje $f_{1},\cdots ,f_{m}\!\,$. Regularna preslikava $f\!\,$ iz $V\!\,$ v $\mathbf {A} ^{m}\!\,$ se definira tako, da velja $f=(f_{1},\cdots ,f_{m})\!\,$. Ali z drugimi besedami, vsaka $f_{i}\!\,$ določa eno koordinato območja $f\!\,$.

Če je $V'\!\,$ varieteta, ki jo vsebuje $\mathbf {A} ^{m}\!\,$, je $f\!\,$ regularna preslikava iz $V\!\,$ v $V'\!\,$, če $V'\!\,$ vsebuje območje $f\!\,$.

Definicija regularnih preslikav velja tudi za algebrske množice. Regularne preslikave se imenujejo tudi morfizmi, saj tvorijo zbirko vseh afinih algebrskih množic v kategorijo, kjer so objekti afine algebrske množice, morfizmi pa so regularne preslikave. Afine varietete so podkategorija kategorije algebrskih množic.

Glede na dano regularno preslikavo $g\!\,$ iz $V\!\,$ v $V'\!\,$ in regularno funkcijo $f\!\,$ od $k\left[V'\right]\!\,$ velja $f\circ g\in k\left[V\right]\!\,$. Preslikava $f\to f\circ g\!\,$ je homomorfizem kolobarjev iz $k\left[V'\right]\!\,$ v $k\left[V\right]\!\,$. Nasprotno pa vsak homomorfizem kolobarjev iz $k\left[V'\right]\!\,$ v $k\left[V\right]\!\,$ definira regularno preslikavo iz $V\!\,$ v $V'\!\,$. To definira ekvivalenco kategorij med kategorijo algebrskih množic in nasprotno kategorijo končno generiranih reduciranih k-algeber. Ta ekvivalenca je eno od izhodišč teorije shem.

Racionalna funkcija in biracionalna ekvivalenca

V nasprotju s prejšnjimi razdelki se ta razdelek nanaša le na varietete in ne na algebrske množice. Po drugi strani pa se definicije naravno razširijo na projektivne varietete (naslednji razdelek), saj imata afina varieteta in njena projektivna zapolnitev isto polje funkcij.

Če je $V\!\,$ afina varieteta, je njen koordinatni kolobar celostna domena in ima torej polje ulomkov, ki se ga označi s $k(V)\!\,$ in se imenuje polje racionalnih funkcij na $V\!\,$ ali, na kratko, funkcijsko polje $V\!\,$. Njegovi elementi so omejitve na $V\!\,$ racionalnih funkcij nad afinim prostorom, ki vsebuje $V\!\,$. Domena racionalne funkcije $f\!\,$ ni $V\!\,$, ampak komplement podvarietete (hiperploskve), kjer imenovalec $f\!\,$ izgine.

Kot pri regularnih preslikavah se lahko definira racionalno preslikavo iz varietete $V\!\,$ v varieteto $V'\!\,$. Kot pri regularnih preslikavah se lahko racionalne preslikave iz $V\!\,$ v $V'\!\,$ identificira s homomorfizmi polj iz $k(V')\!\,$ v $k(V)\!\,$.

Dve afini varieteti sta biracionalno ekvivalentni, če sta med njimi dve racionalni funkciji, ki sta inverzni druga drugi v območjih, kjer sta obe definirani. Enakovredno sta biracionalno ekvivalentni, če sta njuni funkcijski polji izomorfni.

Afina varieteta je racionalna varieteta, če je biracionalno ekvivalentna afinemu prostoru. To pomeni, da varieteta dopušča racionalno parametrizacijo, to je parametrizacijo z racionalnimi funkcijami. Na primer krožnica enačbe $x^{2}+y^{2}-1=0\!\,$ je racionalna krivulja, saj ima parametrično enačbo:

$x={\frac {2\,t}{1+t^{2}}}\!\,$

$y={\frac {1-t^{2}}{1+t^{2}}}\!\,,$

na katero se lahko gleda kot na racionalno preslikavo iz premice na krožnico.

Problem razrešitve singularnosti je vedeti, ali je vsaka algebrska varieteta biracionalno ekvivalentna varieteti, katere projektivna zapolnitev je nesingularna (glej tudi gladka zapolnitev). Heisuke Hironaka ga je leta 1964 rešil pritrdilno v karakteristiki 0, v končni karakteristiki $p\!\,$ pa je še nerešen v razsežnostih vsaj 4.

Projektivna varieteta

Parabola ($y=x^{2}\!\,$, rdeče) in kubična krivulja ($y=x^{3}\!\,$, modro) v projektivnem prostoru

Tako kot formule za ničle polinomov druge, tretje in četrte stopnje kažejo razširitev realnih števil na bolj algebrsko popolno ozadje kompleksnih števil, številne značilnosti algebrskih varietet kažejo razširitev afinega prostora na geometrično popolnejši projektivni prostor. Medtem ko se kompleksna števila dobi z dodajanjem števila i, ničle polinoma druge stopnje $x^{2}+1\!\,$, se projektivni prostor dobi z dodajanjem ustreznih točk »v neskončnosti«, točk, kjer se vzporedne premice lahko srečajo.

Če se želi videti, kako bi lahko prišlo do tega, je treba razmisliti o varieteti $V(y-x^{2})\!\,$. Če se jo nariše, se dobi parabolo. Ko gre $x\!\,$ v pozitivno neskončnost, gre tudi naklon premice od izhodišča do točke $(x,x^{2})\!\,$ v pozitivno neskončnost. Ko gre $x\!\,$ v negativno neskončnost, gre naklon iste premice v negativno neskončnost.

Če se primerja to z varieteto $V(y-x^{3})\!\,$, je to kubična krivulja. Ko gre $x\!\,$ v pozitivno neskončnost, gre naklon premice od izhodišča do točke $(x,x^{3})\!\,$ v pozitivno neskončnost tako kot prej. Toda za razliko od prej gre $x\!\,$, ko gre v negativno neskončnost, tudi naklon iste premice v pozitivno neskončnost – pravo nasprotje parabole. Torej se obnašanje »v neskončnosti« varietete $V(y-x^{3})\!\,$ razlikuje od obnašanja »v neskončnosti« variete $V(y-x^{2})\!\,$.

Upoštevanje projektivne zapolnitve obeh krivulj, ki je njuno podaljšanje »v neskončnost« v projektivni ravnini, omogoča kvantificiranje te razlike: točka v neskončnosti parabole je regularna točka, katere tangenta je premica v neskončnosti, medtem ko je točka v neskončnosti kubične krivulje njena točka obrata. Prav tako sta obe krivulji racionalni, saj sta parametrizirani z $x\!\,$, Riemann-Rochov izrek pa implicira, da mora imeti kubična krivulja singularnost, ki mora biti v neskončnosti, saj so vse njene točke v afinem prostoru regularne.

Tako je veliko značilnosti algebrskih varietet, vključno z biracionalno ekvivalenco in vsemi topološkimi značilnostmi, odvisnih od obnašanja »v neskončnosti«, zato je naravno preučevanje varietet v projektivnem prostoru. Poleg tega je uvedba projektivnih tehnik naredila številne izreke v algebrski geometriji preprostejše in ostrejše. Bézoutov izrek o številu presečišč med dvema varietetama je na primer mogoče navesti v najostrejši obliki samo v projektivnem prostoru. Zaradi teh razlogov ima projektivni prostor osnovno vlogo v algebrski geometriji.

Sedaj je projektivni prostor $P^{n}\!\,$ razsežnosti $n\!\,$ običajno definiran kot množica premic skozi točko, ki velja za izhodišče, v afinem prostoru razsežnosti $n+1\!\,$, ali enakovredno množici vektorskih premic v vektorskem prostoru razsežnosti $n+1\!\,$. Ko je koordinatni sistem v prostoru razsežnosti $n+1\!\,$ izbran, imajo vse točke premice enako množico koordinat do množenja z elementom $k\!\,$. To definira homogene koordinate točke prostora $P^{n}\!\,$ kot zaporedje $n+1\!\,$ elementov osnovnega polja $k\!\,$, definiranega do množenja z neničelnim elementom $k\!\,$ (enako za celotno zaporedje).

Polinom $n+1\!\,$ spremenljivk izgine v vseh točkah premice, ki poteka skozi izhodišče, če in samo če je homogen. V tem primeru polinom izgine v ustrezni točki prostora $\mathbf {P} ^{n}\!\,$. To omogoča definicijo projektivne algebrske množice v $\mathbf {P} ^{n}\!\,$ kot množico $V(f_{1},\cdots ,f_{k})\!\,$, kjer končna množica homogenih polinomov $\{f_{1},\cdots ,f_{k}\}\!\,$ izgine. Tako kot pri afinih algebrskih množicah obstaja bijekcija med projektivnimi algebrskimi množicami in reduciranimi homogenimi ideali, ki jih definirajo. Projektivne varietete so projektivne algebrske množice, katerih definirajoči ideal je praideal. Z drugimi besedami, projektivna varieteta je projektivna algebrska množica, katere homogeni koordinatni kolobar je celostna domena, pri čemer je projektivni koordinatni kolobar definiran kot kvocient graduiranega kolobarja ali polinomov $n+1\!\,$ spremenljivk s homogenim (reduciranim) idealom, ki definira varieteto. Vsako projektivno algebrsko množico je mogoče enolično razstaviti v končno unijo projektivnih varietet.

Edine regularne funkcije, ki jih je mogoče pravilno definirati na projektivni varieteti, so konstantne funkcije. Tako se ta pojem ne uporablja v projektivnih razmerah. Po drugi strani pa je uporaben pojem polja racionalnih funkcij oziroma funkcijskega polja, ki se ga podobno kot afini primer definira kot množico kvocientov dveh homogenih elementov enake stopnje v homogenem koordinatnem kolobarju.

Realna algebrska geometrija

Realna algebrska geometrija je preučevanje realnih točk algebrskih varietet.

Pri takšnem raziskovanju ni mogoče prezreti dejstva, da je polje realnih števil urejeno polje. Na primer, krivulja enačbe $x^{2}+y^{2}-a=0\!\,$ je krožnica, če je $a>0\!\,$, vendar nima realne točke, če je $a<0\!\,$. Iz tega sledi, da realna algebrska geometrija ni le preučevanje realnih algebrskih varietet, ampak so jo posplošili na preučevanje polalgebrskih množic, ki so rešitve sistemov polinomskih enačb in polinomskih neenačb. Veja hiperbole z enačbo $xy-1=0\!\,$ na primer ni algebrska varieteta, ampak je polalgebrska množica, definirana z $xy-1=0\!\,$ in $x>0$ ali z $xy-1=0\!\,$ in $x+y>0\!\,$.

Eden od zahtevnih problemov realne algebrske geometrije je nerešen Hilbertov šestnajsti problem: odločitev katere posamezne lege so možne za ovale nesingularne ravninske krivulje stopnje 8.

Računalniška algebrska geometrija

Izvor računalniške algebrske geometrije se lahko datira na srečanje EUROSAM'79 (Mednarodni simpozij o simbolični in algebrski manipulaciji), ki je potekal v Marseillu v Franciji junija 1979. Na tem srečanju je:

• Dennis Soulé Arnon pokazal, da valjna algebrska dekompozicija (CAD) Georgea Edwina Collinsa omogoča izračunavanje topologije polagebrskih množic,
• Bruno Buchberger predstavil Gröbnerjeve baze in svoj algoritem za njihovo izračunavanje,
• Daniel Lazard predstavil novi algoritem za reševanje sistemov homogenih polinomskih enačb z računsko zahtevnostjo, ki je v bistvu polinomska v pričakovanem številu rešitev in tako preprosto eksponentna glede števila neznank. Ta algoritem je močno povezan z rezultanto z več spremenljivkami Francisa Sowerbyja Macaulaya.

Od tedaj je večina rezultatov na tem področju povezana z eno ali več od teh postavk bodisi z uporabo ali izboljšanjem enega od teh algoritmov ali z iskanjem algoritmov, katerih zahtevnost je preprosto eksponentna glede na število spremenljivk.

V zadnjih nekaj desetletjih so razvili sklop matematične teorije, ki dopolnjuje simbolične metode, imenovane numerična algebrska geometrija. Glavna računska metoda je homotopsko nadaljevanje. To podpira na primer model izračunavanja s plavajočo vejico za reševanje problemov algebrske geometrije.

Gröbnerjeva baza

Gröbnerjeva baza je sistem generatorjev polinomskega ideala, katerega izračunavanje omogoča dedukcijo mnogih značilnosti afine algebrske varietete, ki jo ideal definira.

Če je dani ideal $I\!\,$, ki definira algebrsko množico $V\!\,$:

• je $V\!\,$ prazna (čez algebrsko zaprto razširitev baznega polja), če in samo če je Gröbnerjeva baza za katero koli monomsko urejanje reducirana na {1}.
• je s pomočjo Hilbertove vrste mogoče izračunati razsežnost in stopnjo množice $V\!\,$ iz katere koli Gröbnerjeve baze ideala $I\!\,$ za monomsko urejanje, ki izboljša celotno stopnjo.
• in, če je razsežnost $V\!\,$ enaka 0, se lahko izračuna (končno število) točk $V\!\,$ iz katere koli Gröbnerjeve baze ideala $I\!\,$ (glej sistem polinomskih enačb).
• izračunavanje z Gröbnerjevo bazo omogoča, da se iz $V\!\,$ odstrani vse nereducibilne komponente, ki jih vsebuje dana hiperploskev.
• izračunavanje z Gröbnerjevo bazo omogoča izračun zaprtja Zariskega slike množice $V\!\,$ s projekcijo na $k\!\,$ prvih koordinat in podmnožice slike, kjer projekcija ni prava.
• izračunavanja z Gröbnerjevo bazo bolj splošno omogočajo izračun zaprtja Zariskega slike in kritičnih točk racionalne funkcije množice $V\!\,$ v drugo afino varieteto..

Izračunavanja z Gröbnerjevo bazo ne omogočajo neposrednega izračuna primarne dekompozicije ideala $I\!\,$ niti praidealov, ki definirajo ireducibilne komponente $V\!\,$, vendar večina algoritmov za to vključuje izračunavanje Gröbnerjeve baze. Algoritmi, ki ne temeljijo na Gröbnerjevih bazah, uporabljajo regularne verige, vendar lahko v nekaterih izjemnih primerih potrebujejo Gröbnerjeve baze.

Gröbnerjeve baze veljajo za težko izračunljive. Pravzaprav lahko v najslabšem primeru vsebujejo polinome, katerih stopnja je dvojno eksponentna glede na število spremenljivk, in število polinomov, ki je prav tako dvojno eksponentno. Vendar je to le zahtevnost v najslabšem primeru in pogosto se lahko uporablja zahtevnostna meja Lazardovega algoritma iz leta 1979. Faugèrov algoritem F5 uresničuje to zahtevnost, saj se ga lahko razume kot izboljšavo Lazardovega algoritma iz leta 1979. Iz tega sledi, da najboljše izvedbe omogočajo skoraj rutinsko izračunavanje z algebrskimi množicami stopnje več kot 100. To pomeni, da je trenutno težava pri izračunavanju Gröbnerjeve baze močno povezana z vrojeno težavnostjo problema.

Valjna algebrska dekompozicija (CAD)

Valjna algebrska dekompozicija (CAD, cylindrical algebraic decomposition) je algoritem, ki ga je leta 1973 uvedel Collins za izvedbo s sprejemljivo zahtevnostjo izreka Tarskega in Seidenberga o eliminaciji kvantifikatorja nad realnimi števili.

Ta izrek se nanaša na formule logike prvega reda, katerih atomarne formule so polinomske enakosti ali neenakosti med polinomi z realnimi koeficienti. Te formule so torej formule, ki jih je mogoče sestaviti iz atomarnih formul z logičnimi operatorji in (∧), ali (∨), ne (¬), za vse (∀) in obstaja (∃). Izrek Tarskega in Seidenberga trdi, da je mogoče iz takšne formule izračunati enakovredno formulo brez kvantifikatorja (∀, ∃).

Zahtevnost CAD je dvojno eksponentna glede na število spremenljivk. To pomeni, da CAD v teoriji omogoča rešitev vsakega problema realne algebrske geometrije, ki ga je mogoče izraziti s takšno formulo, to je skoraj vsak problem, ki zadeva eksplicitno dane varietete in polalgebrske množice.

Medtem ko ima izračunavanje Gröbnerjeve baze dvojno eksponentno zahtevnost le v redkih primerih, ima CAD skoraj vedno tako visoko zahtevnost. To pomeni, da morda ne bo rešila problemov z več kot štirimi spremenljivkami, razen če je večina polinomov, ki se pojavljajo na vhodu, linearnih.

Od leta 1973 je večina raziskav na to temo posvečena bodisi izboljšanju CAD bodisi iskanju alternativnih algoritmov v posebnih primerih splošnega pomena.

Kot zgled najvišje ravni razvoja obstajajo učinkoviti algoritmi za iskanje vsaj točke v vsaki povezani komponenti polalgebrske množice in s tem za preverjanje, ali je polalgebrska množica prazna. Po drugi strani pa je CAD v praksi še vedno najboljši algoritem za štetje števila povezanih komponent.

Asimptotična zahtevnost proti praktični učinkovitosti

Osnovni splošni algoritmi računalniške geometrije imajo dvojno eksponentno zahtevnost v najslabšem primeru. Točneje, če je $d\!\,$ največja stopnja vhodnih polinomov in $n\!\,$ število spremenljivk, je njihova zahtevnost največ $d^{2^{cn}}\!\,$ za poljubno konstanto $c\!\,$ in za nekatere vnose je zahtevnost vsaj $d^{2^{c'n}}\!\,$ za drugo konstanto $c'\!\,$.

V zadnjih 20 letih 20. stoletja so uvedli različne algoritme za reševanje specifičnih podproblemov z boljšo zahtevnostjo. Večina teh algoritmov ima zahtevnost $d^{O(n^{2})}\!\,$.

Med temi algoritmi, ki rešujejo podproblem problema, rešenega z Gröbnerjevo bazo, se lahko navede: testiranje ali je afina varieteta prazna, in reševanje nehomogenih polinomskih sistemov s končnim številom rešitev. Takšni algoritmi se redko izvajajo, ker imata pri večini vnosov Faugèrova algoritma F4 in F5 boljšo praktično učinkovitost in verjetno podobno ali boljšo zahtevnost (verjetno zato, ker je vrednotenje zahtevnosti algoritmov na osnovi Gröbnerjeve baze na določenem razredu vnosov težka naloga, ki so jo naredili le v nekaj posebnih primerih).

Glavni algoritmi realne algebrske geometrije, ki rešujejo problem, rešenega s CAD, so povezani s topologijo polalgebrskih množic. Kot zglede se lahko navede: štetje števila povezanih komponent, testiranje, ali sta dve točki v istih komponentah, ali izračun Whitneyjeve stratifikacije realne algebrske množice. Imajo zahtevnost $d^{O(n^{2})}\!\,$, vendar je vrednost konstante, ki jo vključuje zapis O, tako visoka, da je njihova uporaba za reševanje katerega koli netrivialnega problema, ki ga učinkovito rešuje CAD, nemogoča, tudi če bi se lahko uporabila vsa obstoječa računalniška moč na svetu. Zato te algoritme niso nikoli izvedli in to je dejavno raziskovalno področje iskanja algoritmov, ki imajo skupaj dobro asimptotično zahtevnost in dobro praktično učinkovitost.

Abstraktni moderni vidik

Moderni pristopi k algebrski geometriji ponovno definirajo in učinkovito razširijo obseg osnovnih objektov na različnih ravneh splošnosti na sheme, formalne sheme, ind-sheme, algebrske prostore, algebrske sklade in tako naprej. Potreba po tem izhaja že iz uporabnih zamisli znotraj teorije varietet, npr. formalne funkcije Zariskega je mogoče prilagoditi z uvedbo nilpotentnih elementov v strukturne kolobarje; upoštevanje prostorov zank in lokov, konstruiranje kvocientov z grupnimi akcijami in razvijanje formalnih podlag za naravno teorijo presekov in teorijo deformacij vodijo do nekaterih nadaljnjih razširitev.

Najbolj presenetljivo je, da so bile v poznih 1950-ih algebrske varietete vključene v Grothendieckov koncept shem. Njihovi krajevni objekti so afine sheme ali praspektri, krajevno okolobarjeni prostori, ki tvorijo kategorijo, antiekvivalentni kategoriji komutativnih unitalnih kolobarjev, kar razširja dualnost med kategorijo afinih algebrskih varietet nad poljem $k\!\,$ in kategorijo končno generiranih reduciranih k-algeber. Lepljenje poteka po topologiji Zariskega. Lahko se zlepi znotraj kategorije krajevno okolobarjenih prostorov, pa tudi, z uporabo Jonedovega vgrajevanja, znotraj bolj abstraktne kategorije predsnopov množic nad kategorijo afinih shem. Topologijo Zariskega v smislu teorije množic nato nadomesti Grothendieckova topologija. Grothendieck je uvedel Grothendieckove topologije, pri čemer je imel v mislih bolj eksotične, a geometrično točnejše in občutljivejše primere kot surova topologija Zariskega, namreč topologijo étale in dve ploski Grothendieckovi topologiji: fppf in fpqc. Sedaj so nekateri drugi primeri postali pomembni, vključno s Nisnevičevo topologijo. Snope je mogoče nadalje posplošiti na sklade v smislu Grothendiecka, običajno z nekaterimi dodatnimi pogoji predstavljivosti, ki vodijo do Artinovih skladov in, še finejših, Deligne-Mumfordovih skladov, ki se pogosto imenujejo algebrski skladi.

Včasih druga algebrska mesta nadomestijo kategorijo afinih shem. Nikolaj Valerjevič Durov je na primer uvedel komutativne algebrske monade kot posplošitev krajevnih objektov v posplošeni algebrski geometriji. V tej postavitvi so bile realizirane različice tropske geometrije, absolutne geometrije nad poljem enega elementa in algebrskega analoga geometrije Arakelova.

Druga formalna posplošitev je možna za univerzalno algebrsko geometrijo, v kateri ima vsaka varieteta algeber svojo lastno algebrsko geometrijo. Izraza varieteta algeber se ne sme zamenjevati z algebrsko varieteto.

Jezik shem, skladov in posplošitev se je izkazal za dragocen način obravnave geometrijskih konceptov in je postal temelj sodobne algebrske geometrije.

Algebrske sklade je mogoče nadalje posplošiti in za mnoga praktična vprašanja, kot sta teorija deformacij in teorija presekov, je to pogosto najbolj naraven pristop. Grothendieckovo mesto afinih shem se lahko razširi na višje kategorično mesto izpeljanih afinih shem z zamenjavo komutativnih kolobarjev z neskončno kategorijo diferencialno graduiranih komutativnih algeber ali simplicialnih komutativnih kolobarjev ali podobno kategorijo z ustrezno različico Grothendieckove topologije. Lahko se tudi zamenja predsnope množic s predsnopi simplicialnih množic (ali neskončnih grupoidov). Nato se lahko ob prisotnosti ustreznega homotopskega stroja razvije pojem izpeljanega sklada kot takega predsnopa na neskončni kategoriji izpeljanih afinih shem, ki zadošča določeni neskončni kategorični različici aksioma snopa (in da je algebrsko, induktivno zaporedje pogojev zastopljivosti). Quillenove kategorije modelov, Segalove kategorije in kvazikategorije so nekatera od najpogosteje uporabljenih orodij za formalizacijo tega, ki dajejo izpeljano algebrsko geometrijo. Uvedla jo je šola Carlosa Simpsona, vključno z Andreom Hirschowitzem, Bertrandom Toënom, Gabrielleom Vezzosijem, Michelom Vaquiéjem in drugimi. Nadalje so jo razvili Jacob Lurie, Toën in Vezzosi. Drugo (nekomutativno) različico izpeljane algebrske geometrije, ki uporablja kategorije A-neskončnosti, so v zgodnjih 1990-ih razvili Maksim Lvovič Koncevič in njegovi privrženci.

Zgodovina

Pred 16. stoletjem

Nekatere korenine algebrske geometrije segajo v delo starih Grkov iz 5. stoletja pr. n. št. Delski problem je bil na primer skonstruirati takšno dolžino $x\!\,$ tako bo imela kocka s stranico $x\!\,$ enako prostornino kot pravokotna škatla $a^{2}b\!\,$ za dani stranici $a\!\,$ in $b\!\,$. Menehmo (okoli 350 pr. n. št.) je problem obravnaval geometrično s presekom para ravninskih stožnic $ay=x^{2}\!\,$ in $xy=ab\!\,$.

V 3. stoletju pr. n. št. sta Arhimed in Apolonij sistematično preučevala dodatne probleme na stožnicah z uporabo koordinat. Apolonij je v delu O stožnicah nadalje razvil metodo, ki je tako podobna analitični geometriji, da včasih domnevajo, da je njegovo delo napovedovalo delo Renéja Descartesa za približno 1800 let. Njegova uporaba referenčnih premic, premera in tangente se v bistvu ne razlikuje od moderne uporabe koordinatnega okvira, kjer so razdalje, izmerjene vzdolž premera od dotikališča, abscise, daljice, vzporedne s tangento in potekajoče med osjo in krivuljo, pa so ordinate. Naprej je razvil zveze med abscisami in ustreznimi koordinatami z uporabo geometrijskih metod, kot je uporaba parabol in krivulj.

Srednjeveški matematiki, vključno z Omarjem Hajamom, Leonardom Fibonaccijem, Levijem ben Geršomom in Nicolom Oresmom v srednjeveškem obdobju, so nekatere kubične in kvadratne enačbe reševali s čisto algebrskimi sredstvi in rezultate nato interpretirali geometrijsko. Hajam (rojen leta 1048) je verjel, da obstaja povezava med aritmetiko, algebro in geometrijo. To je kritiziral Jeffrey Alan Oaks, profesor matematike na Univerzi v Indianapolisu, ki trdi, da preučevanje krivulj s pomočjo enačb izvira od Descartesa v 17. stoletju.

Renesansa

Takšne tehnike uporabe geometrijskih konstrukcij pri algebrskih problemih so sprejeli tudi številni renesančni matematiki, kot sta Gerolamo Cardano in Niccolo Fontana Tartaglia, pri svojih raziskovanjih kubične enačbe. Večina matematikov iz 16. in 17. stoletja je bila naklonjena geometrijskemu pristopu h konstrukcijskim problemom namesto algebrskega, zlasti Blaise Pascal, ki je nasprotoval uporabi algebrskih in analitičnih metod v geometriji. Francoski matematiki François Viète in kasneje Descartes ter Pierre de Fermat so z uvedbo koordinatne geometrije revolucionirali običajen način razmišljanja o konstrukcijskih problemih. Zanimale so jih predvsem značilnosti algebrskih krivulj, kot so tiste, ki jih definirajo diofantske enačbe (v primeru Fermata), in algebrska reformulacija klasičnih grških del o stožnicah in kubikih (v primeru Descartesa).

V istem obdobju sta Pascal in Gérard Desargues pristopila h geometriji z drugačne perspektive in razvila sintetične pojme projektivne geometrije. Prav tako sta preučevala krivulje, vendar s čisto geometrijskega vidika kot analog starogrške konstrukcije z ravnilom in šestilom. Končno je zmagala Descartesova in Fermatova analitična geometrija, saj je matematike iz 18. stoletja oskrbela s konkretnimi kvantitativnimi orodji, potrebnimi za preučevanje fizikalnih problemov z uporabo novega računa Isaaca Newtona in Gottfrieda Wilhelma Leibniza. Vendar pa je do konca 18. stoletja večino algebrskega značaja koordinatne geometrije prevzel infinitezimalni račun Joseph-Louisa Lagrangea in Leonharda Eulerja.

19. in zgodnje 20. stoletje

Potreben je bil hkratni razvoj neevklidske geometrije in Abelovih integralov v 19. stoletju, da so se stare algebrske zamisli vrnile nazaj v geometrijsko krilo. Prvega od teh novih razvojev sta izkoristila Edmond Nicolas Laguerre in Arthur Cayley, ki sta poskušala ugotoviti splošne metrične značilnosti projektivnega prostora. Cayley je uvedel zamisel o homogenih polinomskih formah, in še posebej o kvadratnih formah, na projektivnem prostoru. Pozneje je Felix Christian Klein preučeval projektivno geometrijo (skupaj z drugimi vrstami geometrije) z vidika, da je geometrija na prostoru kodirana v določenem razredu transformacij na prostoru. Do konca 19. stoletja so projektivni geometri proučevali bolj splošne vrste transformacij na figurah v projektivnem prostoru. Namesto projektivnih linearnih transformacij, za katere se je običajno štelo, da dajejo fundamentalno Kleinovo geometrijo na projektivnem prostoru, so se ukvarjali tudi z biracionalnimi transformacijami višje stopnje. Ta šibkejši pojem kongruence je člane italijanske šole algebrske geometrije 20. stoletja pozneje vodil h klasifikaciji algebrskih ploskev do biracionalnega izomorfizma.

Drugi razvoj zgodnjega 19. stoletja, razvoj Abelovih integralov, je pripeljal Bernharda Riemanna do razvoja Riemannovih ploskev.

V tem času je bila algebrska geometrija bolj ali manj sopomenka za raziskovanje invariant. Invariante v tem pomenu so bile količine, ki se ostajale nespremenjene pri linearnih transformacijah koordinat – kolineacij v starejši terminologiji. Zgled so diskriminante, kot je diskriminanta kvadratne funkcije $b^{2}-ac\!\,$. David Hilbert je rešil večino problemov klasične teorije invariant v nizu člankov v zgodnjih 1890-ih. V njih je uvedel več novih algebrskih metod.

V istem obdobju se je začela algebraizacija algebrske geometrije s pomočjo komutativne algebre. Izstopajoči rezultati v tej smeri so Hilbertov izrek o bazi in Hilbertov izrek o ničlah, ki sta osnova povezave med algebrsko geometrijo in komutativno algebro, ter Macaulayeva rezultanta z več spremenljivkami, ki je osnova eliminacijske teorije. Verjetno zaradi velikosti izračunavanja, ki ga implicirajo rezultante z več spremenljivkami, so sredi 20. stoletja na eliminacijsko teorijo pozabili, dokler je nista obnovili teorija singularnosti in računalniška algebrska geometrija.

20. stoletje

Bartel Leendert van der Waerden, Oscar Zariski in André Weil so razvili osnovo za algebrsko geometrijo, ki temelji na sodobni komutativni algebri, vključno s teorijo vrednotenja in teorijo idealov. Eden od ciljev je bil podati strog okvir za dokazovanje rezultatov italijanske šole algebrske geometrije. Predvsem je ta šola sistematično uporabljala pojem generične točke brez kakršne koli točne definicije, ki so ga ti avtorji prvi podali v 1930-ih.

V 1950-ih in 1960-ih sta Jean-Pierre Serre in Grothendieck prenovila temelje z uporabo teorije snopov. Kasneje, približno od leta 1960, in v veliki meri pod vodstvom Grothendiecka, se je razvila zamisel o shemah v povezavi z zelo izpopolnjenim aparatom homolognih tehnik. Po desetletju hitrega razvoja se je področje v 1970-ih stabiliziralo in pojavile so se nove aplikacije, tako za teorijo števil kot tudi za bolj klasična geometrijska vprašanja o algebrskih varietetah, singularnostih, modulih in formalnih modulih.

Pomemben razred varietet, ki jih ni enostavno razumeti neposredno iz njihovih definirajočih enačb, so abelovske varietete, ki so projektivne varietete, katerih točke tvorijo Abelovo grupo. Prototipski primeri so eliptične krivulje, ki imajo bogato teorijo. Bile so ključnega pomena pri dokazu Fermatovega velikega izreka in se uporabljajo tudi v kriptografiji z eliptičnimi krivuljami.

Vzporedno z abstraktnim trendom algebrske geometrije, ki se ukvarja s splošnimi izjavami o varietetah, so se razvile tudi metode za učinkovito izračunavanje s konkretno danimi varietetami, ki vodijo v novo področje računalniške algebrske geometrije. Ena izmed temeljnih metod tega področja je teorija Gröbnerjevih baz, ki jo je uvedel Bruno Buchberger leta 1965. Druga temeljna metoda, ki je bolj posvečena realni algebrski geometriji, je valjna algebrska dekompozicija (CAD), ki jo je leta 1973 uvedel George Edwin Collins.

Glej tudi: izpeljana algebrska geometrija.

Analitična geometrija

(Kompleksna) analitična varieteta je definirana krajevno kot množica skupnih rešitev več enačb, ki vključujejo analitične funkcije. Je analogna vključenemu konceptu realne ali kompleksne algebrske varietete. Vsaka kompleksna mnogoterost je analitična varieteta. Ker imajo lahko analitične varietete singularne točke, niso vse analitične varietete mnogoterosti.

Moderna analitična geometrija je v bistvu enakovredna realni in kompleksni algebrski geometriji, kot je pokazal Serre leta 1956 v svojem članku GAGA, katerega ime je francosko za algebrsko geometrijo in analitično geometrijo. Kljub temu obe področji ostajata različni, saj so dokazovalne metode precej različne in algebrska geometrija vključuje tudi geometrijo v končni karakteristiki.

Uporabe

Algebrska geometrija se zdaj uporablja v algebrski statistiki, teoriji nadzora, robotiki, kodah za popravljanje napak (Goppovih kodah), računalniški filogenetiki in geometrijskem modeliranju. Obstajajo tudi povezave s homologno zrcalno simetrijo v teoriji strun, teorijo iger, ujemanji v teoriji grafov, solitoni in celoštevilskim programiranjem.

Glej tudi

• glosar klasične algebrske geometrije
• pomembne publikacije v algebrski geometriji
• seznam kompleksnih in algebrskih ploskev
• nekomutativna algebrska geometrija
• enumerativna geometrija

Sklici

Viri

• Baker, Greg (2013), »Complexity of Algorithms«, www.cs.sfu.ca (v angleščini), Univerza Simona Fraserja, pridobljeno 12. julija 2022
• Blume, Lawrence Edward; Zame, William Robin (Julij 1994), »The algebraic geometry of perfect and sequential equilibrium«, Econometrica, 62 (4): 783–794, doi:10.2307/2951732, JSTOR 2951732
• Cipra, Barry Arthur (2007), »Algebraic Geometers See Ideal Approach to Biology« (PDF), SIAM News, 40 (6), arhivirano iz prvotnega spletišča (PDF) dne 3. marca 2016
• Cox, David Archibald; Sturmfels, Bernd (1998), Manocha, Dinesh N. (ur.), Applications of Computational Algebraic Geometry, Ameriško matematično društvo, ISBN 978-0-8218-6758-7
• Cox, David Archibald; Katz, Sheldon H. (1999), Mirror Symmetry and Algebraic Geometry, Ameriško matematično društvo, ISBN 978-0-8218-2127-5, OCLC 880847689
• Dieudonné, Jean (Oktober 1972), »The Historical Development of Algebraic Geometry«, American Mathematical Monthly, 79 (8): 827–866, doi:10.2307/2317664, JSTOR 2317664, Wikipodatki Q55886951
• Drton, Mathias; Sturmfels, Bernd; Sullivant, Seth (2009), Lectures on Algebraic Statistics, (Oberwolfach seminars), zv. 39, Basel ; Boston ; Berlin: Birkäuser Verlag, COBISS 15723865, ISBN 978-3-7643-8904-8, ISSN 1661-237X, OCLC 15723865
• Falb, Peter Lawrence (1999), Methods of Algebraic Geometry in Control Theory : Part II : Multivariable Linear Systems and Projective Algebraic Geometry, Boston: Birkhäuser, ISBN 978-0-8176-4113-9, OCLC 21160575
• Fordy, Allan P., ur. (1990), Soliton Theory: A Survey of Results, Manchester University Press, ISBN 978-0-7190-1491-8, OCLC 20296833
• Hauser, Herwig (2010), »On the problem of resolution of singularities in positive characteristic (Or: a proof we are still waiting for)«, Bulletin of the American Mathematical Society, New Series, 47 (1): 1–30, doi:10.1090/S0273-0979-09-01274-9, MR 2566444
• Hironaka, Heisuke (1964), »Resolution of Singularities of an Algebraic Variety Over a Field of Characteristic Zero: I«, Annals of Mathematics, 2, 79 (1): 109–203, doi:10.2307/1970486, JSTOR 1970486, MR 0199184 in II. del, str. 205–326, JSTOR 1970547
• Jüttler, Bert; Piene, Ragni (2008), Geometric Modeling and Algebraic Geometry, Berlin ; Heidelberg: Springer-Verlag, COBISS 1540182751, ISBN 978-3-540-72185-7, OCLC 255726249
• Kenyon, Richard; Okounkov, Andrei; Sheffield, Scott (2003). »Dimers and Amoebae«. arXiv:math-ph/0311005.
• Kline, Morris (1972), Mathematical Thought from Ancient to Modern Times, zv. 1, Oxford University Press, COBISS 5758728, ISBN 0-19-506135-7, OCLC 827616096
• M., G. B. (6. avgust 1896), »Apollonius of Perga: Treatise on Conic Sections«, Nature (v angleščini), 54 (1397): 314–315, Bibcode:1896Natur..54..314G, doi:10.1038/054314a0, ISSN 1476-4687, S2CID 4059946
• Molland, Andrew George (1. februar 1976), »Shifting the foundations: Descartes's transformation of ancient geometry«, Historia Mathematica (v angleščini), 3 (1): 21–49, doi:10.1016/0315-0860(76)90004-5, ISSN 0315-0860
• Oaks, Jeffrey Alan (Januar 2016), »Excavating the errors in the "Mathematics" : Chapter of 1001 Inventions«, v Brentjes, Sonja; Edis, Taner; Richter-Bernburd, Lutz (ur.), 1001 Distortions: How (Not) to Narrate History of Science, Medicine, and Technology in Non-Western Cultures, Würzburg: Ergon-Verlag, str. 151–171, ISBN 978-3-95650-169-2, OCLC 960886495, arhivirano iz spletišča dne 27. februarja 2021
• O'Connor, John Joseph; Robertson, Edmund Frederick (Julij 1999), »Apollonius of Perga«, Arhiv zgodovine matematike MacTutor (v angleščini), Šola za matematiko in statistiko, Univerza v St Andrewsu, pridobljeno 11. novembra 2022
• O'Connor, John Joseph; Robertson, Edmund Frederick (Julij 1999), »Omar Khayyam«, Arhiv zgodovine matematike MacTutor (v angleščini), Šola za matematiko in statistiko, Univerza v St Andrewsu, arhivirano iz prvotnega spletišča dne 12. novembra 2017, Zdi se, da je Hajam sam prvi zasnoval splošno teorijo kubičnih enačb.
• Rashed, Roshdi (1994), The Development Of Arabic Mathematics : Between Arithmetic And Algebra, (Boston Studies in the Philosophy and History of Science), zv. 156, prevod: Armstrong, Angela F. W., Dordrecht: Springer Science+Business Media, str. 102–103, doi:10.1007/978-94-017-3274-1, ISBN 978-90-481-4338-2, OCLC 851372484
• Selig, Jonathan M. (2005), Geometric Fundamentals of Robotics, (Monographs in Computer Science) (2. izd.), New York: Springer-Verlag, doi:10.1007/b138859, ISBN 978-0-387-20874-9, ISSN 0172-603X, OCLC 262679866
• Serre, Jean-Pierre (1956), »Géométrie algébrique et géométrie analytique«, Annales de l'Institut Fourier (v francoščini), 6: 1–42, doi:10.5802/aif.59, ISSN 0373-0956, MR 0082175, Zbl 0075.30401
• Unguru, Sabetai (Junij 1976), »A Very Early Acquaintance with Apollonius of Perga's Treatise on Conic Sections in the Latin West«, Centaurus (v angleščini), 20 (2): 112–128, Bibcode:1976Cent...20..112U, doi:10.1111/j.1600-0498.1976.tb00924.x, ISSN 0008-8994
• Tannenbaum, Allen Robert (1981), Invariance and Systems Theory: Algebraic and Geometric Aspects, (Lecture Notes in Mathematics), zv. 845, Berlin ; Heidelberg ; New York: Springer-Verlag, COBISS 3628121, ISBN 978-3-540-10565-7, OCLC 7274480
• Tsfasman, Michael Anatol'evich; Vlăduț, Serge G.; Nogin, Dmitry (1990), Algebraic Geometric Codes Basic Notions, Ameriško matematično društvo, ISBN 978-0-8218-7520-9

Nadaljnje branje

Nekateri klasični učbeniki, starejši od shem

• van der Waerden, Bartel Leendert (1945), Einfuehrung in die algebraische Geometrie, Dover
• Hodge, William Vallance Douglas; Pedoe, Daniel (1994), Methods of Algebraic Geometry Volume 1, Cambridge University Press, ISBN 978-0-521-46900-5, Zbl 0796.14001
• Hodge, William Vallance Douglas; Pedoe, Daniel (1994), Methods of Algebraic Geometry Volume 2, Cambridge University Press, ISBN 978-0-521-46901-2, Zbl 0796.14002
• Hodge, William Vallance Douglas; Pedoe, Daniel (1994), Methods of Algebraic Geometry Volume 3, Cambridge University Press, ISBN 978-0-521-46775-9, Zbl 0796.14003

Moderni učbeniki, ki ne uporabljajo jezika shem

• Garrity, Thomas Anthony; Belshoff, Richard; Boos, Lynette; Brown, J. Ryan; Lienert, Carl; Murphy, David; Navarra-Madsen, Junalyn; Poitevin, Pedro; Robinson, Shawn; Snyder, Brian; Werner, Caryn (2013), Algebraic Geometry A Problem Solving Approach, (Student mathematical library ; volume 66. IAS/Park City mathematical subseries), Providence: Ameriško matematično društvo, COBISS 17279065, ISBN 978-0-821-89396-8, OCLC 815043206
• Griffiths, Phillip; Harris, Joe (1994), Principles of Algebraic Geometry, Wiley-Interscience, ISBN 978-0-471-05059-9, Zbl 0836.14001
• Harris, Joe (1995), Algebraic Geometry A First Course, Springer-Verlag, ISBN 978-0-387-97716-4, Zbl 0779.14001
• Mumford, David (1995), Algebraic Geometry I Complex Projective Varieties (2. izd.), Springer-Verlag, ISBN 978-3-540-58657-9, Zbl 0821.14001
• Reid, Miles (1988), Undergraduate Algebraic Geometry, Cambridge University Press, ISBN 978-0-521-35662-6, Zbl 0701.14001
• Šafarevič, Igor Rostislavovič (1995), Basic Algebraic Geometry I Varieties in Projective Space (2. izd.), Springer-Verlag, ISBN 978-0-387-54812-8, Zbl 0797.14001

Učbeniki iz računalniške algebrske geometrije

• Cox, David Archibald; Little, John; O'Shea, Donal (1997), Ideals, Varieties, and Algorithms (2. izd.), Springer-Verlag, ISBN 978-0-387-94680-1, Zbl 0861.13012
• Schenck, Hal (2003), Computational Algebraic Geometry, Cambridge University Press
• Basu, Saugata; Pollack, Richard; Roy, Marie-Françoise (2006), Algorithms in real algebraic geometry, Springer-Verlag
• González-Vega, Laureano; Recio, Tómas (1996), Algorithms in algebraic geometry and applications, Birkhaüser
• Elkadi, Mohamed; Mourrain, Bernard; Piene, Ragni, ur. (2006), Algebraic geometry and geometric modeling, Springer-Verlag
• Dickenstein, Alicia; Schreyer, Frank-Olaf; Sommese, Andrew J., ur. (2008), Algorithms in Algebraic Geometry, (The IMA Volumes in Mathematics and its Applications), zv. 146, Springer, ISBN 9780387751559, LCCN 2007938208
• Cox, David Archibald; Little, John B.; O'Shea, Donal (1998), Using algebraic geometry, Springer-Verlag
• Caviness, Bob F.; Johnson, Jeremy R. (1998), Quantifier elimination and cylindrical algebraic decomposition, Springer-Verlag

Učbeniki in reference za sheme

• Eisenbud, David; Harris, Joe (1998), The Geometry of Schemes, Springer-Verlag, ISBN 978-0-387-98637-1, Zbl 0960.14002
• Grothendieck, Alexander (1960), Éléments de géométrie algébrique, Publications Mathématiques de l'IHÉS, Zbl 0118.36206
• Grothendieck, Alexander; Dieudonné, Jean Alexandre (1971), Éléments de géométrie algébrique, zv. 1 (2. izd.), Springer-Verlag, ISBN 978-3-540-05113-8, Zbl 0203.23301
• Hartshorne, Robin (1977), Algebraic Geometry, Springer-Verlag, ISBN 978-0-387-90244-9, Zbl 0367.14001
• Mumford, David (1999), The Red Book of Varieties and Schemes Includes the Michigan Lectures on Curves and Their Jacobians (2. izd.), Springer-Verlag, ISBN 978-3-540-63293-1, Zbl 0945.14001
• Šafarevič, Igor Rostislavovič (1995), Basic Algebraic Geometry II Schemes and complex manifolds (2. izd.), Springer-Verlag, ISBN 978-3-540-57554-2, Zbl 0797.14002

Zunanje povezave

• Foundations of Algebraic Geometry by Ravi Vakil, 808 pp.
• Algebraic geometry entry on PlanetMath
• English translation of the van der Waerden textbook
• Dieudonné, Jean (3. marec 1972). »The History of Algebraic Geometry« (v angleščini). Pogovor na Oddelku za matematiko Univerze Wisconsina-Milwaukee. Arhivirano iz spletišča dne 22. novembra 2021 – prek YouTube.
• The Stacks Project, an open source textbook and reference work on algebraic stacks and algebraic geometry