Verižnica

Viseča veriga ima obliko krivulje, ki ji pravimo verižnica.

Verižnice z različnimi parametri.

Verižnica (tudi katenioda) je ravninska transcendentna krivulja, ki jo po umiritvi zavzame tanka, neraztegljiva homogena in prosto viseča nit ali veriga.

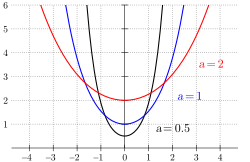
Krivulja ima obliko hiperboličnega kosinusa. Podobna je paraboli, čeprav se od nje matematično močno razlikuje. Rotacijska ploskev, ki jo da verižnica, je katenoid, ki spada med minimalne ploskve.

Beseda katenoida izvira iz latinske besede catena, kar pomeni veriga.

Verižnica v kartezičnih koordinatah

V kartezičnem koordinatnem sistemu je

$y = {a \over 2}( e^{x/a}+e^{-x/a} ) = a ~ \operatorname{ch} {x \over a}$

kjer je

• $\operatorname{ch}$ hiperbolični kosinus
• $a \,$ konstanta.

Whewellova enačba za verižnico je

$\tan \varphi = \frac{s}{a}$.

Cesárojeva enačba pa je

$\kappa=\frac{a}{s^2+a^2}$.

kjer je

• $\kappa$ ukrivljenost
• $s \,$ dolžina loka
• $a \,$ konstanta (glej zgoraj)

Polmer ukrivljenosti je

$\rho = a \sec^2 \varphi$

Parametrična oblika enačbe verižnice

V kartezični parametrični obliki je enačba verižnice

$x = a \text { }\ln \text { } t$

$y = \frac {a} {2} (t + 1/t)$

kjer je $t > 0 \,$

Tri različne verižnice, odvisne od horizontalne sile $\scriptstyle T_H$, pri tem pa je $\scriptstyle a = \lambda H/T_H$ kjer je λ masa na enoto dolžine.

Sile, ki delujejo na del verižnice od c do r. Sile so napetost T₀ v točki c, napetost T v točki r in teža verige (0, −λgs). Ker veriga miruje, mora biti vsota teh sil enaka nič.

Lastnosti

• verižnice so si med seboj podobne. S spreminjanjem parametra $a \,$ dosežemo samo skaliranje krivulje (povečevanje ali zmanjševanje).
• kvadratna kolesa se lahko vrtijo po cestišču, ki bi imelo izbokline z obliko obrnjene verižnice.
• naboj v enakomernem električnem polju se giblje vzdolž verižnice, ki postane parabola, če je hitrost naboja mnogo manjša od hitrosti svetlobe.
• ploščina, ki jo omejuje verižnica in dve ordinati ter abscisna os je enaka

$S = a^2 (\operatorname{sh}{x_2 \over a} - \operatorname{sh}{x_1 \over a}) = a (\sqrt{y_2^2-a^2} - \sqrt{y_1^2-a^2})$

Glej tudi

• katenoid
• seznam krivulj

Zunanje povezave

• Kvadratno kolo, verižnica in traktrisa (v slovenščini)
• Veriga in obok v Presek-u (v slovenščini)
• Kaj je verižnica (v slovenščini)
• Verižnica na MathWorld (v angleščini)
• Verižnica na PlanetMath (v angleščini)
• Verižnica v Encyclopédie des Formes Mathématiques Remarquables (v francoščini)
• Natančnejše izračunavanje verižnice (v francoščini)