Logaritemska spirala
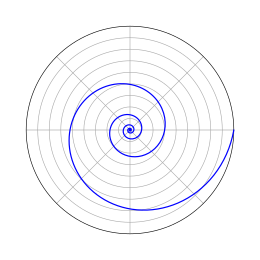

Logaritemska spirala (tudi enakokotna spirala in spirala rasti) je vrsta spirale, ki se pogosto pojavlja v naravi.
Logaritemsko spiralo je prvi opisal francoski filozof, matematik, fizik, učenjak in častnik René Descartes (1596–1650), pozneje pa še švicarski matematik Jakob Bernoulli I. (1654–1705), ki jo je imenoval spira mirabilis (čudežna krivulja).
Logaritemska spirala v polarnih koordinatah[uredi | uredi kodo]
V polarnem koordinatnem sistemu je:
ali:
kjer je:
- osnova naravnih logaritmov
- pozitivna realna konstanta
- pozitivna realna konstanta
Parametrična oblika[uredi | uredi kodo]
Parametrična oblika enačbe logaritemske spirale je:
kjer sta in realni konstanti.
Značilnosti[uredi | uredi kodo]
- kot med tangento in premico v smeri polmera v točki je konstanten.
- od Arhimedove spirale se razlikuje v tem, da pri logaritemski spirali razdalje med posameznimi obrati tvorijo geometrijsko zaporedje, pri Arhimedovi spirali pa so konstantne.
- logaritemska spirala je skladna sama s seboj pri vseh podobnostnih transformacijah. Skaliranje s faktorjem da isti rezultat kot je original, samo brez vrtenja. Spirale so tudi skladne s svojimi evolventami, evolutami in nožiščnimi krivuljami.
- če se nariše zlato spiralo (to je logaritemska spirala, ki raste navzven za faktorje enake zlatemu rezu za vsakih 90° vrtenja) ali kar je približno kot, da bi se uporabilo Fibonaccijeva števila.
- če se prične pot v neki točki in se giblje proti notranjosti spirale oziroma proti izhodišču, se naredi poljubno število obratov, ne da bi se doseglo izhodišče, pa pri tem pa se naredi končno pot. Skupna pot, ki se pri tem naredi, je enaka , kjer je razdalja točke od izhodišča. To značilnost je odkril že italijanski fizik in matematik Evangelista Torricelli (1608 – 1647).
Splošna oblika logaritemske spirale [1][uredi | uredi kodo]
Splošna oblika logaritemske spirale v polarnih koordinatah je:
kjer sta in realni števili. V tem obrazcu ni uporabljena osnova naravnih logaritmov , ampak poljubna osnova .
Logaritemska spirala v naravi[uredi | uredi kodo]
V naravi je izredno veliko primerov, kjer se najde logaritemsko spiralo. Navedenih je le nekaj primerov:
- približevanje jastreba žrtvi.
- približevanje žuželk izvoru svetlobe
- rokavi spiralnih galaksij
- živci roženice
- rokavi tropskih ciklonov
- biološke strukture (lupine mehkužcev).
Glej tudi[uredi | uredi kodo]
Sklici[uredi | uredi kodo]
Zunanje povezave[uredi | uredi kodo]
- Zlati rez (slovensko)
- Logaritemske spirala na 2dcurves.com (angleško)
- Weisstein, Eric Wolfgang. »Logarithmic Spiral«. MathWorld.
- Logaritemska spirala Arhivirano 2011-08-05 na Wayback Machine. na PlanethMath (angleško)
- Logaritemska spirala v Encyclopédie des Formes Mathématiques Remarquable (francosko)
- Spirale Arhivirano 2012-02-17 na Wayback Machine. na Spiralzoom (angleško)
- Logaritemska spirala na JSXGraph (angleško)














