Naravni logaritem

Potek funkcije naravnega logaritma. Funkcija počasi raste proti pozitivni neskončnosti, ko x narašča in gre proti negativni neskončnosti, ko se x približuje 0 (»počasneje« in »hitreje« kot katerakoli potenca x). Y-os je asimptota.

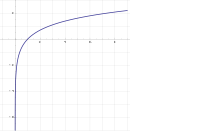
Naravni logaritem je logaritem z osnovo e, ki je iracionalna in transcendentna konstanta. Vrednost te konstante je približno 2,718 281 828. Naravni logaritem označujemo z ln(x), log_e(x). Včasih tudi, če je osnova e sama po sebi razumljiva, kot log(x) .

Naravni logaritem števila $x \,$ je potenca s katero moramo potencirati število e, da bi dobili x. Naravni logaritem vrednosti e je enak 1 (ln(e) = 1), ker je e¹ = 1. Naravni logaritem od 1 je 0 ((ln(1) = 0).

Naravni logaritem lahko definiramo za katerokoli pozitivno realno število $a \,$.

Funkcija naravnega logaritma, če jo obravnavamo kot funkcijo realne spremenljivke, je inverzna funkcija eksponentne funkcije, kar zapišemo na naslednji način

$e^{\ln(x)} = x \qquad \mbox{kadar je}\quad x > 0\,\!$

ali

$\ln(e^x) = x.\,\!$

Podobno kot za vse logaritme, tudi za naravne logaritme velja

$\ln(xy) = \ln(x) + \ln(y) \!\,$

s tem pa lahko preslikamo množenje v seštevanje. To pomeni, da je logaritemska funkcija izomorfizem iz grupe realnih pozitivnih števil pod množenjem v grupo realnih števil pod množenjem. To lahko prikažemo s funkcijo

$\ln : \mathbb{R}^+ \to \mathbb{R}.$

Definicije

Funkcija ln(a), prikazana kot ploskev pod krivuljo f(x) = 1/x od 1 do a. Kadar je a manjši od 1, se ploskev od a do 1 obravnava kot negativna.

Prvi način definiranja naravnega logaritma:

Naravni logaritem ln(a)lahko definiramo kot integral

$\ln(a)=\int_1^a \frac{1}{x}\,dx.$

Ta funkcija je logaritem, ker zadošča pogoju

$\ln(ab)=\ln(a)+\ln(b) \,\!$

Drugi način definiranja naravnega logaritma je v tem, da najprej definiramo eksponentno funkcijo (n. pr kot neskončno vrsto). Naravni logaritem potem definiramo kot inverzno funkcijo.

Značilnosti

• $\ln(1) = 0\,$

• $\ln(-1) = i \pi \quad \,$

(glej kompleksni logaritem)

• $\ln(x) < \ln(y) \quad{\rm za}\quad 0 < x < y\;$

• $\frac{h}{1+h} \leq \ln(1+h) \leq h \quad{\rm za}\quad h > -1\;$

• $\lim_{x \to 0} \frac{\ln(1+x)}{x} = 1\,$.

Odvod

Odvod naravnega logaritma je dan z

$\frac{d}{dx} \ln(x) = \frac{1}{x}\,$.

Taylorjeva vrsta

To pa neposredno vodi do Taylorjeve vrste za $\ln(x + 1)$ okoli 0, kar je znano kot Mercatorjeva vrsta

$\ln(1+x)=\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n} x^n = x - \frac{x^2}{2} + \frac{x^3}{3} - \cdots \quad{\rm za}\quad \left|x\right| \leq 1\quad$

${\rm razen \quad za}\quad x = -1$

Integriranje

Naravni logaritem omogoča integracijo funkcije, ki ima obliko g(x) = f'(x)/f(x). Primitivna funkcija od g(x) je dana z ln(|f(x)|). To velja zaradi pravila načina odvajanja sestavljene funkcije in zveze

$\ {d \over dx}\left( \ln \left| x \right| \right) = {1 \over x}.$

ali

$\int { 1 \over x} dx = \ln|x| + C$

in

$\int { \frac{f'(x)}{f(x)}\, dx} = \ln |f(x)| + C.$

Številska vrednost

Da bi izračunali vrednost naravnega logaritma poljubnega števila, lahko Taylorjevo vrsto zapišemo v obliki

$\ln(1+x)= x \,\left( \frac{1}{1} - x\,\left(\frac{1}{2} - x \,\left(\frac{1}{3} - x \,\left(\frac{1}{4} - x \,\left(\frac{1}{5}- \cdots \right)\right)\right)\right)\right) \quad{\rm za}\quad \left|x\right|<1.\,\!$

Boljšo konvergenco dobimo, če uporabimo

$\ln(x) = \ln\left(\frac{1+y}{1-y}\right)$	$= 2\,y\, \left( \frac{1}{1} + \frac{1}{3} y^{2} + \frac{1}{5} y^{4} + \frac{1}{7} y^{6} + \frac{1}{9} y^{8} + \cdots \right)$
	$= 2\,y\, \left( \frac{1}{1} + y^{2} \, \left( \frac{1}{3} + y^{2} \, \left( \frac{1}{5} + y^{2} \, \left( \frac{1}{7} + y^{2} \, \left( \frac{1}{9} + \cdots \right) \right) \right)\right) \right)$

To pa dosežemo, če je y =(x – 1)/(x + 1) in x>0.

Naravni logaritem števila 10

Naravni logaritem števila 10 izračunamo kot

$\ln (a\times 10^n) = \ln a + n \ln 10.$

Verižni ulomki

Enostavni verižni ulomki niso znani. So pa znani posplošeni verižni ulomki, kot je na primer:

$\log(1+x)=\frac{x^1}{1}-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+\frac{x^5}{5}-\cdots= \cfrac{x}{1-0x+\cfrac{1^2x}{2-1x+\cfrac{2^2x}{3-2x+\cfrac{3^2x}{4-3x+\cfrac{4^2x}{5-4x+\ddots}}}}}$

$\log \left( 1+\frac{2x}{y} \right) = \cfrac{2x} {y+\cfrac{x} {1+\cfrac{x} {3y+\cfrac{2x} {1+\cfrac{2x} {5y+\cfrac{3x} {1+\ddots}}}}}} = \cfrac{2x} {y+x-\cfrac{(1x)^2} {3(y+x)-\cfrac{(2x)^2} {5(y+x)-\cfrac{(3x)^2} {7(y+x)-\ddots}}}}$

Kompleksni logaritmi

Eksponentno funkcijo lahko razširimo na funkcije, ki dajo kompleksno število kot e^x za poljubno kompleksno število x. Eksponentno funkcijo lahko obrnemo tako, da tvorimo kompleksni logaritem, ki ima večino lastnosti običajnih logaritmov. Pri tem pa nastopita dve težavi. Ne obstoja x, za katerega bi veljalo e^x = 0. Prav tako velja e^2πi = 1 = e⁰.

Tako logaritmi ne morejo biti definirani za celotno kompleksno ravnino.

• Grafi naravnega logaritma v kompleksni ravnini (glavna veja)
• 

  z = Re(ln(x+iy))

• 

  z = Im(ln(x+iy))

• 

  z = |ln(x+iy)|

• 

  Superpozicija treh grafov.

Zunanje povezave

• Naravni logaritem na MathWorld (v angleščini)
• Naravni logaritem na BetterExplained (v angleščini)