Zlata spirala

Zlata spirala je ravninska krivulja, ki se jo v polarnem koordinatnem sistemu (r, θ) opiše z enačbo:
kjer sta število zlatega reza (zlato razmerje) in Ludolfovo število.
Konstrukcijo zlate spirale se približno izvede v zlatem pravokotniku s pomočjo četrtinskih lokov včrtanih krožnic v posamezna polja zlatega pravokotnika. Razdelitev zlatega pravokotnika na takšna polja prikazuje Slika 1:

Včrtavanje četrtinskih lokov krožnic znotraj zlatoreznih polj kaže Slika 2:
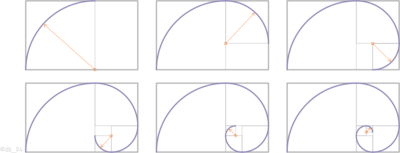
Polmeri lokov predstavljajo padajoče geometrijsko zaporedje s količnikom, enakim obratni vrednosti zlatega razmerja
oblike
Zlata spirala spada v družino logaritemskih spiral (predlog za ime logaritemska spirala je podal francoski matematik Pierre Varignon (1645–1722)). Pomembna značilnost logaritemskih spiral je, da kot, ki ga tangenta na spiralo v poljubni točki oklepa z radijvektorjem, ostaja konstanten. Tako se lahko logaritemske spirale imenuje tudi enakokotne spirale (Slika 3).

Poleg Enačbe 1 je za zlato spiralo izpeljanih še več enačb, med njimi je zelo uporabna Sharpova:
kjer je:
Točka, ki predstavlja začetek zlate spirale (bolje rečeno njeno stekališče), ima koordinati:
kjer je e poljubno izbrana enota za višino zlati spirali očrtanega zlatega pravokotnika.
Poleg omenjene konstrukcije zlate spirale znotraj zlatega pravokotnika so znane še druge, alternativne konstrukcije zlate spirale, denimo v zlatem trikotniku, zlatem petkotniku in podobne. Obstaja še konstrukcija velike zlate spirale s pomočjo tričetrtinskih krožnih lokov na zlatem pravokotniku. To prikazuje Slika 5.

Glej tudi[uredi | uredi kodo]
Zunanje povezave[uredi | uredi kodo]








