Wattova krivulja
Videz
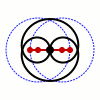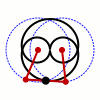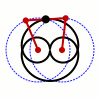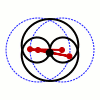
Wattova krivulja je ravninska krivulja šeste stopnje (sekstična krivulja: glej stopnja polinoma). Nastane s pomočjo dveh krožnic s polmerom , ki imata središči oddaljeni . Daljica z dolžino je pritrjena na neki točki v vsaki od obeh krožnic. Pri tem sredina daljice opisuje Wattovo krivuljo med tem, ko se kroga vrtita (oziroma, ko se konca daljice vrtita po obeh krožnicah).
Imenuje se po škotskem matematiku, inženirju in izumitelju Jamesu Wattu (1736 – 1819).
Krivulja v polarnih koordinatah
[uredi | uredi kodo]V polarnem koordinatnem sistemu je enačba Wattove krivulje:
Krivulja v kartezičnih koordinatah
[uredi | uredi kodo]V kartezičnem koordinatnem sistemu je enačba Wattove kriulje:
Če pa se zapiše d2=a2+b2-c2, se dobi enostavnejšo obliko:
Zunanje povezave
[uredi | uredi kodo]- Weisstein, Eric Wolfgang. »Watt's Curve«. MathWorld.
- Wattova krivulja na MacTutor (angleško)
- Wattova krivulja v Encyclopédie des Formes Mathématiques Remarquables (francosko)
- Wattova krivulja na 2dcurves.com (angleško)




![{\displaystyle r^{2}=b^{2}-\left[a\sin \theta \pm {\sqrt {c^{2}-a^{2}\cos ^{2}\theta }}\right]^{2}\!\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4628bf6834e8a53aa47d158948682ab9700b281c)

