Riemannova domneva

Riemannova domneva je v matematiki domneva, da imajo vse netrivialne ničle Riemannove funkcije ζ realni del enak 1/2. Predlagal jo je Bernhard Riemann leta 1859.[1] Ime domneve je povezano tudi z nekaterimi drugimi zelo sorodnimi pojmi, kot na primer Riemannova domneva o krivuljah v končnih obsegih.
Riemannova domneva obsega rezultate o porazdelitvi praštevil. Skupaj z ustreznimi posplošitvami jo imajo nekateri matematiki za najpomembnejši nerešeni problem v čisti matematiki.[2] Riemannova domneva je skupaj z Goldbachovo domnevo del Hilbertovega osmega problema na Hilbertovem seznamu 23-ih nerešenih problemov iz leta 1900. Kot edini problem s Hilbertovega seznama je uvrščena tudi med problemi tisočletne nagrade Clayjevega matematičnega inštituta.
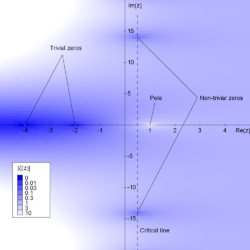
Riemannova funkcija ζ(s) je funkcija, katere argument s je lahko poljubno kompleksno število različno od 1 in katere vrednosti so tudi kompleksne. Njene ničle se pojavljajo pri negativnih sodih celih številih – , kadar je Te ničle se imenujejo trivialne ničle. Odvod Riemannove funkcije ζ v trivialnih ničlah je dan analitično:[3][4]
tako da se predznak odvoda izmenično spreminja. Vendar te ničle niso edine vrednosti za katere je vrednost funkcije ζ enaka nič. Druge ničle se imenujejo netrivialne ničle. Riemannova domneva zadeva lege teh netrivialnih ničel in pravi:
- da je realni del vseh netrivialnih ničel Riemannove funkcije ζ enak 12 (), oziroma enakovredno, za .[5]
V novejšem času se k zgornji definiciji doda pogoj, da so netrivialne ničle enostavne, kar pomeni, da je v njih odvod različen od nič:[4]
Če je domneva pravilna, tako vse netrivialne ničle ležijo na kritični premici, ki vsebuje kompleksna števila , kjer je t realno število, i pa imaginarna enota, in so enostavne. Zapis je standarden že od Riemannovega izvirnega članka.[6] Sicer se rabijo tudi drugačni zapisi, na primer še posebej za netrivialne ničle . Prve vrednosti t so:
| n |
|
OEIS |
A013629 |
A002410 |
A092783 |
A153595 |
A161914 |
|---|---|---|---|---|---|---|---|
| 1 | 14,134725141734... | A058303 | 14 | 14 | 15 | 14 | 14 |
| 2 | 21,022039638771... | A065434 | 21 | 21 | 22 | 6 | 7 |
| 3 | 25,010857580145... | A065452 | 25 | 25 | 26 | 3 | 4 |
| 4 | 30,424876125859... | A065453 | 30 | 30 | 31 | 5 | 5 |
| 5 | 32,935061587739... | A192492 | 32 | 33 | 33 | 2 | 3 |
| 6 | 37,586178158825... | A305741 | 37 | 38 | 38 | 4 | 5 |
| 7 | 40,918719012147... | A305742 | 40 | 41 | 41 | 3 | 3 |
| 8 | 43,327073280914... | A305743 | 43 | 43 | 44 | 2 | 2 |
| 9 | 48,005150881167... | A305744 | 48 | 48 | 49 | 4 | 5 |
| 10 | 49,773832477672... | A306004 | 49 | 50 | 50 | 1 | 2 |
Iz prvih vrednosti je razvidno, da je , vendar se pri n 9137 neenakost obrne, saj je:[7]
Naslednja ničla je spet večja od n pri . Potem naprej vse do n 107 neenakost spet velja in se verjame, da velja naprej.
Riemannova funkcija ζ in njen logaritemski odvod sta povezana:[8]
kjer je Λ von Mangoldtova funkcija.
Ničle se lahko zapišejo z zaporedjem:
Rademacher je dokazal, da če je Riemannova domneva pravilna, imaginarni deli tega zaporedja tvorijo enakomerno porazdeljeno zaporedje. Hlawka je pokazal kako se lahko Rademacherjev rezultat dokaže brez privzetka o pravilnosti Riemannove domneve.[9] Rademacher-Hlawkov izrek pravi, da so za vsako realno število ulomljeni deli zaporedja:
enakomerno porazdeljeni v smislu, da za vsak podinterval del točk iz podintervala težijo k , ko gre .
O Riemannovi domnevi obstaja več netehničnih knjig, kot npr. avtorjev: Derbyshire,[10] Rockmore,[11] Sabbagh,[12][13] du Sautoy.[14] Knjige avtorjev: Edwards,[15] Patterson,[16], Borwein idr.,[17] in Mazur; Stein[18] podajajo matematični uvod, Titchmarsh,[19] Ivić,[20] in Karacuba; Voronin[21] pa so naprednejše monografije.
Riemannova funkcija ζ[uredi | uredi kodo]
Riemannova funkcija ζ je definirana za kompleksni s z realnim delom večjim od 1 z absolutno konvergentno neskončno vrsto:
Leonhard Euler je pokazal, da je ta vrsta enaka Eulerjevemu produktu:
kjer neskončni produkt poteka po vseh praštevilih p in spet konvegira za kompleksni s z realnim delom večjim od 1. Konvergenca Eulerjevega produkta kaže, da funkcija ζ(s) nima ničel v tem območju, saj je vsak faktor brez ničel.
Riemannova domneva obravnava ničle zunaj območja konvergence te vrste, zato mora zanjo obstajati analitično nadaljevanje na vse kompleksne s. To se lahko doseže, da se jo razvije z Dirichletovo funkcijo η kot sledi. Če je realni del s večji od 1, za funkcijo ζ velja:
Vendar vrsta na desni konvergira ne samo, kadar je s večji od 1, ampak splošneje kadar ima s pozitivni realni del. Ta alternativna vrsta razširja funkcijo ζ iz območja Re(s) > 1 v večjo območje Re(s) > 0 in izključuje ničle funkcij . Tudi funkcija ζ se lahko razširi na te vrednosti z limitami, ki dajo končno vrednost za vse vrednosti s s pozitivnim realnim delom , razen za enostavni pol v s = 1.
V traku 0 < Re(s) < 1 za funkcijo ζ velja funkcijska enačba:
kjer je Γ funkcija Γ. Lahko se definira ζ(s) za vsa preostala kompleksna števila s, če se privzame, da ta enačba velja tudi zunaj traku in, da je funkcija ζ(s) enaka desni strani enačbe, kadar s nima pozitivnega realnega dela. Če je s negativno celo število, potem je ζ(s) = 0, ker se faktor sin(πs/2) poniči – to so trivialne ničle funkcije ζ.[a] Vrednost ζ(0) = −1/2 ni določena s funkcijsko enačbo, ampak je limitna vrednost funkcije ζ(s), ko se s približuje ničli. Iz funkcijske enačbe tudi sledi, da funkcija ζ nima ničel z negativnim realnim delom razen trivialnih ničel, in tako vse netrivialne ničle ležijo na kritični premici, kjer ima s realni del med 0 in 1.
Ozadje in zgodovina[uredi | uredi kodo]
»…es ist sehr wahrscheinlich, dass alle Wurzeln reell sind. Hiervon wäre allerdings ein strenger Beweis zu wünschen; ich habe indess die Aufsuchung desselben nach einigen flüchtigen vergeblichen Versuchen vorläufig bei Seite gelassen, da er für den nächsten Zweck meiner Untersuchung entbehrlich schien.«
»…zelo verjetno je, da so vse ničle realne. Seveda je želja imeti tukaj dokaz; sam sem do sedaj po nekaj bežnih neuspešnih poskusih začasno dal na stran iskanje zanj, ker je verjetno nebistven za naslednji cilj moje raziskave.«
Riemannova izjava Riemannove domneve iz članka.[1] (Obravnaval je različico funkcije ζ, modificirano tako, da so njene ničle realne in ne ležijo na kritični premici.)

V svojem članku iz leta 1859 O številu praštevil, manjših od dane velikosti (Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse) je Riemann našel eksplicitne formule za število praštevil π(x) manjše od danega števila x. Njegova formula je dana s pomočjo povezane funkcije:
ki šteje praštevila in praštevilske potence do x, praštevilske potence pn kot 1/n praštevila. Število praštevil se lahko izvede iz te funkcije z:
kjer je μ Möbiusova funkcija. Riemannova formula je potem:
kjer vsota poteka po netrivialnih ničlah funkcije ζ in kjer je Π0 malo modificirana različica Π, ki zamenja njegovo vrednost v točkah neveznosti s povprečjem njegove zgornje in spodnje limite:
Vsota Riemannove formule ni absolutno konvergenta, lahko pa se izračuna z ničlami t po velikosti absolutne vrednosti njihovega imaginarnega dela. Funkcija Li, ki se pojavlja v prvem členu, je funkcija (ordinatnega) logaritemskega integrala, ki je dan s Cauchyjevo glavno vrednostjo divergentnega integrala:
Člene funkcije Li(xρ), ki vsebujejo ničle funkcije ζ, je treba previdno definirati, ker ima funkcija Li vejišči v 0 in 1, in so definirani (za x > 1) z analitičnim nadaljevanjem kompleksne spremenljivke ρ v območju Re(ρ) > 0, kar pomeni, da jih je treba obravnavati kot Ei(ρ ln x). Tudi drugi členi odgovarjajo ničlam: prevladujoči člen funkcije Li(x) izhaja iz pola v s = 1, če se ga obravnava kot ničla multiplikativnosti −1, preostali manjši členi pa izhajajo iz trivialnih ničel. Za nekatere grafe vsot prvih členov te vrste glej Riesel; Göhl[22] ali Zagier.[23]
Ta formula pravi, da ničle Riemannove funkcije ζ nadzorujejo nihanja praštevil okrog njihovih »pričakovanih« leg. Riemann je vedel, da so netrivialne ničle funkcije ζ simetrično porazdeljene okrog premice s = 1/2 + it, prav tako je vedel, da morajo vse njene netrivialne ničle ležati v območju 0 ≤ Re(s) ≤ 1. Preveril je, da nekatere ničle ležijo na kritični premici z realnim delom enakim 1/2 in predlagal, da vse ležijo tam, kar je tudi domneva sama.
Posledice Riemannove domneve[uredi | uredi kodo]
Praktična raba Riemannove domneve vključuje več predlogov, ki veljajo, če je Riemannova domneva pravilna, in tiste, ki naj bi bili njej enakovredni.
Porazdelitev praštevil[uredi | uredi kodo]
Riemannova eksplicitna formula za število praštevil, manjših od danega števila, s členi vsote prek vseh ničel Riemannove funkcije ζ pravi, da velikost nihanj praštevil okrog njihovih pričakovanih leg nadzorujejo realni deli ničel funkcije ζ. Še posebej je člen napake v praštevilskem izreku tesno povezan z legami ničel. Na primer supremum realnih delov ničel je infimum takšnih števil β, da je napaka O(xβ).[24]
Von Koch je leta 1901 dokazal, da Riemannova domneva nakazuje »najbolj možno« mejo napake za praštevilski izrek.[25]
Točna različica von Kochovega rezultata po Schoenfeld (1976) pravi, da Riemannova domneva nakazuje:
Schoenfeld je leta 1976 tudi pokazal, da Riemannova domneva nakazuje:
kjer je ψ(x) druga funkcija Čebišova.
Rast aritmetičnih funkcij[uredi | uredi kodo]
Riemannova domneva nakazuje močne meje rasti mnogo drugih aritmetičnih funkcij poleg funkcije števila praštevil.
En zgled je Möbiusova funkcija μ. Izjava, da enačba:
velja za vsak s z realnim delom večjim od 1/2, kjer vsota na desni konvergira, je enakovredna Riemannovi domnevi. Od tod se lahko zaključi tudi, da, če je Mertensova funkcija definirana kot:
potem je trditev, da:
za vsak pozitiven ε, enakovredna Riemannovi domnevi.[b][c] Determinanta Redhefferjeve matrike reda n je enaka M(n), tako da se lahko Riemannova domneva izrazi kot pogoj za rast teh determinant. Riemannova domneva da precej ozko mejo rasti M, ker sta Odlyzko in te Riele leta 1985 dokazala nepravilnost malo močnejše Mertensove domneve:[26]
Riemannova domneva je enakovredna mnogim drugim domnevam o stopnji rasti drugih aritmetičnih funkcij poleg Möbiusove funkcije μ(n). Tipični zgled je Robinov izrek,[27] ki pravi, da, če je σ(n) funkcija vsote deliteljev, podana z:
potem velja:
če in samo če je Riemannova domneva pravilna. Tu je γ Euler-Mascheronijeva konstanta.
Drug primer je našel Jérôme Franel in ga razširil Landau.[28] Riemannova domneva je enakovredna več izjavam, ki kažejo, da so členi Fareyjevega zaporedja regularni. Ena takšna ekvivalenca je: če je Fn Fareyjevo zaporedje reda n in se začne z 1/n in konča z 1/1, potem je trditev, da za vse ε > 0:
enakovredna Riemannovi domnevi. Tukaj je:
število členov v Fareyjevem zaporedju reda n.
Za zgled iz teorije grup, če je g(n) Landauova funkcija podana z največjim redom elementov simetrične grupe Sn stopnje n, potem je Riemannova domneva enakovredna meji:[29]
za vse dovolj velike n.
Lindelöfova domneva in rast funkcije ζ[uredi | uredi kodo]
Riemannova domneva ima tudi več šibkejših posledic. Ena je Lindelöfova domneva[30] o stopnji rasti funkcije ζ na kritični premici iz leta 1908, ki pravi, da za vsak velja:
ko gre .
Iz Riemannove domneve izhajajo tudi precej ostre meje za stopnjo rasti funkcije ζ v drugih območjih kritičnega traku. Na primer:
tako da bi bila stopnja rasti ζ(1+it) in njenega inverza znana vse do faktorja 2.[19]
Domneva velikih praštevilskih vrzeli[uredi | uredi kodo]

Po praštevilskem izreku je povprečno vrzel med praštevilom in naslednjim praštevilom enaka:
Nekatere vrzeli pa so lahko veliko večje od povprečja. Cramér je dokazal, da je ob privzetku pravilnosti Riemannove domneve vsaka vrzel enaka:
To je primer, v katerem je tudi najboljša meja, ki se jo lahko dokaže s pravilnostjo Riemannove domneve, veliko šibkejša od tistega, kar se zdi resnično: Cramérjeva domneva pravi, da je vsaka vrzel med zaporednima prašteviloma enaka:
ki je sicer večja od povprečne vrzeli, vendar veliko manjša od meje, ki sledi iz Riemannove domneve. Numerični računi podpirajo Cramérjevo domnevo.[31]
Kriteriji enakovredni Riemannovi domnevi[uredi | uredi kodo]
Obstaja več kot sto izjav, ki so enakovredne Riemannovi domnevi, vendar do sedaj nobena ni vodila k napredku pri njenem dokazovanju (ali ovržbi). Sledijo nekateri tipični zgledi. Drugi vključujejo funkcijo števila deliteljev σ(n).
Rieszov kriterij je podal Marcel Riesz leta 1916.[32] Meja:
velja za vse , če in samo če je Riemannova domneva pravilna.
Nyman[33] je leta 1950 dokazal, da je Riemannova domneva pravilna, če in samo če je prostor funkcij oblike:
kjer je ρ(z) ulomljeni del z, 0 ≤ θν ≤ 1, in je:
gosta v Hilbertovem prostoru L2(0,1) kvadratnointegrabilnih funkcij v enotskem intervalu. Beurling[34] je leta 1955 to razširil in pokazal, da funkcija ζ nima ničel z realnim delom večjim od 1/p, če in samo če je ta funkcijski prostor gost v Lp(0,1).
Weilov kriterij je izjava, da je pozitivnost določene funkcije enakovredna Riemannovi domnevi. Bombieri in Lagarias sta pokazala, da sorodni Li-Keiperjev kriterij sledi iz Weilovega kriterija za posplošeno Riemannovo domnevo. Li-Keiperjev kriterij je izjava o pozitivnosti določenega zaporedja števil, ki je enakovredna Riemannovi domnevi.[35] Vse vrednosti členov zaporedja λn > 0 za vse pozitivne n. Števila , imenovana Li-Keiperjeve konstante[36] ali Keiper-Lijevi koeficienti,[37] se lahko izrazijo z netrivialnimi ničlami Riemannove funkcije ζ:
kjer vsota poteka po ρ, netrivialnih ničlah Riemannove funkcije ζ po vrsti , pa je polinom končno mnogo Steiltjesovih konstant.[38] To pogojno konvergentno vsoto je treba razumeti v smislu, ki se po navadi rabi v teoriji števil, tako da velja limita:
Speiser[39] je leta 1934 dokazal, da je Riemannova domneva enakovredna izjavi, da odvod funkcije ζ(s):
nima ničel v traku:
Da ima funkcija ζ le enostavne ničle na kritični premici, je enakovredno dejstvu, da njen odvod nima ničel na kritični premici.
Integralski kriteriji[uredi | uredi kodo]
Salem[40] je leta 1953 pokazal, da je Riemannova domneva pravilna, če in samo če integralska enačba:
nima netrivialnih omejenih rešitev za .
Volčkov[41][42] je leta 1995 podal ekvivalent Riemannove domneve v obliki eksaktnega integrala:
kjer je Euler-Mascheronijeva konstanta. Od tedaj so odkrili več enakovrednih formulacij Riemannove domneve z integrali logaritmov funkcije ζ. Posebna primera sta naslednja kriterija:
- Balazard-Saias-Yorov kriterij: Riemannova domneva je enakovredna integralu:
- kriterij Volčkova: Riemannova domneva je enakovredna integralu:
Elementarni kriteriji[uredi | uredi kodo]
Leta 1915 je Ramanudžan s privzetkom o pravilnosti Riemannove domneve dokazal, da velja (Robinova neenakost):
za dovolj velike n.[43] Leta 1984 je Robin dokazal, da neenakost velja za vse n ≥ 5041, če je Riemannova domneva pravilna (Robinov izrek).[27] Največje znano število, za katerega neenakost ne velja, je n = 5040. Če je Riemannova domneva pravilna, ne obstaja večja izjema. Če je Riemannova domneva nepravilna, je Robin pokazal, da obstaja neskončno mnogo vrednosti n, za katera neenakost ne velja. Znano je, da mora biti najmanjše takšno število n ≥ 5041 superobilno število.[44] Neenakost velja za velika liha in s kvadratom nedeljiva cela števila, Riemannova domneva pa je enakovredna neenakosti le za n deljive s peto potenco praštevila.[45]
Lagarias[46] je leta 2000 podal podoben elementarni kriterij. Riemannova domneva je enakovredna neenakostim:[47]
kjer je n-to harmonično število:
pa je funkcija vsote vseh deliteljev n. Enakost velja le za n = 1.
Robin je tudi brezpogojno dokazal, da velja neenakost:
Lagarias pa je dal še malo manjšo oceno:
Posledice posplošene Riemannove domneve[uredi | uredi kodo]
Več uporab rabi posplošeno Riemannovo domnevo za Dirichletovo L-vrsto ali funkcije ζ številskih obsegov namesto samo Riemannove domneve. Več osnovnih značilnosti Riemannove funkcije ζ se lahko preprosto posploši na vse Dirichletove L-vrste, tako da je smiselno, da bo metoda, ki dokaže Riemannovo domnevo za Riemannovo funkcijo ζ, delovala tudi za posplošeno Riemannovo domnevo za Dirichletove L-funkcije. Več rezultatom, ki so bili dokazani s pomočjo posplošene Riemannove domneve, so kasneje dali dokaze brez nje, čeprav so bili po navadi veliko težji. Več posledic na naslednjem seznamu je vzetih iz Conradovega dela.[48]
- Grönwall je leta 1913 pokazal, da posplošena Riemannova domneva nakazuje, da je Gaussov seznam imaginarnih kvadratnih številskih obsegov z razrednim številom 1 poln, čeprav so Baker, Stark in Heegner kasneje podali brezpogojne dokaze za to brez posplošene Riemannove domneve.
- Hardy in Littlewood sta leta 1917 pokazala, da iz posplošene Riemannove domneve izhaja domneva Čebišova:
- ki pravi, da so v nekem smislu praštevila 3 mod 4 običajnejša od praštevil 1 mod 4.
- Hardy in Littlewood sta leta 1923 pokazala, da iz posplošene Riemannove domneve izhaja šibka oblika Goldbachove domneve za liha števila: da je vsako dovolj veliko liho število vsota treh praštevil. Vinogradov pa je leta 1937 za to podal brezpogojni dokaz. Deshouillers, Effinger, te Riele in Zinovjev so leta 1997 pokazali, da iz posplošene Riemannove domneve izhaja, da je vsako liho število večje od 5 vsota treh praštevil.
- Čovla je leta 1934 pokazal, da iz posplošene Riemannove domneve izhaja, da je prvo praštevilo v aritmetičnem zaporedju a mod m je vsaj Km2log(m)2 za neko določeno konstanto K.
- Hooley je leta 1967 pokazal, da iz posplošene Riemannove domneve izhaja Artinova domneva o primitivnih korenih.
- Weinberger je leta 1973 pokazal, da obstaja vsaj še eno idonejsko število in, da iz posplošene Riemannove domneve izhaja, da je Eulerjev in Gaussov seznam 65-ih idonejskih števil poln.
- Weinberger[49] je leta 1973 pokazal, da iz posplošene Riemannove domneve za funkcije ζ vseh obsegov argebrskih števil izhaja, da je vsak obseg z razrednim številom 1 ali evklidski ali imaginarni kvadratni številski obseg diskriminant −19, −43, −67 ali −163.
- Miller je leta 1976 pokazal, da iz posplošene Riemannove domneve izhaja, da se lahko iz testa praštevilskosti v polinomskem času preskusi ali je število praštevilo s pomočjo Miller-Rabinovega testa. Agraval, Kajal in Saksena so leta 2002 dokazali ta rezultat brezpogojno s pomočjo testa praštevilskosti AKS.
- Odlyzko[50] je leta 1990 obravnaval, kako se lahko posplošeno Riemannovo domnevo uporabi za ostrejše ocene diskriminant in razrednega števila številskih obsegov.
- Ono in Soundararajan[51] sta leta 1997 pokazala, da iz posplošene Riemannove domneve izhaja, da obstaja točno 18 lihih celih števil, ki niso oblike Ramanudžanove integralske kvadratne forme x2 +y2 + 10z2: 3, 7, 21, 31, 33, 43, 67, 79, 87, 133, 217, 219, 223, 253, 307, 391, 679, 2719.
Izključena tretja možnost[uredi | uredi kodo]
Nekatere posledice Riemannove domneve so tudi posledice njene negacije, in so zato izreki. V svoji razpravi o izrekih Hecheja, Deuringa, Mordella in Heilbronna Ireland in Rosen pravita:[52]
»Tukaj je metoda dokaza resnično neverjetna. Če je posplošena Riemannova domneva pravilna, potem je izrek pravilen. Če je posplošena Riemannova domneva nepravilna, potem je izrek pravilen. Zato je izrek pravilen!!« (klicaja sta v izvirniku)
Treba je biti previden pri razumevanju kaj je mišljeno, da je posplošena Riemannova domneva nepravilna: treba je točno navesti kateri razred Dirichletovih vrst ima protiprimer.
Littlewoodov izrek[uredi | uredi kodo]
Izrek obravnava predznak napake v praštevilskem izreku. Izračunali so, da je funkcija števila praštevil π(x) < Li(x) za vse x ≤ 1023. Ni znana nobena vrednost x, za katero bi veljalo π(x) > Li(x).
Littlewood je leta 1914 dokazal, da obstajajo poljubno velike vrednosti x za katere velja:
in, da obstajajo poljubno velike vrednosti x za katere velja:
Tako razlika med funkcijama π(x) − Li(x) spremeni predznak neskončno mnogokrat. Ogromno Skewesovo število je ocena vrednosti x, ki bi odgovarjala prvi spremembi predznaka.
Littlewoodov dokaz je razdeljen na dva primera: v prvem Riemannova domneva velja za nepravilno (približno pol strani v Inghamovem delu[53]), v drugem pa naj bi bila pravilna (več ducatov strani).
Gaussova domneva o razrednem številu[uredi | uredi kodo]
To je domneva (prvič navedena v članku 303 Gaussovega dela Disquisitiones Arithmeticae), da obstaja le končno število imaginarnih kvadratnih obsegov z danim razrednim številom. Ena pot dokaza bi bila, da se pokaže, da, ko gre diskriminanta D → −∞, gre razredno število h(D) → ∞.
Naslednji niz izrekov, ki vsebujejo Riemannovo domnevo, je opisan v delu Irelanda in Rosena:[54]
Izrek (Hecke; 1918). Naj bo D < 0 diskriminanta imaginarnega kvadratnega številskega obsega K. Privzame se posplošena Riemannova domneva za L-funkcije vseh imaginarnih kvadratnih Dirichletovih karakterjev. Potem obstaja takšna konstanta C, da velja:
Izrek (Deuring; 1933). Če je Riemannova domneva nepravilna, potem je h(D) > 1, če je |D| dovolj velika.
Izrek (Mordell; 1934). Če je Riemannova domneva nepravilna, potem gre h(D) → ∞, ko gre D → −∞.
Izrek (Heilbronn; 1934). Če je posplošena Riemannova domneva nepravilna za L-funkcijo kakšnega imaginarnega kvadratnega Dirichletovega karakterja, potem gre h(D) → ∞, ko gre D → −∞. [d]
Siegel je leta 1935 podal močnejši rezultat brez kakršnekoli rabe Riemannove ali posplošene Riemannove domneve.
Rast Eulerjeve funkcije φ[uredi | uredi kodo]
Nicolas je leta 1983 dokazal, da velja:[55]
za neskončno mnogo n, kjer je φ(n) Eulerjeva funkcija φ.
Ribenboim je pripomnil, da:
»je metoda dokaza zanimiva v smislu, da neenakost velja pod privzetkom pravilnosti Riemannove domneve, in drugič pod nasprotnim privzetkom.«
Posplošitve in analogoni Riemannove domneve[uredi | uredi kodo]
Dirichletova L-vrsta in drugi obsegi[uredi | uredi kodo]
Riemannova domneva se lahko posploši z zamenjavo Riemannove funkcije ζ s formalno podobnimi, vendar veliko splošnejšimi globalnimi L-funkcijami. V tem širšem pogledu se pričakuje, da imajo netrivialne ničle globalnih L-funkcij realni del enak 1/2. Te domneve namesto klasične Riemannove domneve le za Riemannovo funkcijo ζ kažejo resnično pomembnost Riemannove domneve v matematiki.
Posplošena Riemannova domneva razširi Riemannovo domnevo na vse Dirichletove L-funkcije. Iz nje še posebej izhaja, da Sieglove ničle (ničle L-funkcij med 1/2 in 1) ne obstajajo.
Razširjena Riemannova domenva razširi Riemannovo domnevo za vse Dedekindove funkcije ζ obsegov algebrskih števil. Razširjena Riemannova domneva za abelovsko razširitev racionalnih števil je enakovredna posplošeni Riemannovi domnevi. Tudi Riemannovo domnevo se lahko razširi na L-funkcije Heckejevih karakterjev obsegov.
Velika Riemannova domneva razširi Riemannovo domnevo na vse avtomorfne funkcije ζ, kot so Mellinove transformacije Heckejevih lastnih form.
Funkcijski obsegi in funkcije ζ varietet končnih obsegov[uredi | uredi kodo]
Artin[56] je leta 1924 vpeljal globalne funkcije ζ (kvadratnih) funkcijskih obsegov in zanje postavil analogon Riemannove domneve. Dokazal ga je Hasse za primer roda 1, v splošnem pa Weil leta 1948.[57] Dejstvo, da je absolutna vrednost Gaussove vsote kvadratnega karakterja končnega obsega velikosti q (kjer je q lih) enaka:
je dejansko vrsta Riemannove domneve v okvirju funkcijskega obsega. To je vodilo Weila,[58] da je leta 1949 domneval podobno izjavo za vse algebrske varietete; Weilove domneve je dokazal Deligne leta 1974 in 1980.[59][60]
Aritmetična funkcija ζ aritmetičnih shem in njihovi L-faktorji[uredi | uredi kodo]
Aritmetične funkcije ζ posplošijo Riemannovo in Dedekindove funkcije ζ kakor tudi funkcije ζ varietet čez končne obsege na vsako aritmetično shemo ali shemo končnega tipa čez cela števila. Aritmetična funkcija ζ regularno povezane enakorazsežne aritmetične sheme s Kroneckerjevo razsežnostjo n se lahko faktorizira v produkt ustrezno definiranih L-faktorjev in pomožnega faktorja.[61] Če se privzame funkcijska enačba in meromorfno nadaljevanje, posplošena Riemannova domneva za L-faktor pravi, da njegove ničle znotraj kritičnega traku ležijo na osrednji premici. Ustrezno temu posplošena Riemannova domneva za aritmetično funkcijo ζ regularno povezane enakorazsežne aritmetične sheme pravi, da njene ničle znotraj kritičnega traku ležijo na navpičnih premicah in njeni poli znotraj kritičnega traku na navpičnih premicah . To je znano za sheme v pozitivni karakteristiki in izhaja iz Deligneovega rezultata,[59][60], vendar ostaja popolnoma neznano za ničelno karakteristiko.
Selbergove funkcije ζ[uredi | uredi kodo]
Selberg[62] je leta 1956 vpeljal Selbergovo funkcijo ζ Riemannove ploskve. Te so podobne Riemannovi funkciji ζ: imajo funkcijsko enačbo in neskončni produkt podoben Eulerjevemu produktu, vendar ta poteka čez sklenjene geodetke in ne čez praštevila. Selbergova sledna formula je analogon za te funkcije eksplicitnih formul v teoriji praštevil. Selberg je dokazal, da za Selbergovo funkcijo ζ velja analogon Riemannove domneve, z imaginarnimi deli njihovih ničel, ki so povezane z lastnimi vrednostmi Laplaceovega operatorja Riemannove ploskve.
Iharove funkcije ζ[uredi | uredi kodo]
Iharova funkcija ζ končnega grafa je analogon Selbergove funkcije ζ, ki jo je prvič uvedel Ihara v kontekstu diskretnih podgrup p-adične specialne linearne grupe dva krat dva. Regularni končni graf je Ramanudžanov graf, matematični model učinkovitih komunikacijskih mrež, če in samo če za Iharovo funkcijo ζ velja analogon Riemannove domneve, kot je pokazal Sunada.
Montgomeryjeva domneva o parni korelaciji[uredi | uredi kodo]
Montgomery je leta 1973[63] predlagal domnevo o parni korelaciji, da je lahko korelacijska funkcija (ustrezno normaliziranih) ničel funkcije ζ enaka kot tiste lastnih vrednosti slučajne hermitske matrike. Odlyzko[64] je leta 1987 pokazal, da to podpirajo numerični izračuni velikega obsega teh korelacijskih funkcij.
Montgomery je (s privzetkom Riemannove domneve) pokazal, da je vsaj 2/3 od vseh ničel enostavnih. Povezana domneva je, da so vse ničle funkcije ζ enostavne (oziroma bolj splošno nimajo netrivialnih celoštevilskih linearnih relacij med svojimi imaginarnimi deli). Dedekindove funkcje ζ obsegov algebrskih števil, ki posplošijo Riemannovo funkcijo ζ, imajo običajno mnogokratne kompleksne ničle.[65] To je zato, ker se Dedekindove funkcije ζ faktorizirajo kot produkt potenc Artinovih L-funkcij, tako da Artinove L-funkcije včasih dajo mnogokratne ničle Dedekindovih funkcij ζ. Drug primer funkcij ζ z mnogokratnimi ničlami so L-funkcije kakšnih eliptičnih krivulj: te imajo lahko mnogokratne ničle v realni točki svoje kritične premice; Birch-Swinnerton-Dyerjeva domneva predvideva, da je multiplikativnost te ničle rang eliptične krivulje.
Druge funkcije ζ[uredi | uredi kodo]
Obstaja več drugih primerov funkcij ζ z analogoni Riemannove domneve, od katerih so nekateri že dokazani. Gossove funkcije ζ funkcijskih obsegov imajo Riemannovo domnevo, ki jo je dokazal Sheats[66] leta 1998. Glavna domneva Ivasavove teorije, ki sta jo dokazala Mazur in Wiles za ciklotomske obsege, in Wiles za totalno realne obsege, istoveti ničle p-adične L-funkcije z lastnimi vrednostmi operatorja, zato se jo lahko obravnava kot analogon Hilbert-Pólyeve domneve za p-adične L-funkcije.[67]
Poskusi dokaza Riemannove domneve[uredi | uredi kodo]
Več matematikov je reševalo Riemannovo domnevo, vendar nobenega njihovega poskusa še niso sprejeli za pravilno rešitev. Watkins[68] navaja nekatere nepravilne rešitve, več pa jih pogosto najavijo.
Teorija operatorjev[uredi | uredi kodo]
Hilbert in Pólya sta predlagala eno pot za rešitev Riemannove domneve, kjer bi se našel sebiadjungirani operator, iz katerega obstoja bi izhajala izjava o realnih delih funkcije ζ(s), če bi se uporabil kriterij na realne lastne vrednosti. Ena podpora te zamisli izhaja iz več analogonov Riemannove funkcije ζ, katere ničle odgovarjajo lastnim vrednostim kakšnega operatorja: ničle funkcije ζ varietete čez končni obseg odgovarjajo lastnim vrednostim Frobeniusovega elementa na grupi kohomologije étale, ničle Selbergove funkcije ζ so lastne vrednosti Laplaceovega operatoraja Riemannove ploskve, ničle p-adične funkcije ζ pa odgovarjajo lastnim vrednostim Galoisove akcije na grupah idealnih razredov.
Odlyzko[64] je leta 1987 pokazal, da porazdelitev ničel Riemannove funkcije ζ deli nekatere statistične značilnosti z lastnimi vrednostmi slučajnih matrik, izvedenih iz gaussovskega enotskega ansambla. To da nekaj podpore Hilbert-Pólyevi domnevi.
Berry in Keating sta leta 1999 domnevala, da obstaja neka neznana kvantizacija klasične Hamiltonove funkcije H = xp, da velja:
in še močneje, da ničle Riemannove funkcije ζ sovpadajo s spektrom operatorja . To je v nasprotju s kanonično kvantizacijo, kar vodi do Heisenbergovega načela nedoločenosti in naravnim številom kot spektru kvantnega harmoničnega oscilatorja. Odločilna točka je, da mora biti Hamiltonova funkcija sebiadjungirani operator, da bo kvantizacija uresničitev Hilbert-Pólyevega programa. V povezavi s tem kvantnomehanskim problemom sta Berry in Connes predlagala, da je inverz potenciala Hamiltonove funkcije povezan s polodvodom funkcije:
potem v Berry-Connesovem pristopu velja:[69]
To vodi do Hamiltonove funkcije, katere lastne vrednosti so kvadrat imaginarnega dela ničel Riemannove funkcije ζ in tudi funkcijska determinanta tega Hamiltonovega operatorja je samo Riemanova funkcija ξ. Dejansko bo Riemannova funkcija ξ sorazmerna s funkcijsko determinanto (Hadamardov produkt):
kakor so dokazali Connes in drugi, v tem pristopu velja:
Analogija z Riemannovo domnevo čez končne obsege nakazuje, da bi Hilbertov prostor, ki vsebuje lastne vektorje odgovarjajoče ničlam, lahko bil neke vrste prva kohomološka grupa spektra Spec(Z) celih števil. Deninger[70] je leta 1998 opisal nekatere poskuse iskanja takšne teorije kohomologije.[71]
Zagier[72] je leta 1981 skonstruiral naravni prostor invariantnih funkcij na zgornji polravnini, ki ima lastne vrednosti pod Laplaceovim operatorjem, ki odgovarjajo ničlam Riemannove funkcije ζ. Pripomnil je, da bi se z malo verjetnostjo lahko pokazal obstoj ustreznega pozitivno definitnega notranjega produkta na tem prostoru, od koder bi izhajala Riemannova domneva. Cartier[73] je leta 1982 obravnaval povezan soroden primer, kjer je zaradi nenavadnega hrošča računalniški program navedel ničle Riemannove funkcije ζ kot lastne vrednosti istega Laplaceovega operatorja.
Schumayer in Hutchinson[74] sta leta 2011 podala pregled poskusov konstrukcije ustreznega fizikalnega modela povezanega z Riemannovo funkcijo ζ.
Lee-Yangov izrek[uredi | uredi kodo]
Lee-Yangov izrek pravi, da vse ničle določenih particijskih funkcij v statistični mehaniki ležijo na »kritični premici« z realnim delom enakim 0. To je vodilo do razglabljanja o povezavi z Riemannovo domnevo.[75]
Turánov rezulat[uredi | uredi kodo]
Turán[76] je leta 1948 pokazal, da če funkcije:
nimajo ničel, ko je realni del s večji od 1, potem velja:
kjer je λ(n) Liouvillova funkcija podana za (−1)r, če ima n r prafaktorjev. Pokazal je, da bi iz tega po vrsti izhajala pravilnost Riemannove domneve. Vendar je Haselgrove[77] leta 1958 dokazal, da je T(x) negativna za neskončno mnogo x (in tudi ovrgel tesno povezano Pólyevo domnevo), Peter Borwein, Ferguson in Mossinghoff[78] pa so leta 2008 pokazali, da je najmanjši takšen x enak 72 185 376 951 205. Spira[79] je leta 1968 z numeričnim izračunom pokazal, da ima zgornja končna Dirichletova vrsta nad N = 19 ničlo z realnim delom večjim od 1. Turán je tudi pokazal, da bi iz nekoliko šibkejšega privzetka, neobstoj ničel z realnim delom večjim od za velike N v zgornji končni Dirichletovi vrsti, tudi izhajala Riemannova domneva. Vendar je Montgomery[80] leta 1983 pokazal, da imajo za vse dovolj velike N te vrste ničle z realnim delom večjim od . Tako je Turánov rezultat prazno pravilen in ga ni moč uporabiti za dokaz Riemannove domneve.
Nekomutativna geometrija[uredi | uredi kodo]
Connes[69][81] je leta 1999 in 2000 opisal povezavo med Riemannovo domnevo in nekomutativno geometrijo. Pokazal je, da bi iz ustreznega analogona Selbergove sledne formule za akcijo idelske razredne grupe na adelski razredni prostor izhajala Riemannova domneva. Nekaj od teh zamisli izčrpno navaja Lapidus.[82]
Hilbertovi prostori celih funkcij[uredi | uredi kodo]
De Branges[83] je leta 1992 pokazal, da bi Riemannova domneva izhajala iz kriterija pozitivnosti na določenem Hilbertovem prostoru celih funkcij. Vendar sta Conrey in Li[84] leta 2000 pokazala, da potrebni kriteriji pozitivnosti ne veljajo.
Kvazikristali[uredi | uredi kodo]
Iz Riemannove domneve izhaja, da ničle funkcije ζ tvorijo kvazikristal, kar pomeni porazdelitev nezvezne opore, katere Fourierova transformacija ima tudi nezvezno oporo. Dyson[85] je leta 2009 predlagal poskus dokaza Riemannove domneve s klasifikacijo, oziroma vsaj z raziskovanjem 1-razsežnih kvazikristalov, ki imajo dosti bogatejšo vsebino od na primer trirazsežnih. Nekateri menijo, da njegova definicija kvazikristalov ni ustrezna.
Aritmetične funkcije ζ modelov eliptičnih krivulj številskih obsegov[uredi | uredi kodo]
Če se prestopi iz geometrične razsežnosti 1, na primer obsega algebrskih števil, na geometrično razsežnost 2, na primer model eliptične krivulje čez številski obseg, dvorazsežni del posplošene Riemannove domneve za aritmetično funkcijo ζ modela obravnava pole funkcije ζ. V razsežnosti 1 raziskovanje integrala ζ v tateovi disertaciji ne vodi do novih pomembnih informacij o Riemannovi domnevi. V nasprotju s tem, Fesenkovo delo v razsežnosti 2 o dvorazsežni posplošitvi Tateove disertacije vsebuje integralsko reprezentacijo integrala ζ, ki je tesno povezan s funkcijo ζ. V teh novih razmerah, ki v razsežnosti 1 niso možne, se lahko poli funkcije ζ raziskujejo prek integrala ζ in priključenih adelskih grup. Sorodna Fesenkova domneva[86] iz leta 2010 o pozitivnosti četrtega odvoda mejne funkcije povezane z integralom ζ bistveno nakazuje polov del posplošene Riemannove domneve. Suzuki [87] je leta 2011 dokazal, da zadnje skupaj z nekaterimi tehničnimi privzetki nakazuje Fesenkovo domnevo.
Mnogokratne funkcije ζ[uredi | uredi kodo]
Delignejev dokaz Riemannove domneve čez končne obsege je uporabil funkcije ζ produktov varietet, katerih ničle in poli odgovarjajo vsotam ničel in polov izvirne funkcije ζ, da bi se omejili realni deli ničel izvirne funkcije ζ. Po analogiji je Kurokava[88] leta 1992 uvedel mnogokratne funkcije ζ, katerih ničle in poli odgovarjajo vsotam ničel in polov Riemannove funkcije ζ. Da bi vrsta konvergirala, je omejil vsote ničel ali polov z nenegativnim imaginarnim delom. Do sedaj znane meje ničel ali polov mnogokratnih funkcij ζ niso dovolj močne, da bi dale ocene za ničle Riemannove funkcije ζ.
Značilnosti ničel in njihova lega[uredi | uredi kodo]
Število ničel[uredi | uredi kodo]
Funkcijska enačba kombinirana z načelom argumenta nakazuje, da je število ničel funkcije ζ z imaginarnim delom med 0 in T dano z izrazom:
za s=1/2+iT, kjer je argument definiran s stalnim spreminjanjem vzdolž premice z Im(s)=T, z začetnim argumentom 0 v ∞+iT. To je vsota velikega, vendar dobro znanega člena:
in manjšega, vendar skrivnostnega člena:
Tako je gostota ničel z imaginarnim delom blizu T približno enaka log(T)/2π, funkcija S pa opiše majhne odklone od tega. Funkcija S(t) skače po 1 v vsaki ničli funkcije ζ, in za t ≥ 8 monotono pada med ničlami z odvodom blizu −log t.
Karacuba je leta 1996 dokazal, da vsak interval (T, T+H] za vsebuje vsaj:
točk, kjer funkcija S(t) spremeni predznak.
Selberg[89] je leta 1946 pokazal, da so povprečni momenti sodih potenc funkcije S dani z:
To nakazuje, da je S(T)/(log log T)1/2 podobno gaussovski slučajni spremenljivki s povprečjem 0 in varianco 2π2. To dejstvo je dokazal Ghosh leta 1983.[90] Še posebej je |S(T)| po navadi približno okrog (log log T)1/2, občasno pa je veliko večja. Točna stopnja rasti S(T) ni znana. Ne obstaja brezpogojna izboljšava Riemannove izvirne meje S(T) = O(log T), čeprav iz Riemannove domneve izhaja rahlo manjša meja S(T) = O(log T/log log T).[19] Prava stopnja velikosti je lahko malo manjša od tega, ker imajo slučajne funkcije z enako porazdelitvijo kot S(T) rast reda približno log(T)1/2. V drugi smeri ne more biti premajhna: Selberg[89] je leta 1946 pokazal, da S(T) ≠ o((log T)1/3/(log log T)7/3), in s privzetkom pravilnosti Riemannove domneve je Montgomery pokazal, da S(T) ≠ o((log T)1/2/(log log T)1/2).
Numerični izračuni potrjujejo, da S raste zelo počasi: |S(T)| < 1 za T < 280, |S(T)| < 2 za T < 6 800 000, največja vrednost |S(T)| najdena do sedaj je veliko večja kot 3.[91]
Iz Riemannove ocene S(T) = O(log T) izhaja, da so vrzeli med ničlami omejene. Littlewood je to malenkost izboljšal in pokazal, da vrzeli med njihovimi imaginarnimi deli težijo k 0.
Hadamardov in La Vallée Poussinov izrek[uredi | uredi kodo]
Hadamard[92] in La Vallée Poussin[93] sta leta 1896 neodvisno dokazala, da nobena ničla ne more ležati na premici Re(s) = 1. Skupaj s funkcijsko enačbo in dejstvom, da ne obstaja nobena ničla z realnim delom večjim od 1, je to pokazalo, da morajo vse netrivialne ničle ležati v notranjosti kritičnega traku 0 < Re(s) < 1. To je bil odločilni korak v njihovih prvih dokazih praštevilskega izreka.
Oba izvirna dokaza, da funkcija ζ nima ničel z realnim delom enakim 1, sta podobna, in sta odvisna od razkritja, da, če se izniči, potem je edina, kar ni možno. En način za to je z uporabo neenakosti:
za σ > 1, t realno število in iskanje limite, ko gre σ → 1. Ta neenakost sledi, če se vzame realni del logaritma Eulerjevega produkta:
kjer vsota poteka po vseh praštevilskih potencah pn, tako da je:
kar je vsaj enako 1, ker so vsi členi v vsoti pozitivni, zaradi neenakosti:
Območja brez ničel[uredi | uredi kodo]

La Vallée Poussin[94] je med letoma 1899 in 1900 dokazal, da če je ničla Riemannove funkcije ζ, potem velja 1 − σ ≥ Clog(t) za kakšno pozitivno konstanto C. Z drugimi besedami ničle ne morejo biti preblizu premici σ = 1: tam obstaja območje brez ničel blizu te premice. To območje brez ničel je več avtorjev povečalo z metodami, kot je na primer izrek Vinogradova o srednji vrednosti. Ford[95] je leta 2002 podal različico z eksplicitnimi številskimi konstantami: , kadar je |t | ≥ 3 in:
Ničle na kritični premici[uredi | uredi kodo]
Hardy[96] in Littlewood[97] sta leta 1914 in 1921 pokazala, da obstaja neskončno mnogo ničel na kritični premici z upoštevanjem momentov določenih funkcij povezanih s funkcijo ζ. Selberg[98] je leta 1942 dokazal, da vsaj (majhen) pozitiven delež ničel leži na premici. Levinson[99] je leta 1974 izboljšal to na eno tretjino ničel s povezavo ničel funkcije ζ s tistimi iz odvoda. Conrey[100] je leta 1989 to še izboljšal na dve petini ničel.
Večina ničel leži blizu kritične premice. Bohr in Landau[101] sta leta 1914 točneje pokazala, da za vsak pozitiven ε, vse ničle, razen neskončno majhnega deleža ničel, leži znotraj razdalje ε od kritične premice. Ivić[20] je leta 1985 dal več točnejših različic tega rezultata, in jih imenoval ocene z ničelno gostoto. Te omejujejo ničle v območjih z imaginarnim delom največ T in realnim delom vsaj 1/2 + ε.
Hardy-Littlewoodove domneve[uredi | uredi kodo]
Hardy je leta 1914 dokazal, da ima neskončno mnogo realnih ničel.
Naj je N(T) celotno število realnih ničel, celotno število ničel lihega reda funkcije:
ki ležijo na intervalu (0, T].
Naslednji dve domnevi Hardyja in Littlewooda o razdalji med realnimi ničlami funkcije in o gostoti ničel funkcije na intervalih (T, T+H] za dovolj velike T > 0, in z najmanjšo možno vrednostjo a > 0, kjer je ε > 0 poljubno majhno število, sta odprli nove smeri pri raziskovanju Riemannove funkcije ζ:
- 1. za poljubni ε > 0 obstaja takšen , da za in interval vsebuje ničlo lihega reda funkcije .
- 2. za poljubni ε > 0 obstajata takšna in c = c(ε) > 0, da za in velja neenakost .
Selbergova domneva[uredi | uredi kodo]
- Ta razdelek ni o Selbergovi domnevi o 1/4 ampak o Selbergovi domnevi o funkciji ζ.
Selberg[98] je leta 1942 raziskal Hardy-Littlewoodov problem 2 in dokazal, da za poljubni obstajata takšna in , da bo za in veljala neenakost . Selberg je domneval, da se to lahko zoži na . Karacuba[102][103][104] je med letoma 1984 in 1985 dokazal, da za fiksni , za katerega velja pogoj , dovolj veliki in , , interval vsebuje vsaj realnih ničel Riemannove funkcije in tako potrdil Selbergovo domnevo. Selbergove in Karacubove ocene se ne dajo izboljšati glede na stopnjo rasti, ko gre .
Karacuba[105] je leta 1992 dokazal, da analogon Selbergove domneve velja za skoraj vse intervale , , kjer je poljubno majhno fiksno pozitivno število. Karacubova metoda dovoljuje raziskavo ničel Riemannove funkcije ζ na »superkratkih« intervalih kritične premice, to je na intervalih , dolžina , ki se povečuje počasneje kot katerakoli, četudi poljubno majhna stopnja <maath>T\, </math>. Dokazal je še posebej, da za poljuno število , , za katerega veljajo pogoji , skoraj vsi intervali za vsebujejo vsaj ničel funkcije . Ta ocena je zelo blizu tisti, ki izhaja iz Riemannove domneve.
Numerični izračuni[uredi | uredi kodo]
Funkcija:
ima enake ničle kot funkcija ζ na kritičnem traku, in je realna na kritični premici zradi funkcijske enačbe, tako da se lahko dokaže obstoj ničel točno na realni premici med dvema točkama z numeričnim preverjanjem, ali ima funkcija nasprotna predznaka v teh točkah. Po navadi se zapiše:
kjer sta Hardyjeva funkcija Z in Riemann-Sieglova funkcija θ posebno definirani s tem in s pogojem, da sta gladki realni funkciji z vrednostjo . Z iskanjem več intervalov, kjer funkcija Z spremeni predznak, se lahko pokaže, da obstaja mnogo ničel na kritični premici. Da se preveri Riemannova domneva do danega imaginarnega dela ničel, je treba preveriti tudi, da ne obstajajo druge ničle zunaj premice v tem območju. To se lahko doseže z računanjem celotnega števila ničel v območju in s preverjanjem, ali je enako kot število ničel najdenih na premici. Na ta način se lahko preveri Riemannova domneva do poljubne vrednosti (s tem, da se zagotovi, da so vse ničle funkcije ζ v tem območju enostavne in na kritični premici).
Nekateri izračuni ničel funkcije ζ so navedeni v spodnji razpredelnici. Do sedaj vse preverjene ničle ležijo na kritični premici in so enostavne.[e] Za razpredelnice ničel glej delo Haselrovea in Millerja[106] ali delo Odlyzka.[107]
| leto | število ničel | avtor |
|---|---|---|
| 1859? | 3 | B. Riemann je uporabil Riemann-Sieglovo formulo (neobjavljeno, vendar navedeno v Siglovem delu[108]). |
| 1903 | 15 | J. P. Gram[109] je uporabil Euler-Maclaurinovo vsoto in odkril Gramov zakon. Pokazal je, da vseh 10 ničel z imaginarnim delom največ 50 leži na kritični premici z realnim delom enakim 1/2 z računanjem vsote inverza 10-ih potenc korenov, ki jih je našel. |
| 1914 | 79 (γn ≤ 200) | R. J. Backlund[110] je uvedel boljšo metodo za preverjanje vseh ničel do dane točke ali ležijo na premici z raziskovanjem argumenta S(T) funkcije ζ. |
| 1925 | 138 (γn ≤ 300) | J. I. Hutchinson[111] je našel prvo neskladje z Gramovim zakonom, v Gramovi točki g126. |
| 1935 | 195 | E. C. Titchmarsh[112] je uporabil nedavno ponovno odkrito Riemann-Sieglovo formulo, ki je veliko hitrejša od Euler-Maclaurinove vsote. Potrebno je približno O(T3/2+ε) korakov za preverbo ničel z imaginarnim delom manjšim od T, Euler-Maclaurinova metoda pa zahteva približno O(T2+ε) korakov. |
| 1936 | 1041 | E. C. Titchmarsh[113] in L. J. Comrie sta bila zadnja, ki sta iskala ničle na roke. |
| 1953 | 1104 | A. M. Turing[114] je našel učinkovitejši način preverjanja, da so vse ničle do neke točke upoštevane z ničlami na premici, tako da se preveri ali ima funkcija Z pravilni predznak v več zaporednih Gramovih točkah in z uporabo dejstva, da je srednja vrednost S(T) enaka 0. To ne zahteva skoraj nobenega dodatnega dela, ker je predznak funkcije Z v Gramovih točkah že znan iz iskanja ničel. Ta metoda se običajno še vedno uporablja. To je bila prva raba digitalnega računalnika za izračun ničel. |
| 1956 | 15 000 | D. H. Lehmer[115] je odkril nekaj primerov, kjer ima funkcija ζ ničle, ki ležijo »komaj« na premici: dve ničli funkcije ζ sta tako blizu skupaj, da je izredno težko najti spremembo predznaka med njima. To se imenuje »Lehmerjev par« in se prvič pojavi pri ničlah z imaginarnima deloma 7005,063 in 7005,101, ki se razlikujeta le za 0,04, medtem ko je povprečna vrzel med drugimi ničlami blizu te točke približno enaka 1. |
| 1956 | 25 000 | D. H. Lehmer |
| 1958 | 35 337 | N. A. Meller |
| 1966 | 250 000 | R. S. Lehman |
| 1968 | 3 500 000 | Rosser, Yohe in Schoenfeld[116] so navedli Rosserjevo pravilo (opisano spodaj). |
| 1977 | 40 000 000 | R. P. Brent |
| 1979 | 81 000 001 | R. P. Brent |
| 1982 | 200 000 001 | R. P. Brent, J. van de Lune, H. J. J. te Riele, D. T. Winter |
| 1983 | 300 000 001 | J. van de Lune, H. J. J. te Riele |
| 1986 | 1 500 000 001 | J. van de Lune, H. J. J. te Riele in D. T. Winter[117] so podali nekaj statističnih podatkov o ničlah in izdelali več grafov funkcije Z na mestih kjer se neobičajno obnaša. |
| 1987 | nekaj z veliko višino (~1012) | A. M. Odlyzko[64] je izračunal majhno število ničel z veliko večjo višino, približno 1012, do visoke točnosti za preverbo Montgomeryjeve domneve o parni korelaciji. |
| 1992 | nekaj z veliko višino (~1020) | A. M. Odlyzko[118] je izračunal 175 milijonov ničel z višinami približno 1020 in nekaj z višinami približno 2×1020, in podal obširno razpravo o rezultatih. |
| 1998 | 10000 z veliko višino (~1021) | A. M. Odlyzko[119] je izračunal nekaj ničel z višino približno 1021 |
| 2001 | 10 000 000 000 | J. van de Lune (neobjavljeno) |
| 2004 | 900 000 000 000 | S. Wedeniwski (distribuirano računanje ZetaGrid) |
| 2004 | 10 000 000 000 000 in nekaj z velikimi višinami (do ~1024) | X. Gourdon[120] in Patrick Demichel sta uporabila Odlyzko-Schönhageov algoritem. Preverila sta tudi dve milijardi ničel z višinami približno 1013, 1014, ... , 1024. |
Gramove točke[uredi | uredi kodo]
Gramova točka je točka na kritični premici 1/2 + it, kjer je funkcija ζ realna in neničelna. S pomočjo izraza za funkcijo ζ na kritični premici ζ(1/2 + it) = Z(t)e − iθ(t), kjer je Hardyjeva funkcija Z realna za realni t, θ pa je Riemann-Sieglova funkcija θ, se vidi, da je funkcija ζ realna, ko je sin(θ(t)) = 0. Iz tega izhaja, da je θ(t) celoštevilski mnogokratnik števila π, kar omogoča, da se lega Gramovih točk izračuna dokaj preprosto z inverzom formule za θ. Po navadi so označene z gn za n = 0, 1, ..., kjer je gn edina rešitev θ(t) = nπ.
Gram je opazil, da je bila med dvema Gramovima točkama pogosto točno ena ničla funkcije ζ. Hutchinson je poimenoval to opažanje Gramov zakon. Obstaja več drugih tesno povezanih izjav, ki se včasih tudi imenujejo Gramov zakon, na primer:
- (−1)nZ(gn) je po navadi pozitiven, ali
- funkcija Z(t) ima po navadi nasprotni predznak v naslednjih Gramovih točkah.
Imaginarni deli γn prvih ničel (modro) in prvih nekaj Gramovih točk gn podaja naslednja razpredelnica
| g−1 | γ1 | g0 | γ2 | g1 | γ3 | g2 | γ4 | g3 | γ5 | g4 | γ6 | g5 | ||
| 0,000 | 3,436 | 9,667 | 14,135 | 17,846 | 21,022 | 23,170 | 25,011 | 27,670 | 30,425 | 31,718 | 32,935 | 35,467 | 37,586 | 38,999 |

Prvo neskladje Gramovega zakona se pojavi pri 127-i ničli in Gramovi točki g126, ki sta v »nepravilnem« vrstnem redu.
| g124 | γ126 | g125 | g126 | γ127 | γ128 | g127 | γ129 | g128 |
|---|---|---|---|---|---|---|---|---|
| 279,148 | 279,229 | 280,802 | 282,455 | 282,465 | 283,211 | 284,104 | 284,836 | 285,752 |
Gramova točka t je dobra, če je funkcija ζ pozitivna v 1/2 + it. Indeksi »slabih« Gramovih točk, kjer ima funkcija Z »napačni« predznak, so: 126, 134, 195, 211 ... (OEIS A114856). Gramov blok je interval omejen z dvema dobrima Gramovima točkama, tako da so vse Gramove točke med njimi slabe. Izboljšava Gramovega zakona, imenovana Rosserjevo pravilo[116] pravi, da je v Gramovih blokih pogosto pričakovano število ničel (enako kot število Gramovih intervalov), četudi v katerem od posameznih Gramovih intervalov v bloku mogoče ni točno ene ničle. Interval omejen s točkama g125 in g127 je na primer Gramov blok, ki vsebuje edino slabo Gramovo točko g126, in vsebuje pričakovano število dveh ničel, čeprav v nobenem od njegovih dveh Gramovih intervalov ni posamezne ničle. Rosser je s sodelavci preveril izjeme v Rosserjevem pravilu v prvih treh milijonih ničel, čeprav obstaja neskončno mnogo izjem Rosserjevega pravila na celi funkciji ζ.
Gramov zakon in Rosserjevo pravilo oba pravita, da v nekem smislu ničle ne zaidejo predaleč od svojih pričakovanih leg. Razdaljo ničle od njene pričakovane lege podaja funkcija S definirana zgoraj. Ta raste izredno počasi: njena povprečna vrednost je reda (log log T)1/2 in doseže vrednost 2 šele za T približno 1024. To pomeni, da obe pravili veljata večino časa za majhne T, pogosto pa ne veljata. Trudgian[121] je leta 2011 res pokazal, da Gramov zakon in Rosserjevo pravilo ne veljata v pozitivnem deležu primerov. Pričakuje se, da bosta v približno 73 % primerov posamezno ničlo obkrožali dve zaporedni Gramovi točki, v 14 % primerov nobena, v 13 % primerov pa sta sčasoma dve ničli v takšnem Gramovem intervalu.
Argumenti za Riemannovo domnevo in proti njej[uredi | uredi kodo]
Matematični članki o Riemannovi domnevi so o njeni pravilnosti previdno zadržani. Od avtorjev, ki izrazijo mnenje, jih večina, kot na primer Riemann[1] ali Bombieri[2] nakaže, da pričakujejo (ali vsaj upajo), da je pravilna. Med avtorji, ki izražajo resnični dvom o njej, sta Ivić,[122] ki navaja nekatere razloge za dvom, in Littlewood,[123] ki naravnost navaja svoje prepričanje, da je nepravilna in, da zanjo ne obstaja noben dokaz in predstavljiv vzrok za pravilnost. Med avtorji, ki so dvomili o pravilnosti Riemannove domneve, je bil tudi Turing.[114][4] V svojem članku je zapisal: »Naredili so se izračuni v optimističnem upanju, da bi se našla ničla zunaj kritične premice.« Turing je našel, da vse ničle do ležijo na kritični premici. Pregledni članki so si enotni, da je pokazateljev zanjo precej, vendar ne ogromno, tako da, medtem ko je verjetno pravilna, obstaja več upravičenih dvomov.[2][124][125]
Nekatere argumente za (ali proti) Riemannovi domnevi so navedli Sarnak,[125] Conrey[124] in Ivić.[122] Med njimi so naslednji razlogi:
- dokazali so že več analogonov Riemannove domneve. Deligneov dokaz za varietete čez končne obsege[59] je verjetno najmočnejši posamezen teoretični razlog v prid Riemannovi domnevi. To zagotavlja nekaj pokazateljev za splošnejšo domnevo, da za vse funkcije ζ, povezane z avtomorfnimi formami, velja Riemannova domneva, ki vsebuje klasično Riemannovo domnevo kot posebni primer. Podobno za Selbergove funkcije ζ velja analogon Riemannove domneve in so na nek način podobne Riemannovi funkciji ζ s funkcijsko enačbo in razvoj v neskončni produkt podoben razvoju v Eulerjev produkt. Obstaja pa nekaj večjih razlik: niso na primer podane s kakšno Dirichletovo vrsto. Riemannovo domnevo za Gossovo funkcijo ζ je dokazal Sheats.[66] Z razliko od teh pozitivnih primerov za nekatere Epsteinove funkcije ζ Riemannova domneva ne velja, četudi imajo neskončno število ničel na kritični premici.[19] Te funkcije so zelo podobne Riemannovi funkciji ζ, lahko se jih razvije s kakšno Dirichletovo vrsto in imajo funkcijsko enačbo, vendar tiste, za katere ne velja Riemannova domneva, nimajo Eulerjevega produkta in niso neposredno povezane z avtomorfnimi reprezentacijami.
- kot prvo se numerično preverjanje, da mnogo ničel leži na premici, zdi močan pokazatelj. Vendar je bilo v analitični teoriji števil veliko domnev, ki so jih podpirale velike količine numeričnih izračunov, pa so bile nepravilne. Glej Skewesovo število za značilni zgled, kje se prva izjema verjetni domnevi povezani z Riemannovo domnevo morda lahko pojavi pri približno številu 10316; protiprimer Riemannovi domnevi z imaginarnim delom takšne velikosti bi bil precej daleč proč od tega, kar se trenutno lahko izračuna z neposrednim pristopom. Problem je, ker na obnašanje velikokrat vplivajo zelo počasi naraščajoče funkcije, kot je npr. log log T, in težijo k neskončnosti, vendar zelo počasi, kar je nemogoče zaznati z računanjem. Takšne funkcije se pojavljajo v teoriji funkcij ζ in od njih je odvisno obnašanje njihovih ničel. Zgornja funkcija S(T) ima na primer povprečno velikost (log log T)1/2. Kot vrednost funkcije S(T) naraste vsaj za 2 v kakšnem protiprimeru Riemannove domneve, bi bilo pričakovati, da se bodo protiprimeri Riemannove domneve začeli pojavljati le kadar vrednost funkcije S(T) postane velika. Njena vrednost ni skoraj nikoli dosti večja od 3, kakor kažejo dosedanji izračuni, vendar je znano, da je neomejena, kar nakazuje, da izračuni še niso dosegli območja značilnega obnašanja funkcije ζ.
- Denjoyev verjetnostni argument za Riemannovo domnevo[15] temelji na opažanju, da, če je μ(x) naključno zaporedje števil »1« in »−1«, potem so za vsak ε > 0 delne vsote:
- (vrednosti, ki so lege v enostavnem naključnem sprehodu) omejene z:
- z verjetnostjo enako 1. Riemannova domneva je enakovredna tej meji za Möbiusovo funkcijo μ in Mertensovo funkcijo M, ki sta izpeljani iz nje na enak način. IZ drugimi besedami je v nekem smislu Riemannova domneva enakovredna izjavi, da se μ(x) obnaša kot naključno zaporedje metanja kovancev. Kadar je μ(x) neničelna, njen predznak da parnost števila prafaktorjev x, in tako Riemannova domneva neformalno pravi, da se parnost števila prafaktorjev celega števila obnaša naključno. Takšni verjetnostni argumenti v teoriji števil velikokrat dajo pravilen odgovor, vendar jih je težko strogo definirati, včasih pa dajo tudi nepravilen odgovor za kakšne rezultate, kot na primer za Maierjev izrek.
- Odlyzkovi izračuni[64] kažejo, da se ničle funkcije ζ obnašajo zelo podobno kot lastne vrednosti slučajne hermitske matrike, kar nakazuje, da so lastne vrednosti kakšnega sebiadjungiranega operatorja, od koder bi lahko izhajala pravilnost Riemannove domneve. Vsi poskusi najti takšen operator pa so do sedaj spodleteli.
- obstaja več izrekov, kot je na primer Goldbachova šibka domneva za dovolj velika liha števila, ki so bili najprej dokazani s privzetkom o pravilnosti posplošene Riemannove domneve, kasneje pa so se pokazali, da so pravilni brezpogojno. To se lahko obravnava kot šibek pokazatelj za pravilnost posplošene Riemannove domneve, saj se je več njenih »predvidenj« izkazalo za pravilne.
- Lehmerjev par,[115] kjer sta dve ničli včasih zelo blizu skupaj, je včasih dan kot razlog za nepravilnost Riemannove domneve. Vendar se to pričakuje, da se to slučajno pojavi le občasno četudi bi bila Riemannova domneva pravilna. Odlyzkovi izračuni nakazujejo, da se bližnji pari ničel pojavljajo ravno tako pogosto kot napoveduje Montgomeryjeva domneva o parni korelaciji. Ni znano ali obstaja neskončno mnogo Lehmerjevih parov.
- Patterson[16] predlaga, da je najbolj brezpogojen razlog za Riemannovo domnevo za večino matematikov upanje, da so praštevila porazdeljena enakomerno kot je mogoče.
Glej tudi[uredi | uredi kodo]
- razširjena Riemannova domneva
- posplošena Riemannova domneva
- velika Riemannova domneva
- Hilbertov osmi problem
- problemi tisočletne nagrade
- lokalna funkcija zeta
Opombe[uredi | uredi kodo]
- ↑ Če je s pozitivno celo število, ta argument ne velja, ker se ničle funkcije sinus poničijo s poli funkcije Γ, ker zavzame negativne celoštevilske argumente.
- ↑ Littlewood, 1912; glej na primer razdelek 14.25 v Titchmarshevem delu.[19]
- ↑ Za pomen teh simbolov glej Landauov simbol.
- ↑ V delu Heckeja in Heilbronna so edine L-funkcije, ki se pojavljajo, tiste povezane z imaginarnim kvadratnim karakterjem, in le tistim L-funkcijam, za katere je posplošena Riemannova domneva pravilna ali nepravilna, je namenjena; nepravilnost splošne Riemannove domneve za L-funkcije kubičnega Dirichletovega karakterja bi strogo govoreč pomenilo, da je splošna Riemannova domneva nepravilna, vendar takšne vrste nepravilnosti splošne Riemannove domneve Heilbronn ni imel v mislih, tako da je bil njegov privzetek bolj omejen kot le to, da je splošna Riemannova domneva napravilna.
- ↑ Mnogokratne ničle bi povzročile težave za algoritme iskanja ničel, ki so odvisni od iskanja sprememb predznaka med ničlami.
Sklici[uredi | uredi kodo]
- ↑ 1,0 1,1 1,2 Riemann (1859).
- ↑ 2,0 2,1 2,2 Bombieri (2000).
- ↑ Broughan; Barnett (2002).
- ↑ 4,0 4,1 4,2 Wolf (2009).
- ↑ Christ (2013).
- ↑ »Riemann hypothesis«. Ameriški matematični inštitut (v angleščini). 17. junij 2004. Pridobljeno 19. junija 2015.
- ↑ Wolf (2014), str. 7.
- ↑ Lagarias; Mehta (2015), str. 10.
- ↑ Calude; Hertling; Khoussainov (1997).
- ↑ Derbyshire (2003).
- ↑ Rockmore (2005).
- ↑ Sabbagh (2003a).
- ↑ Sabbagh (2003b).
- ↑ du Sautoy (2003).
- ↑ 15,0 15,1 Edwards (1974).
- ↑ 16,0 16,1 Patterson (1988).
- ↑ Borwein idr. (2008).
- ↑ Mazur; Stein (2015).
- ↑ 19,0 19,1 19,2 19,3 19,4 Titchmarsh (1986).
- ↑ 20,0 20,1 Ivić (1985).
- ↑ Karacuba; Voronin (1992).
- ↑ Riesel; Göhl (1970).
- ↑ Zagier (1977).
- ↑ Ingham (1932).
- ↑ von Koch (1901).
- ↑ Odlyzko; te Riele (1985).
- ↑ 27,0 27,1 Robin (1984).
- ↑ Franel; Landau (1924).
- ↑ Massias; Nicolas; Robin (1988).
- ↑ Lindelöf (1908).
- ↑ Nicely (1999).
- ↑ Riesz (1916).
- ↑ Nyman (1950).
- ↑ Beurling (1955).
- ↑ Li (1997).
- ↑ Coffey (2007).
- ↑ Arias de Reyna (2011).
- ↑ Matijasevič (2014).
- ↑ Speiser (1934).
- ↑ Salem (1953).
- ↑ Volčkov (1995).
- ↑ He; Jejjala; Minic (2015).
- ↑ Ramanudžan (1997).
- ↑ Akbary; Friggstad (2009).
- ↑ Choie idr. (2007).
- ↑ Lagarias (2002).
- ↑ Cisło; Wolf (2008).
- ↑ Conrad (2010).
- ↑ Weinberger (1973).
- ↑ Odlyzko (1990).
- ↑ Ono; Soundararajan (1997).
- ↑ Ireland; Rosen (1990), str. 359.
- ↑ Ingham (1932), §V.
- ↑ Ireland; Rosen (1990), str. 358–361.
- ↑ Ribenboim (1996), str. 320
- ↑ Artin (1924).
- ↑ Weil (1948).
- ↑ Weil (1949).
- ↑ 59,0 59,1 59,2 Deligne (1974).
- ↑ 60,0 60,1 Deligne (1980).
- ↑ Serre (1969–1970).
- ↑ Selberg (1956).
- ↑ Montgomery (1973).
- ↑ 64,0 64,1 64,2 64,3 Odlyzko (1987).
- ↑ Radziejewski (2007).
- ↑ 66,0 66,1 Sheats (1998).
- ↑ Wiles (2000).
- ↑ Watkins (2007).
- ↑ 69,0 69,1 Connes (1999).
- ↑ Deninger (1998).
- ↑ Leichtnam (2005).
- ↑ Zagier (1981).
- ↑ Cartier (1982).
- ↑ Schumayer; Hutchinson (2011).
- ↑ Knauf (1999).
- ↑ Turán (1948).
- ↑ Haselgrove (1958).
- ↑ Borwein; Ferguson; Mossinghoff (2008).
- ↑ Spira (1968).
- ↑ Montgomery (1983).
- ↑ Connes (2000).
- ↑ Lapidus (2008).
- ↑ de Branges (1992).
- ↑ Conrey; Li (2000).
- ↑ Dyson (2009).
- ↑ Fesenko (2010).
- ↑ Suzuki (2011).
- ↑ Kurokava (1992).
- ↑ 89,0 89,1 Selberg (1946).
- ↑ Ghosh (1983).
- ↑ Odlyzko (2002).
- ↑ Hadamard (1896).
- ↑ La Vallée Poussin (1896).
- ↑ La Vallée Poussin (1899–1900).
- ↑ Ford (2002).
- ↑ Hardy (1914).
- ↑ Hardy; Littlewood (1921).
- ↑ 98,0 98,1 Selberg (1942).
- ↑ Levinson (1974).
- ↑ Conrey (1989).
- ↑ Bohr; Landau (1914).
- ↑ Karacuba (1984a).
- ↑ Karacuba (1984b).
- ↑ Karacuba (1985).
- ↑ Karacuba (1992).
- ↑ Haselgrove; Miller (1960)
- ↑ Odlyzko.
- ↑ Siegel (1932).
- ↑ Gram (1903).
- ↑ Backlund (1914).
- ↑ Hutchinson (1925).
- ↑ Titchmarsh (1935).
- ↑ Titchmarsh (1936).
- ↑ 114,0 114,1 Turing (1953).
- ↑ 115,0 115,1 Lehmer (1956).
- ↑ 116,0 116,1 Rosser; Yohe; Schoenfeld (1969).
- ↑ van de Lune; te Riele; Winter (1986).
- ↑ Odlyzko (1992).
- ↑ Odlyzko (1998).
- ↑ Gourdon (2004).
- ↑ Trudgian (2011).
- ↑ 122,0 122,1 Ivić (2008).
- ↑ Littlewood (1962).
- ↑ 124,0 124,1 Conrey (2003).
- ↑ 125,0 125,1 Sarnak (2008).
Viri[uredi | uredi kodo]
- Akbary, Amir; Friggstad, Zachary (2009), »Superabundant numbers and the Riemann hypothesis« (PDF), Amer. Math. Monthly, 116 (3): 273–275, doi:10.4169/193009709X470128, arhivirano iz prvotnega spletišča (PDF) dne 11. aprila 2014, pridobljeno 26. junija 2015
- Arias de Reyna, Juan (26. september 2003). »X-Ray of Riemann zeta-function«. arXiv:math/0309433.
{{navedi arxiv}}: Prezrt|class=(pomoč) - Arias de Reyna, Juan (31. januar 2011), Asymptotics of Keiper-Li Coefficients (PDF)
- Artin, Emil (1924), »Quadratische Körper im Gebiete der höheren Kongruenzen. II. Analytischer Teil«, Mathematische Zeitschrift, 19 (1): 207–246, doi:10.1007/BF01181075
- Backlund, R. J. (1914), »Sur les Zéros de la Fonction ζ(s) de Riemann«, C. R. Acad. Sci. Paris, 158: 1979–1981
- Beurling, Arne (1955), »A closure problem related to the Riemann zeta-function«, Proceedings of the National Academy of Sciences of the United States of America, 41 (5): 312–314, doi:10.1073/pnas.41.5.312, MR 0070655
- Bohr, Harald; Landau, Edmund (1914), »Ein Satz über Dirichletsche Reihen mit Anwendung auf die ζ-Funktion und die L-Funktionen«, Rendiconti del Circolo Matematico di Palermo, 37 (1): 269–272, doi:10.1007/BF03014823
- Bombieri, Enrico (2000), The Riemann Hypothesis – official problem description (PDF), Clayjev matematični inštitut, arhivirano iz prvotnega spletišča (PDF) dne 22. decembra 2015, pridobljeno 25. oktobra 2008 Ponatisnjeno v (Borwein et al. 2008).
- Borwein, Peter; Choi, Stephen; Rooney, Brendan; Weirathmueller, Andrea; in sod., ur. (2008), The Riemann Hypothesis: A Resource for the Afficionado and Virtuoso Alike, CMS Books in Mathematics, New York: Springer, doi:10.1007/978-0-387-72126-2, ISBN 978-0-387-72125-5
- Borwein, Peter; Ferguson, Ron; Mossinghoff, Michael J. (2008), »Sign changes in sums of the Liouville function«, Mathematics of Computation, 77 (263): 1681–1694, doi:10.1090/S0025-5718-08-02036-X, MR 2398787
- de Branges, Louis (1992), »The convergence of Euler products«, Journal of Functional Analysis, 107 (1): 122–210, doi:10.1016/0022-1236(92)90103-P, MR 1165869
- Broughan, Kevin A.; Barnett, A. Ross (april 2002), The holomorphic flow of the Riemann Zeta function (PDF)
{{citation}}: Vzdrževanje CS1: samodejni prevod datuma (povezava) - Calude, Cristian S.; Hertling, Peter H.; Khoussainov, Bakhadyr (april 1997), Do the Zeros of Riemann's Zeta-Function Form a Random Sequence ? (PDF)
{{citation}}: Vzdrževanje CS1: samodejni prevod datuma (povezava) - Cartier, Pierre Emile Jean (1982), »Comment l'hypothèse de Riemann ne fut pas prouvée«, Seminar on Number Theory, Paris 1980–81 (Paris, 1980/1981), Progr. Math., zv. 22, Boston, MA: Birkhäuser Boston, str. 35–48, MR 0693308
- Choie, YoungJu; Lichiardopol, Nicolas; Moree, Pieter; Solé, Patrick (2007), »On Robin's criterion for the Riemann hypothesis«, Journal de théorie des nombres de Bordeaux, 19 (2): 357–372, arXiv:math.NT/0604314, doi:10.5802/jtnb.591, ISSN 1246-7405, MR 2394891, Zbl 1163.11059
- Christ, Thomas (2013). »Value-distribution of the Riemann zeta-function and related functions near the critical line«. arXiv:1405.1553 [math.NT]. Doktorska disertacija, Univerza v Würzburgu.
- Cisło, Jerzy; Wolf, Marek (13. avgust 2008). »Criteria equivalent to the Riemann Hypothesis«. arXiv:0808.0640 [math.NT].
- Coffey, Mark W. (Junij 2007), »The theta-Laguerre calculus formulation of the Li/Keiper constants«, Journal of Approximation Theory, 146 (2): 267–275, doi:10.1016/j.jat.2006.10.006
- Connes, Alain (1999), »Trace formula in noncommutative geometry and the zeros of the Riemann zeta function«, Selecta Mathematica. New Series, 5 (1): 29–106, arXiv:math/9811068, doi:10.1007/s000290050042, MR 1694895
- Connes, Alain (2000), »Noncommutative geometry and the Riemann zeta function«, Mathematics: frontiers and perspectives, Providence, R.I.: Ameriško matematično društvo, str. 35–54, MR 1754766
- Conrey, John Brian (1989), »More than two fifths of the zeros of the Riemann zeta function are on the critical line«, J. Reine angew. Math., 399: 1–16, doi:10.1515/crll.1989.399.1, MR 1004130
- Conrey, John Brian (2003), »The Riemann Hypothesis« (PDF), Notices of the American Mathematical Society: 341–353 Ponatisnjeno v (Borwein et al. 2008).
- Conrey, John Brian; Li, Xian-Jin (2000), »A note on some positivity conditions related to zeta and L-functions«, International Mathematics Research Notices, 2000 (18): 929–940, arXiv:math/9812166, doi:10.1155/S1073792800000489, MR 1792282
- Deligne, Pierre (1974), »La conjecture de Weil. I«, Publications Mathématiques de l'IHÉS, 43: 273–307, doi:10.1007/BF02684373, MR 0340258
- Deligne, Pierre (1980), »La conjecture de Weil : II«, Publications Mathématiques de l'IHÉS, 52: 137–252, doi:10.1007/BF02684780
- Deninger, Christopher (1998), »Some analogies between number theory and dynamical systems on foliated spaces«, Proceedings of the International Congress of Mathematicians, Vol. I (Berlin, 1998), Documenta Mathematica, str. 163–186, MR 1648030
- Derbyshire, John (2003), Prime Obsession, Joseph Henry Press, Washington, DC, ISBN 978-0-309-08549-6, MR 1968857
- Dyson, Freeman John (2009), »Birds and frogs« (PDF), Notices of the American Mathematical Society, 56 (2): 212–223, MR 2483565
- Edwards, Harold Mortimer (1974), Riemann's Zeta Function, New York: Dover Publications, ISBN 978-0-486-41740-0, MR 0466039
- Fesenko, Ivan Borisovič (2010), »Analysis on arithmetic schemes. II«, Journal of K-theory, 5 (3): 437–557, doi:10.1017/is010004028jkt103
- Ford, Kevin (2002), »Vinogradov's integral and bounds for the Riemann zeta function«, Proceedings of the London Mathematical Society. Third Series, 85 (3): 565–633, doi:10.1112/S0024611502013655, MR 1936814
- Franel, Jérôme; Landau, Edmund (1924), »Les suites de Farey et le problème des nombres premiers" (Franel, 198–201); "Bemerkungen zu der vorstehenden Abhandlung von Herrn Franel (Landau, 202–206)«, Göttinger Nachrichten: 198–206
- Ghosh, Amit (1983), »On the Riemann zeta function—mean value theorems and the distribution of |S(T)|«, J. Number Theory, 17: 93–102, doi:10.1016/0022-314X(83)90010-0
- Gourdon, Xavier (2004), The 1013 first zeros of the Riemann Zeta function, and zeros computation at very large height (PDF)
- Gram, Jørgen Pedersen (1903), »Note sur les zéros de la fonction ζ(s) de Riemann«, Acta Mathematica, 27: 289–304, doi:10.1007/BF02421310
- Granville, Andrew; Martin, Greg (2006), »Prime Number Races«, Amer. Math. Monthly, 113: 1–33, arXiv:math/0408319
- Hadamard, Jacques Salomon (1896), »Sur la distribution des zéros de la fonction ζ(s) et ses conséquences arithmétiques«, Bulletin Société Mathématique de France, 14: 199–220 Ponatisnjeno v (Borwein et al. 2008).
- Hardy, Godfrey Harold (1914), »Sur les Zéros de la Fonction ζ(s) de Riemann«, C. R. Acad. Sci. Paris, 158: 1012–1014, JFM 45.0716.04 Ponatisnjeno v (Borwein et al. 2008).
- Hardy, Godfrey Harold; Littlewood, John Edensor (1921), »The zeros of Riemann's zeta-function on the critical line«, Math. Z., 10 (3–4): 283–317, doi:10.1007/BF01211614
- Haselgrove, Colin Brian (1958), »A disproof of a conjecture of Pólya«, Mathematika, 5 (2): 141–145, doi:10.1112/S0025579300001480, ISSN 0025-5793, MR 0104638, Zbl 0085.27102 Ponatisnjeno v (Borwein et al. 2008).
- Haselgrove, Colin Brian; Miller, Jeffrey Charles Percy (1960), Tables of the Riemann zeta function, Royal Society Mathematical Tables, Vol. 6, Cambridge University Press, ISBN 978-0-521-06152-0, MR 0117905 Pregled
- He, Yang-Hui; Jejjala, Vishnu; Minic, Djordje (8. januar 2015). »From Veneziano to Riemann: A String Theory Statement of the Riemann Hypothesis«. arXiv:1501.01975 [hep-th].
- Hutchinson, John Irwin (1925), »On the Roots of the Riemann Zeta-Function«, Transactions of the American Mathematical Society, 27 (1): 49–60, doi:10.2307/1989163, JSTOR 1989163
- Ingham, Albert Edward (1932), The Distribution of Prime Numbers, Cambridge Tracts in Mathematics and Mathematical Physics, zv. 30, Cambridge University Press. Ponatisnjeno 1990, ISBN 978-0-521-39789-6,
- Ireland, Kenneth; Rosen, Michael Ira (1990), A Classical Introduction to Modern Number Theory (Second edition), New York: Springer, ISBN 0-387-97329-X
- Ivić, Aleksandar (1985), The Riemann Zeta Function, New York: John Wiley & Sons, ISBN 978-0-471-80634-9, MR 0792089 (Ponatisnjeno Dover 2003)
- Ivić, Aleksandar (2008), »On some reasons for doubting the Riemann hypothesis«, v Borwein, Peter; Choi, Stephen; Rooney, Brendan; Weirathmueller, Andrea; in sod. (ur.), The Riemann Hypothesis: A Resource for the Afficionado and Virtuoso Alike, CMS Books in Mathematics, New York: Springer, str. 131–160, arXiv:math.NT/0311162, ISBN 978-0-387-72125-5
- Karacuba, Anatolij Aleksejevič (1984a), »Zeros of the function ζ(s) on short intervals of the critical line«, Izv. Akad. Nauk SSSR, Ser. Mat. (v ruščini), 48 (3): 569–584, MR 0747251
- Karacuba, Anatolij Aleksejevič (1984b), »Distribution of zeros of the function ζ(1/2 + it)«, Izv. Akad. Nauk SSSR, Ser. Mat. (v ruščini), 48 (6): 1214–1224, MR 0772113
- Karacuba, Anatolij Aleksejevič (1985), »Zeros of the Riemann zeta-function on the critical line«, Trudy Mat. Inst. Steklov. (v ruščini) (167): 167–178, MR 0804073
- Karacuba, Anatolij Aleksejevič (1992), »On the number of zeros of the Riemann zeta-function lying in almost all short intervals of the critical line«, Izv. Ross. Akad. Nauk, Ser. Mat. (v ruščini), 56 (2): 372–397, MR 1180378
- Karacuba, Anatolij Aleksejevič; Voronin, Sergej Mihajlovič (1992), The Riemann zeta-function, de Gruyter Expositions in Mathematics, zv. 5, Berlin: Walter de Gruyter & Co., COBISS 2634073, ISBN 978-3-11-013170-3, MR 1183467
- Keating, Jonathan P.; Snaith, Nina C. (2000), »Random matrix theory and ζ(1/2 + it)«, Communications in Mathematical Physics, 214 (1): 57–89, doi:10.1007/s002200000261, MR 1794265
- Knauf, Andreas (1999), »Number theory, dynamical systems and statistical mechanics«, Reviews in Mathematical Physics. A Journal for Both Review and Original Research Papers in the Field of Mathematical Physics, 11 (8): 1027–1060, doi:10.1142/S0129055X99000325, MR 1714352
- von Koch, Helge (1901), »Sur la distribution des nombres premiers«, Acta Mathematica, 24: 159–182, doi:10.1007/BF02403071
- Kurokava, Nobušige (1992), »Multiple zeta functions: an example«, Zeta functions in geometry (Tokyo, 1990), Adv. Stud. Pure Math., zv. 21, Tokio: Kinokuniya, str. 219–226, MR 1210791
- Lagarias, Jeffrey Clark (2002), »An elementary problem equivalent to the Riemann Hypothesis«, Amer. Math. Monthly, 109: 534–543
- Lagarias, Jeffrey Clark; Mehta, Harsh (1. marec 2015). »Products of Farey fractions«. arXiv:1503.00199 [math.NT].
- Lapidus, Michel L. (2008), In search of the Riemann zeros, Providence, R.I.: Ameriško matematično društvo, ISBN 978-0-8218-4222-5, MR 2375028
- Lavrik, A. F. (2001), »Zeta-function«, v Hazewinkel, Michiel (ur.), Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Lehmer, Derrick Henry (1956), »Extended computation of the Riemann zeta-function«, Mathematika. A Journal of Pure and Applied Mathematics, 3 (2): 102–108, doi:10.1112/S0025579300001753, MR 0086083
- Leichtnam, Eric (2005), »An invitation to Deninger's work on arithmetic zeta functions«, Geometry, spectral theory, groups, and dynamics, Contemp. Math., zv. 387, Providence, RI: Ameriško matematično društvo, str. 201–236, MR 2180209
- Levinson, Norman (1974), »More than one-third of the zeros of Riemann's zeta function are on σ = 1/2«, Adv. In Math., 13 (4): 383–436, doi:10.1016/0001-8708(74)90074-7, MR 0564081
- Li, Xian-Jin (1997), »The positivity of a sequence of numbers and the Riemann hypothesis«, J. Number Theory, 65 (2): 325–333, doi:10.1006/jnth.1997.2137, MR 98d.11101
{{citation}}: Preveri vrednost|mr=(pomoč) - Lindelöf, Ernst Leonard (1908), »Quelques remarques sur la croissance de la fonction ζ(s)«, Bull. Sci. Math., 32: 341–356
- Littlewood, John Edensor (1962), »The Riemann hypothesis«, The scientist speculates: an anthology of partly baked idea, New York: Basic books
- van de Lune, J.; te Riele, Herman J. J.; Winter, D. T. (1986), »On the zeros of the Riemann zeta function in the critical strip. IV«, Mathematics of Computation, 46 (174): 667–681, doi:10.2307/2008005, JSTOR 2008005, MR 0829637
- Massias, J.-P.; Nicolas, Jean-Louis; Robin, Guy (1988), »Évaluation asymptotique de l'ordre maximum d'un élément du groupe symétrique«, Polska Akademia Nauk. Instytut Matematyczny. Acta Arithmetica, 50 (3): 221–242, MR 0960551
- Matijasevič, Jurij Vladimirovič (26. oktober 2014), Yet another representation for the sum of reciprocals of the nontrivial zeros of the Riemann zeta-function, arXiv:1410.7036
- Mazur, Barry; Stein, William Arthur (2007), What is Riemann’s Hypothesis? (PDF), arhivirano iz prvotnega spletišča (PDF) dne 27. marca 2009, pridobljeno 26. junija 2015
- Mazur, Barry; Stein, William Arthur (2015), Prime Numbers and the Riemann Hypothesis, arhivirano iz prvotnega spletišča dne 27. junija 2015, pridobljeno 26. junija 2015
- Montgomery, Hugh Lowell (1973), »The pair correlation of zeros of the zeta function«, Analytic number theory, Proc. Sympos. Pure Math., zv. XXIV, Providence, R.I.: Ameriško matematično društvo, str. 181–193, MR 0337821 Ponatisnjeno v (Borwein et al. 2008).
- Montgomery, Hugh Lowell (1983), »Zeros of approximations to the zeta function«, v Erdős, Paul (ur.), Studies in pure mathematics. To the memory of Paul Turán, Basel, Boston, Berlin: Birkhäuser, str. 497–506, ISBN 978-3-7643-1288-6, MR 0820245
- Nicely, Thomas R. (1999), »New maximal prime gaps and first occurrences«, Mathematics of Computation, 68 (227): 1311–1315, doi:10.1090/S0025-5718-99-01065-0, MR 1627813
- Nyman, Bertil (1950), On the One-Dimensional Translation Group and Semi-Group in Certain Function Spaces, PhD Thesis, Univerza v Uppsali: Univerza v Uppsali, MR 0036444
- Odlyzko, Andrew Michael; te Riele, Herman J. J. (1985), »Disproof of the Mertens conjecture«, Journal für die reine und angewandte Mathematik, 357 (357): 138–160, doi:10.1515/crll.1985.357.138, MR 0783538
- Odlyzko, Andrew Michael (1987), »On the distribution of spacings between zeros of the zeta function«, Mathematics of Computation, 48 (177): 273–308, doi:10.2307/2007890, JSTOR 2007890, MR 0866115
- Odlyzko, Andrew Michael (1990), »Bounds for discriminants and related estimates for class numbers, regulators and zeros of zeta functions: a survey of recent results«, Séminaire de Théorie des Nombres de Bordeaux, Série 2, 2 (1): 119–141, doi:10.5802/jtnb.22, MR 1061762
- Odlyzko, Andrew Michael (1992), The 1020-th zero of the Riemann zeta function and 175 million of its neighbors (PDF) Ta neobjavljena knjiga opisuje implementacijo algoritma in podrobno obravnava rezultate.
- Odlyzko, Andrew Michael (1998), The 1021st zero of the Riemann zeta function (PDF)
- Odlyzko, Andrew Michael (2000), »An improved bound for the de Bruijn-Newman constant«, Numerical Algorithms, 25 (1): 293–303
- Ono, Ken; Soundararajan, Kannan (1997), »Ramanujan's ternary quadratic form« (PDF), Inventiones Mathematicae, 130 (3): 415–454, doi:10.1007/s002220050191, arhivirano iz prvotnega spletišča (PDF) dne 15. septembra 2015, pridobljeno 26. junija 2015
- Patterson, S. J. (1988), An introduction to the theory of the Riemann zeta-function, Cambridge Studies in Advanced Mathematics, zv. 14, Cambridge University Press, ISBN 978-0-521-33535-5, MR 0933558
- Radziejewski, Maciej (2007), »Independence of Hecke zeta functions of finite order over normal fields«, Transactions of the American Mathematical Society, 359 (5): 2383–2394, doi:10.1090/S0002-9947-06-04078-5, MR 2276625,
Obstaja neskončno mnogo neizomorfnih obsegov algebrskih števil katerih Dedekindove funkcije ζ imajo neskončno mnogo netrivialnih mnogokratnih ničel.
- Ramanudžan, Srinivasa Ajangar (1997), »Highly composite numbers, annotated by Jean-Louis Nicolas and Guy Robin«, The Ramanujan Journal, 1 (2): 119–153, doi:10.1023/A:1009764017495, ISSN 1382-4090, MR 1606180
- Ribenboim, Paulo (1996), The New Book of Prime Number Records, New York: Springer, ISBN 0-387-94457-5
- Riemann, Bernhard (1859), »Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse«, Monatsberichte der Berliner Akademie. V Gesammelte Werke, Teubner, Leipzig (1892), ponatisnjeno Dover, New York (1953). Izvirni rokopis Arhivirano 2013-05-23 na Wayback Machine. (z angleškim prevodom). Ponatisnjeno v (Borwein et al. 2008) in (Edwards 1974)
- Riesel, Hans; Göhl, Gunnar (1970), »Some calculations related to Riemann's prime number formula«, Mathematics of Computation, 24 (112): 969–983, doi:10.2307/2004630, JSTOR 2004630, MR 0277489
- Riesz, Marcel (1916), »Sur l'hypothèse de Riemann«, Acta Mathematica, 40: 185–190, doi:10.1007/BF02418544
- Robin, Guy (1984), »Grandes valeurs de la fonction somme des diviseurs et hypothèse de Riemann«, Journal de Mathématiques Pures et Appliquées, Neuvième Série, 63 (2): 187–213, MR 0774171
- Rockmore, Dan (2005), Stalking the Riemann hypothesis, Pantheon Books, ISBN 978-0-375-42136-5, MR 2269393
- Rosser, John Barkley; Yohe, J. M.; Schoenfeld, Lowell (1969), »Rigorous computation and the zeros of the Riemann zeta-function. (With discussion)«, Information Processing 68 (Proc. IFIP Congress, Edinburgh, 1968), Vol. 1: Mathematics, Software, Amsterdam: North-Holland, str. 70–76, MR 0258245
- Rudin, Walter (1973), Functional Analysis, 1st edition (January 1973), New York: McGraw-Hill, ISBN 0-070-54225-2
- Sabbagh, Karl (2003a), The Riemann hypothesis, New York: Farrar, Straus and Giroux, ISBN 978-0-374-25007-2, MR 1979664
- Sabbagh, Karl (2003b), Dr. Riemann's zeros, London: Atlantic Books, ISBN 978-1-843-54101-1
- Salem, Raphaël (1953), »Sur une proposition équivalente à l'hypothèse de Riemann«, Les Comptes rendus de l'Académie des sciences, 236: 1127–1128, MR 0053148
- Sarnak, Peter (2008), »Problems of the Millennium: The Riemann Hypothesis«, v Borwein, Peter; Choi, Stephen; Rooney, Brendan; Weirathmueller, Andrea; in sod. (ur.), The Riemann Hypothesis: A Resource for the Afficionado and Virtuoso Alike (PDF), CMS Books in Mathematics, New York: Springer, str. 107–115, ISBN 978-0-387-72125-5, arhivirano iz prvotnega spletišča (PDF) dne 13. aprila 2016, pridobljeno 26. junija 2015
- du Sautoy, Marcus (2003), The music of the primes, HarperCollins Publishers, ISBN 978-0-06-621070-4, MR 2060134
- Schoenfeld, Lowell (1976), »Sharper bounds for the Chebyshev functions θ(x) and ψ(x). II«, Mathematics of Computation, 30 (134): 337–360, doi:10.2307/2005976, JSTOR 2005976, MR 0457374
- Schumayer, Daniel; Hutchinson, David A. W. (2011). »Physics of the Riemann Hypothesis«. arXiv:1101.3116 [math-ph].
- Selberg, Atle (1942), »On the zeros of Riemann's zeta-function«, Skr. Norske Vid. Akad. Oslo I., 10: 59 pp, MR 0010712
- Selberg, Atle (1946), »Contributions to the theory of the Riemann zeta-function«, Arch. Math. Naturvid., 48 (5): 89–155, MR 0020594
- Selberg, Atle (1956), »Harmonic analysis and discontinuous groups in weakly symmetric Riemannian spaces with applications to Dirichlet series«, J. Indian Math. Soc. (N.S.), 20: 47–87, MR 0088511
- Serre, Jean-Pierre (1969–1970), »Facteurs locaux des fonctions zeta des varietés algébriques (définitions et conjectures)«, Séminaire Delange-Pisot-Poitou, 19
- Sheats, Jeffrey T. (1998), »The Riemann hypothesis for the Goss zeta function for Fq[T]«, J. Number Theory, 71 (1): 121–157, doi:10.1006/jnth.1998.2232, MR 1630979
- Siegel, Carl Ludwig (1932), »Über Riemanns Nachlaß zur analytischen Zahlentheorie«, Quellen Studien zur Geschichte der Math. Astron. und Phys. Abt. B: Studien 2: 45–80 Ponatisnjeno v Gesammelte Abhandlungen, Vol. 1. Berlin: Springer-Verlag, 1966.
- Speiser, Andreas (1934), »Geometrisches zur Riemannschen Zetafunktion«, Mathematische Annalen, 110: 514–521, doi:10.1007/BF01448042, JFM 60.0272.04, arhivirano iz prvotnega spletišča dne 27. junija 2015, pridobljeno 26. junija 2015
- Spira, Robert (1968), »Zeros of sections of the zeta function. II«, Mathematics of Computation, 22: 163–173, doi:10.2307/2004774, MR 0228456
- Suzuki, Masatoši (2011), »Positivity of certain functions associated with analysis on elliptic surfaces«, J. Number Theory, 131 (10): 1770–1796, doi:10.1016/j.jnt.2011.03.007
- Titchmarsh, Edward Charles (1935), »The Zeros of the Riemann Zeta-Function«, Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, Kraljeva družba, 151 (873): 234–255, doi:10.1098/rspa.1935.0146, JSTOR 96545
- Titchmarsh, Edward Charles (1936), »The Zeros of the Riemann Zeta-Function«, Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, Kraljeva družba, 157 (891): 261–263, doi:10.1098/rspa.1936.0192, JSTOR 96692
- Titchmarsh, Edward Charles (1986), The theory of the Riemann zeta-function (2. izd.), The Clarendon Press Oxford University Press, ISBN 978-0-19-853369-6, MR 0882550
- Trudgian, Timothy (2011), »On the success and failure of Gram's Law and the Rosser Rule«, Acta Arithmetica, 125 (3): 225–256, doi:10.4064/aa148-3-2
- Turán, Paul (1948), »On some approximative Dirichlet-polynomials in the theory of the zeta-function of Riemann«, Danske Vid. Selsk. Mat.-Fys. Medd., 24 (17): 36, MR 0027305 Ponatisnjeno v (Borwein et al. 2008).
- Turing, Alan Mathison (1953), »Some calculations of the Riemann zeta-function«, Proc. London Math. Soc.. Third Series, 3 (1): 99–117, doi:10.1112/plms/s3-3.1.99, MR 0055785
- La Vallée Poussin, Charles-Jean de (1896), »Recherches analytiques sur la théorie des nombers premiers«, Ann. Soc. Sci. Bruxelles, 20: 183–256
- La Vallée Poussin, Charles-Jean de (1899–1900), »Sur la fonction ζ(s) de Riemann et la nombre des nombres premiers inférieurs à une limite donnée«, Mem. Couronnes Acad. Sci. Belg., 59 (1) Ponatisnjeno v (Borwein et al. 2008).
- Volčkov, V. V. (Marec 1995), »On an equality equivalent to the Riemann hypothesis«, Ukrainian Mathematical Journal, 47 (3): 491–493, doi:10.1007/BF01056314
- Weil, André (1948), Sur les courbes algébriques et les variétés qui s'en déduisent, Actualités Sci. Ind., no. 1041 = Publ. Inst. Math. Univ. Strasbourg 7 (1945), Hermann et Cie., Paris, MR 0027151
- Weil, André (1949), »Numbers of solutions of equations in finite fields«, Bulletin of the American Mathematical Society, 55 (5): 497–508, doi:10.1090/S0002-9904-1949-09219-4, MR 0029393 Ponatisnjeno v in Oeuvres Scientifiques/Collected Papers by Andre Weil ISBN 0-387-90330-5
- Weinberger, Peter Jay (1973), »On Euclidean rings of algebraic integers«, Analytic number theory ( St. Louis Univ., 1972), Proc. Sympos. Pure Math., zv. 24, Providence, R.I.: Ameriško matematično društvo, str. 321–332, MR 0337902
- Wiles, Andrew (2000), »Twenty years of number theory«, Mathematics: frontiers and perspectives, Providence, R.I.: Ameriško matematično društvo, str. 329–342, ISBN 978-0-8218-2697-3, MR 1754786
- Wolf, Marek (8. oktober 2009). »Failed attempt to disproof the Riemann Hypothesis«. arXiv:0910.1534 [math.NT].
- Wolf, Marek (9. oktober 2014). »Will a physicists prove the Riemann Hypothesis?«. arXiv:1410.1214 [math-ph].
- Zagier, Don (1977), »The first 50 million prime numbers« (PDF), Math. Intelligencer, Springer, 0: 7–19, doi:10.1007/BF03039306, MR 0643810, arhivirano iz prvotnega spletišča (PDF) dne 27. marca 2009, pridobljeno 26. junija 2015
- Zagier, Don (1981), »Eisenstein series and the Riemann zeta function«, Automorphic forms, representation theory and arithmetic (Bombay, 1979), Tata Inst. Fund. Res. Studies in Math., zv. 10, Tata Inst. Fundamental Res., Bombay, str. 275–301, MR 0633666
Zunanje povezave[uredi | uredi kodo]
- Ameriški matematični inštitut, Riemann hypothesis (angleško)
- Apostol, Tom Mike, Where are the zeros of zeta of s? (v angleščini) Pesem o Riemannovi domnevi, avtor John Derbyshire.
- Borwein, Peter, The Riemann Hypothesis (PDF) (v angleščini), arhivirano iz prvotnega spletišča (PDF) dne 27. marca 2009, pridobljeno 26. junija 2015 (diapozitivi za predavanje)
- Conrad, K. (2010), Consequences of the Riemann hypothesis (v angleščini)
- Conrey, J. Brian; Farmer, David W., Equivalences to the Riemann hypothesis (v angleščini), arhivirano iz prvotnega spletišča dne 16. marca 2010, pridobljeno 26. junija 2015
- Gourdon, Xavier; Sebah, Pascal (2004), Computation of zeros of the Zeta function (v angleščini) (Pregledi domneve GUE, priložena je tudi obsežna bibliografija).
- Odlyzko, Andrew Michael, Home page (v angleščini) vključno s članki o ničlan funkcije zeta in razpredelnicami ničel funkcije zeta
- Odlyzko, Andrew Michael (2002), Zeros of the Riemann zeta function: Conjectures and computations (PDF) (v angleščini) Diapozitivi predavanja
- Pegg, Ed (2004), Ten Trillion Zeta Zeros (v angleščini), Math Games website, arhivirano iz prvotnega spletišča dne 2. novembra 2004, pridobljeno 26. junija 2015. razprava o izračunu Xavierja Gourdona prvih deset bilijonov netrivialnih ničel
- Pugh, Glen, The Riemann Hypothesis in a Nutshell, Java applet for plotting Z(t) (v angleščini), arhivirano iz prvotnega spletišča dne 30. junija 2015, pridobljeno 26. junija 2015
- Rubinstein, Michael, algorithm for generating the zeros (v angleščini), arhivirano iz prvotnega spletišča dne 27. aprila 2007, pridobljeno 26. junija 2015
- du Sautoy, Marcus (2006), Prime Numbers Get Hitched (v angleščini), Seed Magazine, arhivirano iz prvotnega spletišča dne 22. septembra 2017, pridobljeno 26. junija 2015
- Stein, William Arthur, What is Riemann's hypothesis (v angleščini), arhivirano iz prvotnega spletišča dne 4. januarja 2009, pridobljeno 26. junija 2015
- de Vries, Andreas (2004), The Graph of the Riemann Zeta function ζ(s) (v angleščini), preprosti animirani Java applet.
- Watkins, Matthew R. (18. julij 2007), Proposed proofs of the Riemann Hypothesis (v angleščini)[mrtva povezava]
- Zetagrid (2002) Distribuirani računalniški projekt, ki je poskušal ovreči Riemannovo domnevo; zaključen novembra 2005 (angleško)




























![{\displaystyle [a,b]\subseteq [0,1]\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60d9b5cd350edf24936136d2ff923d5c806c8fba)








































![{\displaystyle P_{n}(\gamma _{0},\ldots ,\gamma _{n-1})=\lambda _{n}=\sum _{\rho }\left[1-\left(1-{\frac {1}{\rho }}\right)^{n}\right]\!\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f9723eb332b97cf0eb6f9fdf375b1eff64ad7d9)































![{\displaystyle [x,p]=1/2\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/632487622cb283e36d1985a88377d05ed534dd9a)

































![{\displaystyle (T,T+H]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1a7e3fd02e456832dd42a5f2f366ef1f59b979c)





























