Banachov prostor
Banachov prôstor [banahov ~] je v matematiki in še posebej funkcionalni analizi polni normirani vektorski prostor. Tako je vektorski prostor z metriko, ki omogoča izračunavanje vektorske dolžine in razdalje med vektorji in je poln v smislu, da Cauchyjevo zaporedje vedno konvergira k dobro definirani limiti znotraj prostora.
Banachovi prostori se imenujejo po poljskem matematiku Stefanu Banachu, ki je uvedel ta koncept in ga sistematično proučeval med letoma 1920 in 1922 skupaj s Hansom Hahnom in Eduardom Hellyjem.[1] Maurice René Fréchet je prvi uporabil izraz »Banachov prostor«, nato pa je Banach skoval izraz »Fréchetov prostor«.[2]:93 Banachovi prostori so izvirno nastali iz zgodnejše raziskave o funkcijskih prostorih Davida Hilberta, Frécheta in Frigvesa Riesza. Banachovi prostori imajo osrednjo vlogo v funkcionalni analizi. Na drugih področjih matematične analize so prostori, ki se raziskujejo, velikokrat Banachovi.
Definicija[uredi | uredi kodo]
Banachov prostor je polni normirani vektorski prostor . Normirani prostor je par[a] , sestavljen iz vektorskega prostora nad skalarnim poljem (kjer je običajno ali ) skupaj z razločno[b] normo . Kot vse norme tudi ta norma inducira translacijsko invariantno[c] funkcijo razdalje, imenovano kanonična ali (normno) inducirana metrika, definirana za vse vektorje z:[d]
To naredi v metrični prostor . Zaporedje se imenuje Cauchyjevo v ali -Cauchyjevo ali -Cauchyjevo, če za vsako realno število obstaja nek tak indeks , da velja:
kadarkoli sta in večja od . Normirani prostor se imenuje Banachov prostor, kanonična metrika pa se imenuje polna metrika, če je polni metrični prostor, kar po definiciji pomeni, da za vsako Cauchyjevo zaporedje v obstaja nek takšen , da velja:
kjer se zaradi ta konvergenca zaporedja lahko enakovredno izrazi kot:
Norma normiranega prostora se imenuje polna norma, če je Banachov prostor.
L-polskalarni produkt
Za vsak normiran prostor obstaja takšen L-polskalarni produkt na , da velja za vse . V splošnem je lahko neskončno mnogo L-polskalarnih produktov, ki zadovoljujejo temu pogoju. L-polskalarni produkti so posplošitev prostorov skalarnih produktov, ki so tisto, po čemer se Hilbertovi prostori bistveno razlikujejo od vseh drugih Banachovih prostorov. To kaže, da se lahko vse normirane prostore (in s tem vse Banachove prostore) obravnava kot posplošitve (pre)hilbertovih prostorov.
Karakterizacija v smislu vrste
Struktura vektorskega prostora omogoča, da se poveže obnašanje Cauchyjevih zaporedij z obnašanjem konvergenčnih zaporedij vektorjev. Normirani prostor je Banachov, če in samo če vsaka absolutno konvergentna vrsta v konvergira v .[3]
Topologija[uredi | uredi kodo]
Kanonična metrika normiranega prostora inducira običajno metrično topologijo na , ki se imenuje kanonična ali normno inducirana topologija. Za vsak normirani prostor se samodejno privzema, da nosi to Hausdorffovo topologijo, razen če ni navedeno drugače. S to topologijo je vsak Banachov prostor Baireov prostor, leprav obstajajo normirani prostori, ki so Baireovi, na pa Banachovi.[4] Norma je vedno zvezna funkcija glede na topologijo, ki jo inducira.
Odprta in zaprta krogla polmera s središčem v točki sta torej množici:
Vsaka takšna krogla je konveksna in omejena podmnožica , vendar kompaktna krogla/okolica obstaja, če in samo če je končnorazsežni vektorski prostor. Še posebej noben neskončnorazsežni normirani prostor ne more biti krajevno kompakten ali imeti Heine-Borelove značilnosti. Če je vektor in skalar, potem velja:
Če se uporabi , se vidi, da je ta z normo inducirana topologija translacijsko invariantna, kar pomeni, da za kateri koli in je podmnožica odprta (in zaprta) v , če in samo če to velja za njeno translacijo . Posledično je topologija, inducirana z normo, v celoti določena s katero koli bazo okolice v izhodišču. Nekatere pogoste baze okolic na izhodišču vključujejo:
kjer je zaporedje pozitivnih realnih šštevil, ki konvergira k v (kot je na primer ali ). Tako se lahko na primer vsaka odprta podmnožica prostora zapiše kot unija:
indeksirana s kakšno podpmnožico , kjer se lahko vsak izbere iz zgoraj omenjenega zaporedja (odprte krogle se lahko zamenjajo z zaprtimi, čeprav se morajo zamenjati tudi indeksna množica in polmeri ). Poleg tega se lahko vedno izbere kot števna, če je separabilni prostor, kar po definiciji pomeni, da vsebuje kakšno števno gosto podmnožico.
Razredi homeomorfizmov separabilnih Banachovih prostorov
Vsi končnorazsežni normirani prostori so separabilni Banachovi prostori in poljubna dva Banachova prostora z enako končno razsežnostjo sta linearno homeomorfna. Vsak separabilni končnorazsežni Hilbertov prostor je linearno izometrično izomorfen separabilnemu Hilbertovemu prostoru zaporedja s svojo običajno normo .
Anderson-Kadecov izrek pravi, da je vsak neskončnorazsežni separabilni Fréchetov prostor homeomorfen produktnemu prostoru števno mnogih kopij (ta homeomorfizem ni treba da je linearna transformacija).[5][6] Tako so vsi neskončnorazsežni separabilni Fréchetovi prostori homeomorfni med seboj (ali rečeno drugače – njihova topologija je edinstvena do homeomorfizma). Ker je vsak Banachov prostor Fréchetov, velja to tudi za vse neskončnorazsežne separabilne Banachove prostore, vključno z . je dejansko homeomorfen celo svoji lastni enotski sferi , kar je v ostrem nasprotju s končnorazsežnimi prostori (evklidska ravnina na primer ni homeomorfna enotski krožnici).
Ta vzorec v razredih homeomorfizmov se razširi na posplošitve metrizabilnih (krajevno evklidskih) topoloških mnogoterosti, znanih kot metrične Banachove mnogoterosti in so metrični prostori, ki so okrog vsake točke, krajevno homeomorfni poljubni odprti podmnožici danega Banachovega prostora (metrične Hilbertove mnogoterosti in metrične Fréchetove mnogoterosti so definirane podobno).[6] Vsaka odprta podmnožica Banachovega prostora je na primer kanonično metrična Banachova mnogoterost po vzoru na , ker je inkluzivna preslikava odprti krajevni homeomorfizem. Z uporabo mikrosvežnjev Hilbertovega prostora je David Wilson Henderson leta 1969[7] pokazal, da je vsako metrično mnogoterost, modelirano na separabilnem neskončnorazsežnem Banachovem (ali Fréchetovem) prostoru, mogoče topološko vložiti kot odprto podmnožico , kar posledično tudi dopušča edinstveno gladko strukturo, zaradi česar je Hilbertova mnogoterost .
Kompaktne in konveksne podmnožice
Obstaja kompaktna podmnožica od katere konveksna ogrinjača ni zaprta in zato tudi ni kompaktna (za primer glej to opombo [e]).[8] Vendar, kot v vseh Banachovih prostorih, bo zaprta konveksna ogrinjača te (in vsake druge) kompaktne podmnožice kompaktna.[9]:145 Toda če normirani prostor ni poln, potem na splošno ni zagotovljeno da bo kompaktna kadar je kompaktna . Zgled[e] se lahko najde celo v (nepolnem) prehilbertovem vektorskem podprostoru .
Kot topološki vektorski prostor
Ta z normo inducirana topologija prav tako omogoča v tisto, kar je znano kot topološki vektorski prostor, ki je po definiciji vektorski prostor, opremljen s topologijo, ki naredi operacije seštevanja in skalarnega množenja zvezne. Poudarja se, da je topološki vektorski prostor je le vektorski prostor skupaj z določeno vrsto topologije; to pomeni, da ko se obravnava kot topološki vektorski prostor, ni povezan z nobeno posebno normo ali metriko (obe sta »pozabljeni«). Ta Hausdorffov topološki vektorski prostor je celo krajevno konveksen, ker množica vseh odprtih krogel s središčem v izhodišču tvori bazo okolice v izhodišču, ki jo sestavljajo konveksne uravnotežene odprte množice. Ta topološki vektorski prostor je tudi normirajoč, kar se po definiciji nanaša na vsak topološki vektorski prostor, katerega topologijo inducira neka (morda neznana) norma. Za normirajoče topološke vektorske prostore je značilno, da so Hausdorffovi in imajo omejeno konveksno okolico izhodišča. Vsi Banachovi prostori so sodasti prostori, kar pomeni, da je vsak sod okolica izhodišča (vse zaprte krogle s središčem v izhodišču so na primer sodi) in zagotavlja, da Banach-Steinhausov izrek velja.
Primerjava polnih metrizabilnih vektorskih topologij
Izrek o odprti preslikavi (Banach-Schauderjev izrek ali Banachov izrek) implicira, da če sta in topologiji na , ki naredita tako kot polna metrizabilna topološka vektorska prostora (na primer Banachove ali Fréchetove prostore) in, če je ena topologija bolj fina ali groba od druge, morata biti enaki, (to je, če ali , potem .)[9]:166–173 Tako na primer, če sta in Banachova prostora s topologijama in , in, če ima eden od teh prostorov kakšno odprto kroglo, ki je tudi odprta podmnožica drugega prostora (ali enakovredno, če je eden od ali zvezen), potem sta njuni topologiji enaki in njuni normi enakovredni.
Polnost[uredi | uredi kodo]
Polne norme in ekvivalentne norme
Dve normi in na vektorskem prostoru sta ekvivalentni, če inducirata isto topologijo.[10] To se zgodi, če in samo če obstajata takšni pozitivni realni števili , da velja za vse . Če sta in dve ekvivalentni normi na vektorskem prostoru , potem je Banachov prostor, če in samo če je tudi Banachov prostor. Glej to opombo za primer zvezne norme na Banachovem prostoru, ki ni ekvivalentna dani normi tega Banachovega prostora.[f][10] Vse norme na končnorazsežnem vektorskem prostoru so ekvivalentne in vsak končnorazsežni normirani prostor je Banachov prostor.[11]
Polne norme proti polnim metrikam
Metrika na vektorskem prostoru je inducirana z normo na , če ina samo če je translacijska invarianta[c] in absolutno homogena, kar pomeni, da velja za vse skalarje in vse – tem primeru funkcija definira normo na in kanonična metrika, ki jo inducira , je enaka .
Naj je normirani prostor in naj je normna topologija inducirana na . Predpostavi se, da je takšna poljubna metrika na , da je topologija , ki se inducira na enaka . Če je translacijska invarianta,[c] potem je Banachov prostor, če in samo če je polni metrični prostor.[2]:47-66 Če ni translacijska invarianta, je možno da je Banachov prostor, vendar ni polni metrični prostor[2]:47-51 (glej opombo[g] za primer). Nasprotno Kleejev izrek,[12][13][h] ki tudi velja za vse metrizabilne topološke vektorske prostore, nakazuje, da če obstaja poljubna[i] polna metrika na , ki inducira normno topologijo na , potem je Banachov prostor.
Fréchetov prostor je krajevno konveksni topološki vektorski prostor katerega topologija inducira neka translacijsko invariantna polna metrika. Vsak Banachov prostor je Fréchetov prostor, obratno pa ne velja – res, obstajajo tudi Fréchetovi prostori na katerih nobena norma ni zvezna funkcija, (kot je na primer prostor realnih zaporedij s produktno topologijo). Vendar pa je topologija vsakega Fréchetovega prostora inducirana z neko števno družino realnih (nujno zveznih) preslikav, imenovanih polnorme, ki so posplošitve norm. Možno je celo, da ima Fréchetov prostor topologijo, ki jo inducira števna družina norm, (takšne norme bi bile nujno zvezne),[j][9]:57–69 vendar prostor ne bi bil Banachov/normizabilen, ker njegovo topologijo ne more definirati katera koli posamezna norma. Zgled takšnega prostora je Fréchetov prostor , katerega definicijo se lahko najde v članku o prostorih testnih funkcij in porazdelitev.
Polne norme proti polnim topološkim vektorskim prostorom
Obstaja še en pojem polnosti poleg metrične polnosti in to je pojem polnega topološkega vektorskega prostora, ki uporablja teorijo uniformnih prostorov. Še posebej pojem polnega topološkega vektorskega prostora uporablja edinstveno translacijsko invariantno uniformnost, imenovano kanonična uniformnost, ki je odvisna le od vektorskega odštevanja in topologije , s katero je opremljen vektorski prostor, in zato je zlasti ta pojem polnega topološkega vektorskega prostora neodvisen od katere koli norme, ki je inducirala topologijo (in velja celo za topološke vektorske prostore, ki sploh niso metrizabilni). Vsak Banachov prostor je poln topološki vektorski prostor. Poleg tega je normirani prostor Banachov prostor (to pomeni, da je njegova z normo inducirana metrika polna), če in samo če je polna kot topološki vektorski prostor. Če je metrizabilni topološki vektorski prstor, (kot je na primer katera koli z normo inducirana topologija), potem je poln topološki vcektorski prostor, kar pomeni, da je dovolj preveriti, ali vsako Cauchyjevo zaporedje v konvergira v k neki točki , (to pomeni, da ni treba upoštevati bolj splošnega pojma poljubnih Cauchyjevih mrež).
Če je topološki vektorski prostor, katerega topologijo inducira poljubna (mogoče nezana) norma, (takšni prostori se imenujejo normizabilni), potem je polni topološki vektorski prostor, če in samo če se lahko priredi norma , ki na inducira topologijo in naredi Banachov prostor. Hausdorffov krajevno konveksni topološki vektorski prostor je normizabilen, če in samo če je močno dualni prostor normizabilen[9]:201 – v tem primeru je Banachov prostor, ( označuje močno dualni prostor , katerega topologija je posplošitev topologije, inducirane z dualno normo na zveznem dualnem prostoru – glej to opombo[k] za več podrobnosti). Če je metrizabilni krajevno konveksni topološki vektorski prostor, potem je normizabilen, če in samo če je Fréchet-Urysohnov prostor.[14] To kaže, da so v kategoriji krajevno konveksnih topoloških vektorskih prostorov Banachovi prostori točno tisti polni prostori, ki so hkrati metrizabilni in imajo metrizabilne močne dualne prostore.
Zapolnitve[uredi | uredi kodo]
Vsak normirani prostor je mogoče izometrično vložiti v gosti vektorski podprostor nekega Banachovega prostora, kjer se ta Banachov prostor imenuje zapolnitev normiranega prostora. Ta Hausdorffova zapolnitev je edinstvena do izometričnega izomorfizma.
Natančneje, za vsak normirani prostor obstaja Banachov prostor in takšno preslikavo , tako da je izometrična preslikava in gosta v . Če je še en takšen Banachov prostor, da obstaja izometrični izomorfizem iz na gosto podmnožico , potem je izometrično izomorfen . Ta Banachov prostor je Hausdorffova zapolnitev normiranega prostora . Osnovni metrični prostor za je enak kot metrična zapolnitev z operacijami vektorskega prostora, razširjenimi iz do . Zapolnitev se včasih označuje kot .
Splošna teorija[uredi | uredi kodo]
Linearni operatorji, izomorfizmi[uredi | uredi kodo]
Če sta in normirana prostora nad istim talnim poljem , se množica vseh zveznih -linearnih preslikav označuje kot . V neskončnorazsežnih prostorih vse linearne preslikave niso zvezne. Linearna preslikava iz normiranega prostora na drugi normirani prostor je zvezna, če in samo če je omejena na zaprto enotsko kroglo prostora . Tako se lahko vektorskemu prostoru da norma operatorja:
Za Banachov prostor je prostor Banachov prostor glede na to normo. V kategoričnih kontekstih je včasih priročno omejiti funkcijski prostor med dvema Banachovim prostoroma samo na kratke preslikave – v tem primeru se prostor ponovno pojavi kot naravni bifunktor.[15]
Če je Banachov prostor, prostor tvori unitalno Banachovo algebro – operacija množenja je dana s kompozicijo linearnih preslikav.
Če sta in normirana prostora, potem sta izomorfno normirana prostora, če obstaja takšna linearna bijekcija , da sta in njen inverz zvezni. Če je eden od prostorov ali poln (ali refleksiven, separabilen, itd.), potem je tak tudi drugi prostor. Dva normirana prostora in sta izometrično izomorfna, če je naprej tudi izometrija, kar pomeni, da je za vse v . Banach-Mazurjeva razdalja med dvema izomorfnima, vendar ne izometričnima, prostoroma in podaja mero za koliko se dva prostora in razlikujeta med seboj.
Zvezne in omejene linearne funkcije in polnorme[uredi | uredi kodo]
Vsak zvezni linearni operator je omejeni linearni operator in če se obravnavajo le normiranimi prostori, velja tudi obratno. To pomeni, da je linearni operator med dvema normiranima prostoroma omejen, če in samo če je zvezna funkcija. Še posebej zato, ker je skalarno polje (ki je ali ) normirani prostor, linearni funkcional na normiranem prostoru je omejeni linearni funkcional, če in samo če je zvezni linearni funkcional. To omogoča, da se rezultati, povezani z zveznostjo (kot so tisti spodaj), uporabijo za Banachove prostore. Čeprav je omejenost enaka kot zveznost za linearne preslikave med normiranimi prostori, se izraz »omejen« pogosteje uporablja, ko se obravnava predvsem Banachove prostore.
Če je podaditivna funkcija, (kot je norma, podlinearna funkcija ali realni linearni operator), potem[2]:192-193 je zvezna v izhodišču, če in samo če je uniformno zvezna na celotnem prostoru in, če poleg tega velja , je zvezna, če in samo če je njena absolutna vrednost zvezna. To se zgodi, če in samo če je odprta podmnožica .[2]:192-193[l] In kar je zelo pomembno za uporabo Hahn-Banachovega izreka – linearni funkcional je zvezen, če in samo če to velja za njegov realni del in še več, za in realni del popolnoma določa , zato je Hahn-Banachov izrek pogosto naveden samo za realne linearne funkcionale. Tudi linearni funkcional na je zvezen, če in samo če je polnorma zvezna, kar se zgodi, če in samo če obstaja takšna zvezna polnorma , da je . Ta zadnja izjava vključuje linearni funkcional in polnorma se najde v mnogih različicah Hahn-Banachovega izreka.
Osnovni pojmi[uredi | uredi kodo]
Kartezični produkt dveh normiranih prostorov kanonično ni opremljen z normo. Običajno pa se rabi več enakovrednih norm,[16]:182 kot na primer:
kar zaporedoma odgovarja koproduktu in produktu v kategoriji Banachovih prostorov in kratkih preslikav (obravnavano zgoraj).[15] Za končne (ko)produkte te norme povzročijo izomorfne normirane prostore in produkt (ali direktna vsota ) je poln, če in samo če sta oba faktorja polna.
Če je zaprti linearni podprostor normiranega prostora , obstaja naravna norma na kvocientnem prostoru :
Kvocient je Banachov prostor, kadar je poln.[17]:17–19 Kvocientna preslikava iz na , ki preslikuje v njegov razred , je linearna in ima normo enako , razen kadar je , ko je kvocient ničelni prostor.
Zaprti linearni podprostor od se imenuje komplementni podprostor od , če je območje surjektivne omejene linearne projekcije . V tem primeru je prostor izomorfen direktni vsoti in , jedra projekcije .
Naj sta in Banachova prostora in naj je . Potem obstaja kanonična faktorizacija od kot:[17]:17–19
kjer je prva preslikava kvocientna preslikava, druga pa preslikuje vsak razred v kvocientu na sliko v . To je dobro definirano, ker imajo vsi elementi v istem razredu enako sliko. Preslikava je linearna bijekcija iz na območje , katere inverz mora biti omejen.
Klasični prostori[uredi | uredi kodo]
Med osnovne zglede[16]:11–12 Banachovih prostorov spadajo: prostori Lp in njihovi posebni primeri, prostori zaporedij , ki jih sestavljajo skalarna zaporedja, indeksirana z naravnimi števili – med njimi prostor absolutno sumabilnih zaporedij in prostor kvadratno sumabilnih zaporedij; prostor zaporedij, ki težijo k ničli, in prostor omejenih zaporedij; prostor zveznih skalarnih funkcij kompaktnega Hausdorffovega prostora , opremljenega z največjo normo:
Po Banach-Mazurjevem izreku je vsak Banachov prostor izometrično izomorfen podprostoru nekega prostora .[18] Za vsak separabilni Banachov prostor obstaja takšen zaprti podprostor od , da je .[19]
Vsak Hilbertov prostor služi kot zgled Banachovega prostora. Hilbertov prostor na je poln za normo oblike:
kjer je:
skalarni produkt, linearen v svojem prvem argumentu, za katerega velja naslednje:
Prostor je na primer Hilbertov prostor.
Hardyjev prostor in prostor Soboljeva sta zgleda Banachovih prostorov, ki sta povezana s prostori in imata dodatno strukturo. Med drugim sta pomembna v različnih vejah matematične analize, harmonične analize in parcialnih diferencialnih enačbah.
Banachove algebre[uredi | uredi kodo]
Banachova algebra je Banachov prostor nad ali , skupaj s takšno strukturo algebre na , da je produktna preslikava zvezna. Ekvivalentna norma na se lahko najde, tako da velja za vse .
Zgledi[uredi | uredi kodo]
- Banachov prostor s točkovnim produktom je Banachova algebra.
- algebro diskov sestavljajo funkcije, holomorfne na odprtem enotskem disku in zveznem na svoji zapolnitvi: . Opremljena z največjo normo na , je algebra diskov zaprta podalgebra od .
- Wienerjeva algebra je algebra funkcij na enotski krožnici z absolutno konvergentnimi Fourierovimi vrstami. Preko preslikave, ki povezuje funkcijo na z zaporedjem njenih Fourierovih koeficientov, je ta algebra izomorfna Banachovi algebri , kjer je produkt konvolucija zaporedij.
- za vsak Banachov prostor je prostor omejenih linearnih operatorjev na s kompozicijo preslikav kot produktom Banachova algebra.
- C*-algebra je kompleksna Banachova algebra s takšno antilinerno involucijo , da je . Prostor omejenih linearnih operatorjev na Hilbertovem prostoru je osnovni zgled C*-algebre. Gelfand-Najmarkov izrek pravi, da je vsaka C*-algebra izometrično izomorfna C*-podalgebri nekega . Prostor kompleksnih zveznih funkcij na kompaktnem Hausdorffovem prostoru je zgled komutativne C*-algebre, kjer je involucija, povezana z vsako funkcijo , njen kompleksni konjugat .
Dualni prostor[uredi | uredi kodo]
Če je normirani prostor in osnovno polje (ali realnih ali kompleksnih števil), je zvezni dualni prostor prostor zveznih linearnih preslikav iz na ali zveznih linearnih funkcionalov. V tem članku je zapis za zvezni dual .[20] Ker je Banachov prostor, (ki ima za normo absolutno vrednost), je dual banachov prostor za vsak normirani prostor . Dixmier-Ngov izrek karakterizira dualne prostore Banachovih prostorov.
Glavno orodje za dokazovanje obstoja zveznih linearnih funkcionalov je Hahn-Banachov izrek.
Hahn-Banachov izrek: Naj je vektorski prostor nad poljem . Naj je naprej
- linearni podprostor,
- podlinearna funkcija in
- takšen linearni funkcional, da velja za vse .
Potem obstaja takšen linearni funkcional , da velja:
Še posebej, vsak zvezni linearni funkcional na podprostoru normiranega prostora je mogoče zvezno razširiti na celoten prostor, ne da bi se povečalo normo funkcionala.[21] Pomemben poseben primer je naslednji: za vsak vektor v normiranem prostoru obstaja takšen zvezni linearni funkcional na , da je:
Kadar ni enak vektorju , mora imeti funkcional normo enako , in se imenuje normirajoči funkcional za .
Hahn-Banachov separacijski izrek pravi, da se lahko dve nepovezani neprazni konveksni množici v realnem Banachovem prostoru, od katerih je ena odprta, ločita z zaprto afino hiperravnino. Odprta konveksna množica leži strogo na eni strani hiperravnine, druga konveksna množica pa leži na drugi strani, vendar se lahko dotika hiperravnine.[22]
Podmnožica v Banachovem prostoru je totalna, če je linearna ogrinjača gosta v . Podmožica je totalna v , če in samo če je edini zvezni linearni funkcional, ki izgine na , funkcional – ta ekvivalenca sledi iz Hahn-Banachovega izreka.
Če je direktna vsota dveh zaprtih linearnih podprostorov in , potem je dual prostora izomorfen direktni vsoti dualov in .[17]:19 Če je zaprti linearni prostor v , ga je možno povezati z ortogonalnim v dualu:
Ortogonalni je zaprti linearni podprostor duala. Dual je izometrično izomorfen . Dual je izometrično izomorfen .[23]
Dual separabilnega Banachovega prostora ni treba, da je separabilen, vendar velja naslednji izrek:
Izrek:[24] Naj je normirani prostor. Če je separabilen, je separabilen .
Kadar je separabilen, se lahko zgornji kriterij za totalnost uporabi za dokazovanje obstoja števne totalne podmnožice v .
Šibke topologije[uredi | uredi kodo]
Šibka topologija na Banachovem prostoru je najbolj groba topologija na za katero so vsi elementi v zveznem dualnem prostoru zvezni. Normna topologija je tako bolj fina od šibke topologije. Iz Hahn-Banachoveha separacijskega izreka sledi, da je šibka topologija Hausdorffova in, da je z normo zaprta konveksna podmnožica Banachovega prostora tudi šibko zaprta.[25] Z normo zvezna linearna preslikava med dvema Banachovima prostoroma in je tudi šibko zvezna, kar pomeni, da je zvezna iz šibke topologije od k tisti od .[26]
Če je neskončnorazsežen, obstajajo linearne preslikave, ki niso zvezne. Prostor vseh linearnih preslikav iz na osnovno polje , (ta prostor se imenuje algebrski dualni prostor, da se ga razlikuje od ), tudi inducira topologijo na , ki je bolj fina od šibke topologije in se v funkcionalni analizi rabi manj.
Na dualnem prostoru obstaja topologija, ki je šibkejša od šibke topologije , imenovana šibka* topologija. Je najbolj groba topologija na za katero so vse evaluacijske preslikave , kjer teče čez ves , zvezne. Njena pomembnost izhaja iz Banach-Alaoglujevega izreka.
Banach-Alaoglujev izrek: Naj je normirani vektorski prostor. Potem je zaprta enotska krogla dualnega prostora kompaktna v šibki* topologiji.
Banach-Alaoglujev izrek se lahko dokaže s pomočjo izreka Tihonova o neskončnih produktih kompaktnih Hausdorffovih prostorov. Kadar je separabilen, je enotska krogla duala metrizabilno kompaktna v šibki* topologiji.[27]
Zgledi dualnih prostorov[uredi | uredi kodo]
Dual je izometrično izomorfen : za vsak omejeni linearni funkcional na obstaja takšen edinstven element , da velja:
Dual je izometrično izomorfen . Dual Lebesguovega prostora je izometrično izomorfen , kadar je in .
Za vsak vektor v Hilbertovem prostoru preslikava:
definira zvezni linearni funkcional na . Rieszev reprezentacijski izrek pravi, da ima vsak zvezni linearni funkcional na obliko za edinstveno definiran vektor v . Preslikava je antilinearna izometrična bijekcija iz na svoj dual . Kadar so skalarji realni, je takšna preslikava izometrični izomorfizem.
Kadar je kompaktni Hausdorffov topološki prostor, je dual od prostor Radonovih mer v Bourbakijevem smislu.[28] Podmnožica od , ki jo sestavljajo nenegativne mere z maso enako (mere verjetnosti), je konveksna w*-zaprta podmnožica enotske krogle . Ekstremne točke so Diracove mere na . Množica Diracovih mer na , opremljena z w*-topologijo, je homeomorfna .
Banach-Stoneov izrek: Če sta in kompaktna Hausdorffova prostora in, če sta in izometrično izomorfni, potem sta topološka prostora in homeomorfna.[29][30]
Rezultat sta razširila Dan Amir[31] in M. Cambern[32][33] na primer, ko je multiplikativna Banach-Mazurjeva razdalja med in enaka . Izrek ne velja več, ko je razdalja enaka .[34]
V komutativni Banachovi algebri so maksimalni idelai ravno jedra Diracovih mer na :
Na splošno se lahko z Gelfand-Mazurjevim izrekom maksimalne ideale unitalne komutativne Banachove algebre identificira z njenimi karakterji – ne samo kot množice, ampak kot topološke prostore: prve s topologijo jedra ogrinjače in druge z w*-topologijo. V tej identifikaciji se lahko na prostor maksimalnih idealov gleda kot na w*-kompaktno podmnožico enotske krogle v dualu .
Izrek: Če je kompaktni Hausdorffov prostor, potem je prostor maksimalnih ideaalov Banachove algebre homeomorfen .[29]
Vsaka unitalna komutativna Banachova algebra ni oblike za kakšen kompaktni Hausdorffov prostor . Ta uzjava pa velja, le se postavi v manjšo kategorijo komutativnih C*-algeber. Gelfandov reprezentacijski izrek za komutativne C*-algebre pravi, da je vsaka komutativna unitalna C*-algebra izometrično izomorfna prostoru .[35] Hausdorffov kompaktni prostor je tukaj spet prostor maksimalnih idealov, imenovan spekter v kontekstu C*-algeber.
Bidual[uredi | uredi kodo]
Če je normirani prostor, se (zvezni) dual duala imenuje bidual ali drugi dual . Za vsak normirani prostor obstaja naravna preslikava:
To definira kot zvezni linearni funkcional na , to je element . Preslikava je linearna preslikava iz na . Kot posledica obstoja normirajočega funkcionala za vsak je ta preslikava izometrična in zato injektivna.
Dual od je na primer identificiran z , dual od pa z , prostorom omejenih skalarnih zaporedij. Pod tema identifikacijama je inkluzivna preslikava iz na . Je res izometrična, vendar ne na.
Če je surjektiven, potem se normirani prostor imenuje refleksiven (glej spodaj). Ker je dual normiranega prostora, je bidual poln, in zato je vsak refleksivni normirani prostor Banachov.
Z uporabo izometrične vložitve je običajno obravnavati normirani prostor kot podmnožico njegovega biduala. Ko je Banachov prostor, se nanj gleda kot na zaprti linearni podprostor . Če ni refleksiven, je enotska krogla prava podmnožica enotske krogle . Goldstineov izrek pravi, da je enotska krogla normiranega prostora šibko*-gosta v enotski krogli biduala. Z drugimi besedami, za vsak v bidualu obstaja takšna mreža v , tako da je:
Mrežo se lahko nadomesti s šibko*-konvergentnim zaporedjem, ko je dual separabilen. Po drugi strani pa elementi biduala , ki niso v , ne morejo biti šibka*-limita zaporedij v , ker je šibko zaporedoma poln.
Banachovi izreki[uredi | uredi kodo]
Tukaj so glavni splošni rezultati o Banachovih prostorih, ki segajo v čas Banachove knjige[16], in so povezani z Baireovim izrekom o kategoriji. V skladu s tem izrekom poln metrični prostor (kot so: Banachov prostor, Fréchetov prostor ali prostor F) ne more biti enak uniji števno mnogo zaprtih podmnožic s prazno notranjostjo. Zato Banachov prostor ne more biti unija števno mnogo zaprtih podprostorov, razen če je že enak enemu izmed njih – Banachov prostor s števno Hamelovo bazo je končnorazsežen.
Banach-Steinhausov izrek: Naj je Banachov prostor in naj je normirani vektorski prostor. Naj je zbirka zveznih linearnih operatorjev iz na . Načelo uniformne omejenosti pravi, da, če za vse v velja , potem je .
Banach-Steinhausov izrek ni omejen samo na Banachove prostore. Razširi se ga lahko na primer, ko je Fréchetov prostor, pod pogojem, da se sklep spremeni na naslednji način: pod isto domnevo obstaja takšna okolica od v , tako da so vsi v uniformno omejeni na :
Izrek o odprti preslikavi: Naj sta in Banachova prostora in naj je surjektivni zvezni linearni operator. Potem je odprta preslikava.
Posledica: Vsak ena proti ena omejeni linearni operator iz Banachovega prostora v Banachov prostor je izomorfizem.
Prvi izrek o izomorfizmu za Banachove prostore: Naj sta in Banachova prostora in naj je . Naj je naprej območje zaprto v . Potem je izomorfen .
Ta rezultat je neposredna posledica prejšnjega Banachovega izreka o izomorfizmu in kanonične faktorizacije omejenih linearnih preslikav.
Posledica: Če je Banachov prostor notranja direktna vsota zaprtih prostorov , potem je izomorfen
To je še ena posledica Banachovega izreka o izomorfizmu, uporabljenega za zvezno bijekcijo iz na , ki pošilja v vsoto .
Izrek o zaprtem grafu: Naj je linearna preslikava med Banachovima prostoroma. Graf je zaprt v , če in samo če je zvezna.
Refleksivnost[uredi | uredi kodo]
Normirani prostor se imenuje refleksiven, kadar je naravna preslikava:
surjektivna. Refleksivni normirani prostori so Banachovi.
Izrek: Če je refleksivni Banachov prostor, sta vsak zaprti podprostor in vsak kvocientni prostor refleksivna.
To je posledica Hahn-Banachovega izreka. Nadalje, po izreku o odprti preslikavi, če obstaja omejeni linearni operator iz Banachovega prostora v Banachov prostor , potem je refleksiven.
Izrek: Če je Banachov prostor, potem je refleksiven, če in samo če je reflesiven .
Posledica: Naj je refleksivni Banachov prostor. Potem je separabilen, če in samo če je separabilen .
Res, če je dual Banachovega prostora separabilen, potem je separabilen . Če je refleksiven in separabilen, potem je separabilen dual , in je tako separabilen .
Izrek: Naj so normirani prostori in naj je . Potem je refleksiven, če in samo če je refleksiven vsak od .
Hilbertovi prostori so refleksivni. Prostori so refleksivni kadar je . Bolj splošno so uniformno konveksni prostori refleksivni po Milman-Pettisovem izreku. Prostori: niso refleksivni. V teh primerih nerefleksivnih prostorov je bidual »veliko večji« od . Namreč, pod naravno izometrično vložitvijo na je po Hahn-Banachovem izreku kvoicient neskončnorazsežen in celo neseparabilen. Vendar je Robert Clarke James skonstruiral takšen primer[36] nerefleksivnega prostora, po navadi imenovanega »Jamesov prostor« in označenega z ,[37]:25 da je kvocient enorazsežen. Takšen prostor je še naprej izometrično izomorfen svojemu bidualu.
Izrek: Banachov prostor je refleksiven, če in samo če je njegova enotska krogla kompaktna v šibki topologiji.
Kadar je refleksiven, sledi, da so vse zaprte in omejene konveksne podmnožice od šibko kompaktne. V Hilbertovem prostoru se šibka kompaktnost enotske krogle velikokrat rabi na naslednji način – vsako omejeno zaporedje v ima šibko konvergentna podzaporedja.
Šibka kompaktnost enotske krogle zagotavlja orodje za iskanje rešitev refleksivnih prostorov v določenih optimizacijskih problemih. Vsaka konveksna zvezna funkcija na enotski krogli refleksivnega prostora na primer doseže svoj minimum na neki točki v .
Kot poseben primer prejšnjega rezultata, ko je refleksivni prostor nad , vsak zvezni linearni funkcional v doseže svoj maksimum na enotski krogli . Naslednji Jamesov izrek zagotavlja obratno izjavo.
Jamesov izrek: Za Banachov prostor veljata naslednji dve enakovredni značilnosti:
- je refleksiven.
- za vse v obstaja takšen z , tako da je .
Izrek je mogoče razširiti, da poda karakterizacijo šibko kompaktnih konveksnih množic.
Na vsakem nerefleksivnem Banachovem prostoru obstajajo zvezni linearni funkcionali, ki ne dosegajo norme. Vendar Bishop-Phelpsov izrek[38] pravi, da so funkcionali, ki dosegajo normo, normno gosti v dualu od .
Šibke konvergence zaporedij[uredi | uredi kodo]
Zaporedje v Banachovem prostoru je šibko konvergentno k vektorju , če konvergira k za vsak zvezni linearni funkcional v dualu . Zaporedje je šibko Cauchyjevo zaporedje, če konvergira k skalarni limiti za vsak v . Zaporedje v dualu je šibko* konvergentno k funkcionalu , če konvergira k za vsak v . Šibka Cauchyjeva zaporedja, šibko konvergentna in šibko* konvergentna zaporedja so normno omejena, kar je posledica Banach-Steinhausovega izreka.
Kadar je zaporedje v šibko Cauchyjevo, limita zgoraj definira omejeni linearni funkcional na dualu to je, element biduala od in je limita od v šibki*-topologiji biduala. Banachov prostor je šibko zaporedoma poln, če je vsako šibko Cauchyjevo zaporedje šibko konvergentno v . Iz predhodne razprave sledi, da so refleksivni prostori šibko zaporedoma polni.
Izrek:[39] Za vsako mero je prostor šibko zaporedoma poln.
Ortonormirano zaporedje v Hilbertovem prostoru je preprosti zgled šibko konvergentnega zaporedja, z limito enako vektorju . Baza enotskega vektorja od za ali od je naslednji zgled šibko ničelnega zaporedja, zaporedja, ki konvergira šibko k . Za vsako šibko ničelno zaporedje v Banachovem prostoru obstaja zaporedje konveksnih kombinacij vektorjev iz danega zaporedja, ki normno konvergira k .[40]
Baza enotskega vektorja od ni šibko Cauchyjeva. Šibko Cauchyjeva zaporedja v so šibko konvergentna, ker so prostori šibko zaporedoma polni. Dejansko so šibko konvergentna zaporedja v normno konvergentna.[41]:85 To pomeni, da za velja Schurova značilnost.
Rezultati, ki vključujejo bazo [uredi | uredi kodo]
Šibko Cauchyjeva zaporedja in baza so nasprotni zgledi dihotomije, vzpostavljene v naslednjem globokem rezultatu Haskella P. Rosenthala.[42] Rosenthalov dokaz velja za realne skalarje. Kompleksno različico rezultata je podal Leonard E. Dor.[43]
Izrek:[41]:201 Naj je omejeno zaporedje v Banachovem prostoru. ima bodisi šibko Cauchyjevo zaporedje, ali pa dopušča šibko zaporedje, enakovredno standardni bazi enotskega vektorja od .
Dopolnilo k temu rezultatu sta podala Odell in Rosenthal.[44]
Izrek: Naj je separabilni Banachov prostor. Naslednje je enakovredno:
- prostor ne vsebuje zaprtega podprostora izomorfnega k .
- vsak element biduala je šibka* limita zaporedja v .
Po Goldstineovem izreku je vsak element enotske krogle od šibka* limita mreže v enotski krogli od . Kadar ne vsebuje , je vsak element od šibka* limita zaporedja v enotski krogli od .[45]
Kadar je Banachov prostor separabilen, je enotska krogla duala , opremljenega s šibko* topologijo, metrizabilno kompaktni prostor [27] in vsak element v bidualu definira omejeno funkcijo na :
Ta funkcija je zvezna za kompaktno topologijo od , če in samo če je dejansko v in velja za podmnožico od . Naj poleg tega za ves preostali razdelek velja, da ne vsebuje . Po prejšnjem rezultatu Odella in Rosenthala je funkcija točkovna limita na zaporedja zveznih funkcij na in je tako prva funkcija Bairovega razreda na . Enotska krogla biduala je točkovno kompaktna podmnožica prvega Baireovega razreda na .[46]
Zaporedja, šibka in šibka* kompaktnost[uredi | uredi kodo]
Kadar je separabilen, je enotska krogla duala šibko* kompaktna po Banach-Alaoglujevem izreku in metrizabilna za šibko* topologijo,[27] in zato ima vsako omejeno zaporedje v dualu šibko* konvergentna podzaporedja. To velja za separabilne refleksivne prostore, še bolj pa za ta primer, kot je navedeno spodaj.
Šibka topologija Banachovega prostora je metrizabilna, če in samo če je končnorazsežen.[47] Če je dual separabilen, je potem šibka topologija enotske krogle od metrizabilna. To velja še posebej za separabilne refleksivne Banachove prostore. Čeprav v splošnem šibka topologija enotske krogle ni metrizabilna, se lahko karakterizira šibko kompaktnost s pomočjo zaporedij.
Eberlein-Šmuljanov izrek:[48] Množica v Banachovem prostoru je relativno šibko kompaktna, če in samo če ima vsako zaporedje v šibko konvergentno podzaporedje.
Banachov prostor je refleksiven, če in samo če ima vsako omejeno zaporedje v šibko konvergentno podzaporedje.[49]
Šibko kompaktna podmnožica v je normno kompaktna. Res ima vsako zaporedje v šibko konvergentna podzaporedja po Eberlein-Šmuljanovem izreku, ki so normno konvergentna po Schurovi značilnosti od .
Tip in kotip[uredi | uredi kodo]
Način za klasifikacijo Banachovih prostorov je s pomočjo verjetnostnega pojma tipa in kotipa – ta dva merita, kako daleč je Banachov prostor od Hilbertovega prostora.
Schauderjeve baze[uredi | uredi kodo]
Schauderjeva baza v Banachovem prostoru je zaporedje vektorjev v z značilnostjo, da za vsak vektor obstajajo takšni edinstveno definirani sklarji , odvisni od , da je:
Banachovi prostori s Schauderjevo bazo so nujno separabilni, ker števna množica končnih linearnih kompinacij z racionalnimi koedicienti je, (recimo), gosta.
Iz Banach-Steinhausovega izreka sledi, da so linearne preslikave uniformno omejene z neko konstanto . Naj označuje koordinatne funkcionale, ki vsakemu v priredijo koordinate od v zgornjem izrazu. Imenujejo se biortogonalni funkcionali. Kadar ima baza vektorjev normo enako , imajo koordinatni funkcionali norme enake v dualu od .
Večina klasičnih separabilnih prostorov ima eksplicitne baze. Haarov sistem je baza za . Trigonometrični sistem je baza v pri . Schauderjev sistem je baza v prostoru .[37]:3 Vprašanje ali ima algebra diskov bazo[50] je ostalo odprto več kot štirideset let dokler Sergej Viktorovič Bočkarjov leta 1974 ni pokazal, da dovoljuje bazo skonstruirano iz Franklinovega sistema.[51]
Ker je vsak vektor v Banachovem prostoru z bazo limita od , kjer ima končni rang in je uniformno omejena, za vsak prostor velja omejena aproksimacijska značilnost. Prvi primer Pera Enfloja prostora za katerega aproksimacijska značilnost ne velja je bil istočasno prvi primer separabilnega Banachovega prostora brez Schauderjeve baze.[52]
James je karakteriziral refleksivnost v Banachovih prostorih z bazo: prostor s Schauderjevo bazo je refleksiven, če in samo če je baza skrčajoča in omejeno polna.[53][37]:9 V tem primeru biortogonalni funkcionali tvorijo bazo duala .
Tenzorski produkt[uredi | uredi kodo]
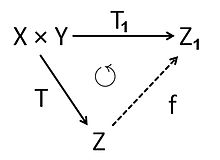
Naj sta in dva -vektorska prostora. Tenzorski produkt od in je -vektorski prostor z bilinearno preslikavo , ki ima naslednjo univerzalno značilnost:
- Če je poljubna bilinearna preslikava na -vektorski prostor , potem obstaja takšna edinstvena linearna preslikava , da je .
Slika pod para v je označena z in se imenuje enostavni tenzor. Vsak element v je končna vsota takšnih enostavnih tenzorjev.
Obstajajo različne norme, ki jih je mogoče postaviti na tenzorski produkt osnovnih vektorskih prostorov, med drugim projektivna vektorska norma in injektivna vektorska norma, ki ju je uvedel Alexander Grothendieck leta 1955.[54][55]
V splošnem tenzorski produkt polnih prostorov ni spet poln. Kadar se obravnavajo Banachovi prostori, je običajno reči, da je projektivni tenzorski produkt[56] dveh Banachovih prostorov in zapolnitev algebrskega tenzorskega produkta , opremljenega s projektivno tenzorsko normo, in podobno za injektivni tenzorski produkt.[57] Grothendieck je posebej dokazal, da velja:[58]
kjer je kompaktni Hausdorffov prostor, Banachov prostor zveznih funkcij iz na in prostor merljivih funkcij po Bochnerju in integrabilnih iz na , in kjer so izomorfizmi izometrični. Dva zgornja izomorfizma sta ustrezni razširitvi preslikave, ki pošilja tenzor k funkciji z vektorsko vrednostjo .
Tenzorski produkti in aproksimacijska značilnost[uredi | uredi kodo]
Naj je Banachov prostor. Tenzorski produkt je identificiran izometrično z zaprtjem v množice operatorjev s končnim rangom. Kadar ima aproksimacijsko značilnost, to zaprtje sovpada s prostorom kompaktnih operatorjev na .
Za vsak Banahov prostor obstaja linearna preslikava z naravno normo enako :
ki se jo dobi z razširitvijo identične preslikave algebrskega tenzorskega produkta. Grothendieck je povezal aproksimacijsko značilnost z vprašanjem, ali je ta preslikava ena na ena, ko je dual . Natančneje, za vsak Banachov prostor je preslikava:
injektivna, če in samo če ima aproksimacijsko značilnost.[59]
Grothendieck je domneval, da morata biti in različni kadar sta in neskončnorazsežna Banachova prostora. To je ovrgel Gilles Pisier leta 1983.[60] Pisier je skonstruiral takšen neskončnorazsežen Banachov prostor , da sta in enaki. Kakor pri Enflojevem primeru je naprej ta prostor »narejen na roke« in nima aproksimacijske značilnosti. Na drugi strani je Andrzej Szankowski dokazal, da klasični prostor nima aproksimacijske značilnosti.[61][62]
Nekateri klasifikacijski rezultati[uredi | uredi kodo]
Karakterizacija Hilbertovega prostora med Banachovimi prostori[uredi | uredi kodo]
Potreben in zadosten pogoj, da je norma Banachovega prostora povezana z notranjim produktom, je paralelogramska enakost:
Paralelogramska enakost: za vse
Iz tega na primer sledi, da je Lebesguov prostor Hilbertov le, če je . Če je ta enakost izpolnjena, je povezani notranji produkt podan s polarizacijsko enakostjo. V primeru realnih skalarjev to da:
Za kompleksne skalarje, kjer se skalarni produkt definira tako, da je -linearen v in antilinearen v , polarizacijska enakost da:
Da se ugotovi ali zakon paralelograma zadostuje, se v realnem primeru opazi, da je simetričen, v kompleksnem primeru pa, da izpolnjuje značilnost hermitske simetrije in . Zakon paralelograma implicira, da je aditiven v . Iz tega sledi, da je linearen nad racionalnimi števili, torej linearen po zveznosti.
Na voljo je več karakterizacij prostorov, ki so izomorfni (namesto izometrični) Hilbertovim prostorom. Zakon paralelograma je mogoče razširiti na več kot dva vektorja in oslabiti z uvedbo dvostranske neenakosti s konstanto : Stanisław Kwapień je dokazal, da če je:
za vsako celo število in vse družine vektorjev , potem je Banachov prostor izomorfen Hilbertovem.[63] Tukaj označuje srednjo vrednost nad možnimi izbirami predznakov . V istem članku je Kwapień dokazal, da veljavnost Parsevalovega izreka z Banachovo vrednostjo za Fourierovo transformacijo kakarkterizira Banachove prostore izomorfne Hilbertovim.
Joram Lindenstrauss in Lior Tzafriri sta dokazala, da je Banachov prostor, v katerem je vsak zaprt linearni podprostor komplementiran (to je območje omejene linearne projekcije), izomorfen Hilbertovemu prostoru.[64] Dokaz se naslanja na izrek Dvoretzkega o evklidskih presekih večrazsežnih centralno simetričnih konveksnih teles. Z drugimi besedami, izrek Dvoretzkega pravi, da za vsako celo število vsak končnorazsežni normirani prostor z dovolj veliko razsežnostjo v primerjavi z vsebuje podprostore skoraj izometrične glede na -razsežni evklidski prostor.
Naslednji rezultat daje rešitev tako imenovanega problema homogenega prostora. Neskončnorazsežni Banachov prostor je homogen, če je izomorfen vsem svojim neskončnorazsežnim zaprtim podprostorom. Banachov prostor, izomorfen , je homogen in Banach se je vprašal obratno.[16]:245 Značilnost homogenosti se tam imenuje »propriété (15)«. Banach je zapisal: »on ne connaît aucun exemple d'espace à une infinité de dimensions qui, sans être isomorphe avec . possède la propriété (15)«.[m]
Izrek:[65] Banachov prostor izomorfen vsem svojim neskončnorazsežnim zaprtim podprostorom je izomorfen separabilnemu Hilbertovemu prostoru.
Neskončnorazsežni Banachov prostor je dedno nedekompozabilen, če noben njegov podprostor ne more biti izomorfen direktni vsoti dveh neskončnorazsežnih Banachovih prostorov. Gowersov izrek o dihotomiji[65] pravi, da vsak neskončnorazsežni Banachov prostor vsebuje bodisi podprostor z brezpogojno bazo, ali dedno nedekompozabilni podprostor , ter še posebej ni izomorfen svojim zaprtim hiperravninam.[66] Če je homogen, mora zato imeti brezpogojno bazo. Nato izhaja iz delne rešitve, ki sta jo pridobila Ryszard A. Komorowski in Nicole Tomczak-Jaegermann za prostore z brezpogojno bazo, [67][68], da je izomorfen .
Metrična klasifikacija[uredi | uredi kodo]
Če je izometrija iz Banachovega prostora na Banachov prostor , (kjer sta oba in vektorska prostora nad ), potem Mazur-Ulamov izrek pravi, da mora biti afina transformacija. Še posebej, če je , to je preslikuje ničlo od na ničlo od , potem mora biti linearna. Ta rezultat implicira, da metrika v Banachovem prostoru in na splošno v normiranih prostorih popolnoma zajame njihovo linearno strukturo.
Topološka klasifikacija[uredi | uredi kodo]
Končnorazsežni Banachovi prostori so homeomorfni kot topološki prostori, če in samo če imajo isto razsežnost kot vektorski prostori.
Anderson-Kadecov izrek (1965–66) dokazuje,[69] da sta poljubna neskončnorazsežna separabilna Banachova prostora homeomorfna kot topološka prostora. Kadecov izrek je razširil H. Torunczyk, ki je dokazal,[70] da sta poljubna Banachova prostora homeomorfna, če in samo če imata enak karakter gostote, najmanjšo kardinalnost goste podmožice.
Prostori zveznih funkcij[uredi | uredi kodo]
Kadar sta kompaktna Hausdorffova prostora in homeomorfna, sta Banachova prostora in izometrična. Obratno, kadar ni homeomorfen , mora biti (multiplikativna) Banach-Mazurjeva razdalja med in večja ali enaka od , (glej zgoraj rezultate Amirja in Camberna). Čeprav imajo neštevni kompaktni metrični prostori lahko različne homeomorfne tipe, velja naslednji Milyutinov rezultat:[71]
Razmere so različne za števno neskončne kompaktne Hausdorffove prostore. Vsak števno neskončni kompaktni je homeomorfen nekemu zaprtemu intervalu ordinalnih števil:
opremljenemu s topologijo urejenosti, kjer je števno neskočni ordinal.[73] Banachov prostor je nato izometričen k . Kadar sta števno neskončna ordinala, in, če se privzame , sta prostora in izomorfna, če in samo če je .[74] Banachovi prostori:
na primer med seboj niso izomorfni.
Zgledi[uredi | uredi kodo]
Glosar simbolov za spodnjo razpredelnico:
- – polje realnih števil ali kompleksnih števil ,
- – kompaktni Hausdorffov prostor,
- – realna števila z , ki so Hölderjevi konjugati, kar pomeni, da za njih velja in tako tudi ,
- – -algebra množic,
- – algebra množic (za prostore se zahteva le končna aditivnost, kot je na primer prostor ba),
- – mera z variacijo . Pozitivna mera je funkcija množice z realnimi vrednostmi, definirana na -algebri, ki je števno aditivna.
| klasični Banachovi prostori | ||||||
| dualni prostor | refleksivni | šibko zaporedoma polni | norma | opombe | ||
|---|---|---|---|---|---|---|
| Da | Da | evklidski prostor | ||||
| Da | Da | |||||
| Da | Da | |||||
| Da | Da | |||||
| Ne | Da | |||||
| Ne | Ne | |||||
| Ne | Ne | |||||
| Ne | Ne | izomorfen vendar ne izometričen | ||||
| Ne | Da | izometrično izomorfen | ||||
| Ne | Da | izometrično izomorfen | ||||
| Ne | Ne | izometrično izomorfen | ||||
| Ne | Ne | izometrično izomorfen | ||||
| Ne | Ne | |||||
| Ne | Ne | |||||
| ? | Ne | Da | ||||
| ? | Ne | Da | zaprti podprostor | |||
| ? | Ne | Da | zaprti podprostor | |||
| Da | Da | |||||
| Ne | Da | dual je , če je -končna | ||||
| ? | Ne | Da | je totalna variacija od | |||
| ? | Ne | Da | sestavljajo takšne funkcije , da je | |||
| Ne | Da | izomorfen prostoru Soboljeva | ||||
| Ne | Ne | izomorfen v bistvu po Taylorjevem izreku | ||||
Odvodi[uredi | uredi kodo]
Na Banachovem prostoru je mogoče definirati več konceptov odvoda. Za podrobnosti glej članka o Fréchetovem odvodu in Gateauxjevem odvodu. Fréchetov odvod omogoča razširitev koncepta totalnega odvoda na Banachove prostore. Gateauxjev odvod omogoča razširitev smernega odvoda na krajevno konveksne topološke vektorske prostore. Fréchetova diferenciabilnost je močnejši pogoj kot Gateauxjeva diferenciabilnost. Kvaziodvod je še ena posplošitev smernega odvoda, ki implicira močnejši pogoj kot Gateauxjeva diferenciabilnost, a šibkejši pogoj kot Fréchetova diferenciabilnost.
Posplošitve[uredi | uredi kodo]
Več pomembnih prostorov v funkcionalni analizi, na primer prostor vseh neskončno pogosto diferenciabilnih funkcij ali prostor vseh porazdelitev na sta polna, vendar nista normirana vektorska prostora in zato nista Banachova prostora. V Fréchetovem prostoru je še vedno polna metrika, medtem ko so LF-prostori polni uniformni vektorski prostori, ki nastanejo kot limite Fréchetovih prostorov.
Glej tudi[uredi | uredi kodo]
Opombe[uredi | uredi kodo]
- ↑ Običajno se prebere » je normirani prostor« namesto tehnično pravilnejšega vendar (po navadi) pedantnega » je normirani prostor», še posebej, če je norma dobro znana (na primer takšna s prostori ) ali kadar ni posebne potrebe po izbiri katere koli (enakovredne) norme nad katero koli drugo (zlasti v bolj abstraktni teoriji topoloških vektorskih prostorov), v kateri se ta norma (če je potrebna) pogosto samodejno predpostavi, da je označena z . Vendar pa se v situacijah, ko je poudarek na normi, običajno vidi zapisano namesto . Tehnično pravilna definicija normiranih prostorov kot parov lahko postane pomembna tudi v kontekstu teorije kategorij, kjer je običajno pomembno razlikovanje med kategorijami normiranih prostorov, normirajočih prostorov, metričnih prostorov, topoloških vektorskih prostorov, topoloških prostorov itd.
- ↑ To pomeni, da če se norma nadomesti z drugo normo na , potem ni enako normiran prostor kot , niti če so norme enakovredne. Vendar pa enakovrednost norm na danem vektorskem prostoru tvori ekvivalenčno relacijo.
- ↑ 3,0 3,1 3,2 Metrika v vektorskem prostoru naj bi bila translacijsko invariantna, če velja za vse vektorje . To se zgodi, če in samo če je za vse vektorje . Metrika, ki jo inducira norma, je vedno translacijsko invariantna.
- ↑ Ker je za vse , vedno velja, da je za vse . Tako red in v tej definiciji nista pomembna.
- ↑ 5,0 5,1 Naj je separabilni Hilbertov prostor kvadratno sumabilnih zaporedij z običajno normo in naj je standardna ortonormalna baza, (ki je enaka v koordinati). Zaprta množica je kompaktna, (ker je zaporedoma kompaktna), vendar njena konveksna ogrinjača ni zaprta množica, ker pripada zaprtju v , vendar , (ker je vsako zaporedje končna konveksna kombinacija elementov in tako je enako za vse, vendar za končno mnogo koordinat, kar ne velja za ). Vendar kot v vseh polnih Hausdorffovih krajevno konveksnih prostorih je zaprta konveksna ogrinjača te kompaktne podmožice kompaktna. Vektorski podprostor je prehilbertov prostor, ko je opremljen s podstrukturo da jo Hilbertov prostor inducira nanj, vendar ni poln in , (ker ). Zaprta konveksna ogrinjača v (tu »zaprta« pomeni glede na in ne glede na kot prej) je enaka , ki ni kompaktna, (ker ni polna podmnožica). To kaže, da v Hausdorffovem krajevno konveksnem prostoru, ki ni poln, zaprta konveksna ogrinjača kompaktne podmnožice morda ne bo kompaktna, (čeprav bo prekompaktna/popolnoma omejena).
- ↑ Naj označuje Banachov prostor zveznih funkcij z največjo normo in naj označuje topologijo na , ki jo inducira . Vektorski prostor se lahko identificira (prek inkluzivne preslikave) kot pravi gosti vektorski podprostor prostora , za katerega velja za vse . Naj označuje omejitev norme na , ki naredi to preslikavo normo na (v splošnem bo omejitev poljubne norme na poljubni vektorski podprostor nujno spet norma). Normirani prostor ni Banachov prostor, ker je njegova zapolnitev prava supermnožica . Ker velja na , je preslikava zvezna. Navkljub temu norma ni ekvivalentna normi , (ker je polna, vendar ni).
- ↑ Normirani prostor je Banachov prostor kjer je absolutna vrednost norma na realni premici , ki inducira običajno evklidsko topologijo na . Naj je definirana metrika na z za vse . Kakor inducirana metrika , tudi metrika inducira običajno evklidsko topologijo na . Vendar ni polna metrika, ker je zaporedje , definirano z , -Cauchyjevo zaporedje, vendar ne konvergira k nobeni točki na . Kot posledica nekonvergence to -Cauchyjevo zaporedje ne more biti Cauchyjevo zaporedje v , (to je, da ni Cauchyjevo zaporedje glede na normo ), ker če bi bilo -Cauchyjevo, bi iz dejstva, da je Banachov prostor, izhajalo da konvergira, (kar je protislovje).[2]:47–51
- ↑ V izreku naj je takšna poljubna metrika na vektorskem prostoru , da topologija , ki jo inducira na naredi topološki vektorski prostor. Če je polni vektorski prostor, potem je polni topološki vektorski prostor.
- ↑ Ta metrika ni privzeto translacijsko invariantna. Tako še posebej ni nujno inducirana z normo.
- ↑ Norma (ali polnorma) na topološkem vektorskem prostoru je zvezna, če in samo če je topologija ki jo inducira na , bolj groba kot , (kar pomeni ). To se zgodi, če in samo če obstaja takšna poljubna krogla v (da je na primer mogoče ), ki je odprta v .
- ↑ označuje zvezni dualni prostor . Kadar je opremljen s topologijo močnega dualnega prostora, imenovano tudi topologija uniformne konvergence na omejenih podmnožicah , je to naznačeno z zapisom , (včasih se rabi spodnji indeks namesto ). Kadar je normirani prostor z normo , potem je ta topologija enaka topologiji na , ki jo inducira dualna norma. Na ta način je močna topologija posplošitev običajne topologije, inducirane z dualno normo na .
- ↑ Dejstvo, da je odprta, kar nakazuje, da je zvezna, poenostavlja dokazovanje zveznosti, ker to pomeni, da je dovolj pokazati, da je odprta za in v (kjer je ), namesto da se pokaže to za vse realne in vse .
- ↑ »ne poznamo nobenega primera prostora z neskončnimi razsežnostmi, ki ima, ne da bi bil izomorfen z značilnost (15)«.
Sklici[uredi | uredi kodo]
- ↑ Bourbaki (1987), V.87.
- ↑ 2,0 2,1 2,2 2,3 2,4 2,5 Narici & Beckenstein (2011).
- ↑ Megginson (1998), Izrek 1.3.9, str. 20.
- ↑ Wilansky (2013), str. 29.
- ↑ Bessaga & Pełczyński (1975), str. 189.
- ↑ 6,0 6,1 Anderson & Schori (1969), str. 315.
- ↑ Henderson (1969).
- ↑ Aliprantis & Border (2006), str. 185.
- ↑ 9,0 9,1 9,2 9,3 Trèves (2006).
- ↑ 10,0 10,1 Conrad, Keith. »Equivalence of norms« (PDF). kconrad.math.uconn.edu (v angleščini). Arhivirano (PDF) iz spletišča dne 9. oktobra 2022. Pridobljeno 7. septembra 2020.
- ↑ Megginson (1998), Posledica 1.4.18, str. 32.
- ↑ Schaefer & Wolff (1999), str. 35.
- ↑ Klee (1952).
- ↑ Gabriyelyan & Ka̧kol (2015).
- ↑ 15,0 15,1 Yuan (2012).
- ↑ 16,0 16,1 16,2 16,3 Banach (1932).
- ↑ 17,0 17,1 17,2 Carothers (2005).
- ↑ Banach (1932), Izrek 9, str. 185.
- ↑ Carothers (2005), Izrek 6.1, str. 55.
- ↑ Več knjig o funkcionalni analizi rabi zapis za zvezni dual, na primer: Carothers (2005), Lindenstrauss & Tzafriri (1977), Megginson (1998), Ryan (2002), Wojtaszczyk (1991).
- ↑ Megginson (1998), Izrek 1.9.6, str. 75.
- ↑ Megginson (1998), Izrek 2.2.26, str. 179.
- ↑ Megginson (1998), Izreka 1.10.16, 1.10.17 str. 94–95.
- ↑ Megginson (1998), Izrek 1.12.11, str. 112.
- ↑ Megginson (1998), Izrek 2.5.16, str. 216.
- ↑ Wojtaszczyk (1991), II.A.8, str. 29.
- ↑ 27,0 27,1 27,2 Megginson (1998), Izrek 2.6.23, str. 231.
- ↑ Bourbaki (2004).
- ↑ 29,0 29,1 Eilenberg (1942).
- ↑ glej tudi Banach (1932), str. 170 za metrizabilna in .
- ↑ Amir (1965).
- ↑ Cambern (1966).
- ↑ Cambern (1967).
- ↑ Cohen (1975).
- ↑ Arveson (1976).
- ↑ James (1951).
- ↑ 37,0 37,1 37,2 Lindenstrauss & Tzafriri (1977).
- ↑ Bishop & Phelps (1961).
- ↑ Wojtaszczyk (1991), III.C.14, str. 140.
- ↑ Diestel (1984), Posledica 2, str. 11.
- ↑ 41,0 41,1 Diestel (1984).
- ↑ Rosenthal (1974).
- ↑ Dor (1975).
- ↑ Odell & Rosenthal (1975).
- ↑ Odell & Rosenthal (1975), Podlema str. 378 in Opomba str. 379.
- ↑ za več o točkovno kompaktnih podmnožicah Baireovega razreda glej Bourgain, Fremlin & Talagrand (1978).
- ↑ Megginson (1998), Trditev 2.5.14, str. 215.
- ↑ Wojtaszczyk (1991), str. 49, II.C.3.
- ↑ Megginson (1998), Posledica 2.8.9, str. 251.
- ↑ vprašanje se pojavi v Banachovi knjigi, Banach (1932), § 3, str. 238.
- ↑ Bočkarjov (1974).
- ↑ Enflo (1973).
- ↑ James (1950).
- ↑ Grothendieck (1955).
- ↑ Grothendieck (1953).
- ↑ Ryan (2002), § 2, str. 15.
- ↑ Ryan (2002), § 3, str. 45.
- ↑ Ryan (2002), Primer 2.19, str. 29, in str. 49–50.
- ↑ Ryan (2002), Trditev 4.6, str. 74.
- ↑ Pisier (1983).
- ↑ Szankowski (1981).
- ↑ Raymond A. Ryan trdi, da je ta razultat podal Per Enflo, Ryan (2002, str. 74).
- ↑ Kwapień (1970).
- ↑ Lindenstrauss & Tzafriri (1971).
- ↑ 65,0 65,1 Gowers (1996).
- ↑ Gowers (1994).
- ↑ Komorowski & Tomczak-Jaegermann (1995).
- ↑ Komorowski & Tomczak -Jaegermann (1998).
- ↑ Bessaga & Pełczyński (1975), str. ;177–230.
- ↑ Torunczyk (1981).
- ↑ 71,0 71,1 Milyutin (1966).
- ↑ Rosenthal (2003).
- ↑ Lahko se vzame , kjer je Cantor-Bendixsonov rang od in končno šzevilo točk v -ti izpeljani množici od . Glej Mazurkiewicz & Sierpiński (1920).
- ↑ Bessaga & Pełczyński (1960).
Viri[uredi | uredi kodo]
- Aliprantis, Charalambos Dionisios; Border, Kim C. (2006), Infinite Dimensional Analysis: A Hitchhiker's Guide (3. izd.), Berlin: Springer Science & Business Media, ISBN 978-3-540-29587-7, OCLC 262692874
- Amir, Dan (1965), »On isomorphisms of continuous function spaces«, Israel Journal of Mathematics, 3 (4): 205–210, doi:10.1007/bf03008398, S2CID 122294213
- Anderson, R. D.; Schori, R. (1969), »Factors of infinite-dimensional manifolds« (PDF), Transactions of the American Mathematical Society, Ameriško matematično društvo (AMS), 142: 315–330, doi:10.1090/s0002-9947-1969-0246327-5, ISSN 0002-9947
- Arveson, W. (1976), An Invitation to C*-Algebra, Springer-Verlag, ISBN 0-387-90176-0
- Bachman, George; Narici, Lawrence (2000), Functional Analysis (2. izd.), Mineola, New York: Dover Publications, ISBN 978-0486402512, OCLC 829157984
- Banach, Stefan (1932), Théorie des Opérations Linéaires [Theory of Linear Operations] (PDF), (Monografie Matematyczne) (v francoščini), zv. 1, Varšava: Subwencji Funduszu Kultury Narodowej, Zbl 0005.20901, arhivirano iz prvotnega spletišča (PDF) dne 11. januarja 2014, pridobljeno 11. julija 2020
- Beauzamy, Bernard (1985) [1982], Introduction to Banach Spaces and their Geometry (2. popravljena izd.), North-Holland
- Bessaga, Czesław; Pełczyński, Aleksander (1960), »Spaces of continuous functions. IV. On isomorphical classification of spaces of continuous functions«, Studia Mathematica, 19: 53–62
- Bessaga, Czesław; Pełczyński, Aleksander (1975), Selected Topics in Infinite-Dimensional Topology, (Monografie Matematyczne), Varšava: Panstwowe wyd. naukowe
- Bishop, Errett; Phelps, Robert (1961), »A proof that every Banach space is subreflexive«, Bulletin of the American Mathematical Society, 67: 97–98, doi:10.1090/s0002-9904-1961-10514-4
- Bočkarjov, Sergej Viktorovič (1974), »Existence of a basis in the space of functions analytic in the disc, and some properties of Franklin's system«, Mat. Sb. (N.S.) (v ruščini), 95(137): 3–18, 159
- Bourbaki, Nicolas (1987) [1981], Topological Vector Spaces: Chapters 1–5, (Éléments de mathématique), prevod: Eggleston, H. G.; Madan, S., Berlin; New York: Springer-Verlag, ISBN 3-540-13627-4, OCLC 17499190
- Bourbaki, Nicolas (2004), Integration I, Springer Verlag, ISBN 3-540-41129-1
- Bourgain, Jean; Fremlin, D. H.; Talagrand, Michel (1978), »Pointwise Compact Sets of Baire-Measurable Functions«, American Journal of Mathematics, 100 (4): 845–886, doi:10.2307/2373913, JSTOR 2373913
- Cambern, M. (1966), »A generalized Banach–Stone theorem«, Proceedings of the American Mathematical Society, 17 (2): 396–400, doi:10.1090/s0002-9939-1966-0196471-9
- Cambern, M. (1967), »On isomorphisms with small bound«, Proceedings of the American Mathematical Society, 18 (6): 1062–1066, doi:10.1090/s0002-9939-1967-0217580-2
- Carothers, Neal L. (2005), A short course on Banach space theory, (London Mathematical Society Student Texts), zv. 64, Cambridge: Cambridge University Press, str. xii+184, ISBN 0-521-84283-2
- Cohen, H. B. (1975), »A bound-two isomorphism between Banach spaces«, Proceedings of the American Mathematical Society, 50: 215–217, doi:10.1090/s0002-9939-1975-0380379-5
- Conway, John Bligh (1990), A course in functional analysis, (Graduate Texts in Mathematics), zv. 96 (2. izd.), New York: Springer-Verlag, ISBN 978-0-387-97245-9, OCLC 21195908
- Diestel, Joseph (1984), Sequences and series in Banach spaces, (Graduate Texts in Mathematics), zv. 92, New York: Springer-Verlag, str. xii+261, ISBN 0-387-90859-5
- Dor, Leonard E. (1975), »On sequences spanning a complex ℓ1 space«, Proceedings of the American Mathematical Society, 47: 515–516, doi:10.1090/s0002-9939-1975-0358308-x
- Dunford, Nelson; Schwartz, Jacob Theodore; with the assistance of W. G. Bade and R. G. Bartle (1958), Linear Operators. I. General Theory, (Pure and Applied Mathematics), zv. 7, New York: Interscience Publishers, Inc., MR 0117523
- Edwards, Robert Edmund (1995), Functional Analysis: Theory and Applications, New York: Dover Publications, ISBN 978-0-486-68143-6, OCLC 30593138
- Eilenberg, Samuel (1942), »Banach Space Methods in Topology«, Annals of Mathematics, 43 (3): 568–579, doi:10.2307/1968812, JSTOR 1968812
- Enflo, Per (1973), »A counterexample to the approximation property in Banach spaces«, Acta Mathematica, 130: 309–317, doi:10.1007/bf02392270, S2CID 120530273
- Gabriyelyan, Saak S.; Ka̧kol, Jerzy (1. avgust 2015), »On topological spaces and topological groups with certain local countable networks«, Topology and its Applications, 190: 59–73, arXiv:1412.1497, doi:10.1016/j.topol.2015.04.015
- Gowers, William Timothy (1994), »A solution to Banach's hyperplane problem«, Bulletin of the London Mathematical Society, 26 (6): 523–530, doi:10.1112/blms/26.6.523
- Gowers, William Timothy (1996), »A new dichotomy for Banach spaces«, Geometric and Functional Analysis, 6: 1083–1093
- Grothendieck, Alexander (1953), »Résumé de la théorie métrique des produits tensoriels topologiques«, Bol. Soc. Mat. São Paulo (8): 1–79
- Grothendieck, Alexander (1955), »Produits tensoriels topologiques et espaces nucléaires«, Memoirs of the American Mathematical Society (16): 140
- Grothendieck, Alexander (1973), Topological Vector Spaces, prevod: Chaljub, Orlando, New York: Gordon and Breach Science Publishers, ISBN 978-0-677-30020-7, OCLC 886098
- Henderson, David Wilson (1969), »Infinite-dimensional manifolds are open subsets of Hilbert space«, Bulletin of the American Mathematical Society, 75 (4): 759–762, doi:10.1090/S0002-9904-1969-12276-7, MR 0247634
- James, Robert Clarke (1950), »Bases and reflexivity of Banach spaces«, Annals of Mathematics, 52 (2): 518–527
- James, Robert Clarke (1951), »A non-reflexive Banach space isometric with its second conjugate space«, Proc. Natl. Acad. Sci. U.S.A., 37 (3): 174–177, Bibcode:1951PNAS...37..174J, doi:10.1073/pnas.37.3.174, PMC 1063327, PMID 16588998
- Khaleelulla, S. M. (1982), Counterexamples in Topological Vector Spaces, (Lecture Notes in Mathematics), zv. 936, Berlin; Heidelberg; New York: Springer-Verlag, ISBN 978-3-540-11565-6, OCLC 8588370
- Klee, Victor LaRue (1952), »Invariant metrics in groups (solution of a problem of Banach)« (PDF), Proceedings of the American Mathematical Society, 3 (3): 484–487, doi:10.1090/s0002-9939-1952-0047250-4, arhivirano (PDF) iz spletišča dne 9. oktobra 2022
- Komorowski, Ryszard A.; Tomczak-Jaegermann, Nicole (1995), »Banach spaces without local unconditional structure«, Israel Journal of Mathematics, 89 (1–3): 205–226, arXiv:math/9306211, doi:10.1007/bf02808201, S2CID 5220304
- Komorowski, Ryszard A.; Tomczak-Jaegermann, Nicole (1998), »Erratum to: Banach spaces without local unconditional structure«, Israel Journal of Mathematics, 105: 85–92, arXiv:math/9607205, doi:10.1007/bf02780323, S2CID 18565676
- Kwapień, Stanisław (1970), »A linear topological characterization of inner-product spaces«, Studia Mathematica, 38: 277–278
- Lindenstrauss, Joram; Tzafriri, Lior (1971), »On the complemented subspaces problem«, Israel Journal of Mathematics, 9 (2): 263–269, doi:10.1007/BF02771592
- Lindenstrauss, Joram; Tzafriri, Lior (1977), Classical Banach Spaces I, Sequence Spaces, (Ergebnisse der Mathematik und ihrer Grenzgebiete), zv. 92, Berlin: Springer-Verlag, ISBN 3-540-08072-4
- Mazurkiewicz, Stefan; Sierpiński, Wacław Franciszek (1920), »Contribution à la topologie des ensembles dénombrables«, Fundamenta Mathematicae, 1: 17–27
- Megginson, Robert Eugene (1998), An introduction to Banach space theory, (Graduate Texts in Mathematics), zv. 183, New York: Springer-Verlag, str. xx+596, ISBN 0-387-98431-3
- Milyutin, Alekseĭ A. (1966), »Isomorphism of the spaces of continuous functions over compact sets of the cardinality of the continuum«, Teor. Funkciĭ Funkcional. Anal. i Priložen. Vyp. (v ruščini), 2: 150–156
- Narici, Lawrence; Beckenstein, Edward (2011), Topological Vector Spaces, (Pure and applied mathematics) (2. izd.), Boca Raton, FL: CRC Press, ISBN 978-1584888666, OCLC 144216834
- Odell, Edward W.; Rosenthal, Haskell P. (1975), »A double-dual characterization of separable Banach spaces containing ℓ1« (PDF), Israel Journal of Mathematics, 20 (3–4): 375–384, doi:10.1007/bf02760341, S2CID 122391702, arhivirano (PDF) iz spletišča dne 9. oktobra 2022
- Pisier, Gilles (1983), »Counterexamples to a conjecture of Grothendieck«, Acta Mathematica, 151: 181–208
- Riesz, Frigyes; Szőkefalvi-Nagy, Béla (1990) [1955], Functional Analysis, prevod: Boron, Leo F., New York: Dover Publications, ISBN 0-486-66289-6, OCLC 21228994
- Rosenthal, Haskell P. (1974), »A characterization of Banach spaces containing ℓ1«, Proc. Natl. Acad. Sci. U.S.A., 71 (6): 2411–2413, arXiv:math.FA/9210205, Bibcode:1974PNAS...71.2411R, doi:10.1073/pnas.71.6.2411, PMC 388466, PMID 16592162
- Rosenthal, Haskell P. (2003), »The Banach spaces C(K)«, Handbook of the geometry of Banach spaces, Vol. 2, Amsterdam: North-Holland, str. 1547–1602
- Rudin, Walter (1991), Functional Analysis, (International Series in Pure and Applied Mathematics), zv. 8 (2. izd.), New York, NY: McGraw-Hill Science/Engineering/Math, ISBN 978-0-07-054236-5, OCLC 21163277
- Ryan, Raymond A. (2002), Introduction to Tensor Products of Banach Spaces, (Springer Monographs in Mathematics), London: Springer-Verlag, str. xiv+225, ISBN 1-85233-437-1
- Szankowski, Andrzej (1981), » does not have the approximation property«, Acta Mathematica, 147: 89–108
- Schaefer, Helmut Heinrich; Wolff, Manfred P. (1999), Topological Vector Spaces, (GTM), zv. 8 (2. izd.), New York, NY: Springer New York Imprint Springer, ISBN 978-1-4612-7155-0, OCLC 840278135
- Swartz, Charles (1992), An introduction to Functional Analysis, New York: M. Dekker, ISBN 978-0-8247-8643-4, OCLC 24909067
- Torunczyk, H. (1981), »Characterizing Hilbert Space Topology«, Fundamenta Mathematicae: 247–262
- Trèves, François (2006) [1967], Topological Vector Spaces, Distributions and Kernels, Mineola, N.Y.: Dover Publications, ISBN 978-0-486-45352-1, OCLC 853623322
- Wilansky, Albert (2013), Modern Methods in Topological Vector Spaces, Mineola, New York: Dover Publications, Inc, ISBN 978-0-486-49353-4, OCLC 849801114
- Wojtaszczyk, Przemysław (1991), Banach spaces for analysts, (Cambridge Studies in Advanced Mathematics), zv. 25, Cambridge: Cambridge University Press, str. xiv+382, ISBN 0-521-35618-0
- Yuan, Qiaochu (23. junij 2012), »Banach spaces (and Lawvere metrics, and closed categories)«, Annoying Precision
Zunanje povezave[uredi | uredi kodo]
- »Banach space«, Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Weisstein, Eric Wolfgang. »Banach Space«. MathWorld. (angleško)





















































































































































































![{\displaystyle L^{p}([0,1])\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3adc2738a625a3e4c60da72a5cb9ef872ca1f036)
![{\displaystyle L^{q}([0,1])\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14de40e124f7da7806b3216a5308dfffcc1b539c)











































![{\displaystyle c_{0},\ell ^{1},L^{1}([0,1]),C([0,1])\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb07506c4c0e00dd7c6b3ab887b73fa6616fa39f)
































![{\displaystyle L^{p}([0,1]),1\leq p<\infty \!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ea87d1ce325803d9eb1e653f0be1f3e61d836e6)

![{\displaystyle C([0,1])\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42d642632500787424565afb9e006b0d67690e14)













![{\displaystyle {\begin{aligned}C(K){\widehat {\otimes }}_{\varepsilon }Y&\simeq C(K,Y),\\L^{1}([0,1]){\widehat {\otimes }}_{\pi }Y&\simeq L^{1}([0,1],Y)\!\,,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc9f119acc80da2a3ea742c79bfc780a2a8d281b)

![{\displaystyle L^{1}([0,1],Y)\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2caeeb94ef82bcbfb990140d6d89420c7851023d)
![{\displaystyle [0,1]\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b26fc5fee30dada6f15cc080115cae582606d7f3)




























































































![{\displaystyle \operatorname {BV} ([a,b])\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0bc2f98e3801ab9944d4db221530486dfd9d840)

![{\displaystyle =V_{f}([a,b])+\lim \nolimits _{x\to a^{+}}f(x)\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e3f3e389e563df463aff0bef8a084b4393d6e4a)
![{\displaystyle V_{f}([a,b])\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b66b4e7e151205129f2b547a9b76843dafef2ac8)
![{\displaystyle \operatorname {NBV} ([a,b])\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4dacecc40588ffc89807104e184f822658b9298)
![{\displaystyle =V_{f}([a,b])\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff597befc1afa12aec3b7ab3cd459b1dbd350c49)

![{\displaystyle \operatorname {AC} ([a,b])\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fea029577031258852c96823680a427591d78d3)
![{\displaystyle \mathbb {F} +L^{\infty }([a,b])\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8eec628f72c81a274883a157de6f6c8668f2b6c)
![{\displaystyle W^{1,1}([a,b])\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11775d86f5fd9b44d13f17ee47b1ebb3dd25b694)
![{\displaystyle C^{n}([a,b])\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c3d6c7435774926f027f598dacecf4ca0d322d1)
![{\displaystyle \operatorname {rca} ([a,b])\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc62c41e3495ac099ddc8b5aebda7c82f6e193f9)
![{\displaystyle =\sum _{i=0}^{n}\sup \nolimits _{x\in [a,b]}\left|f^{(i)}(x)\right|\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44b26d3fe30af47cb2bceeb190dac72ca8d9c34d)
![{\displaystyle \mathbb {R} ^{n}\oplus C([a,b])\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f6ef2bdf111a68f201dfb4589fccb9c754038e1)























![{\displaystyle \left(C([0,1]),\|\cdot \|_{\infty }\right)\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6f2e30fd069babdd97bfbef18aaabe662042e35)


![{\displaystyle \left(L^{1}([0,1]),\|\cdot \|_{1}\right)\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ef142c7c0854b4687e80c2b6ff7a1914acfc682)

























