Fourierova vrsta

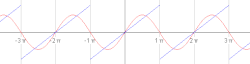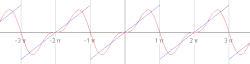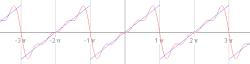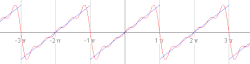
Prvi štirje približki Fourierovih vrst za pravokotni val.

Fourierove vrste v matematiki omogočajo razstavljanje poljubne periodične funkcije ali periodičnega signala v vsoto (po možnosti končno) skupine periodičnih funkcij kot sta sinus in kosinus. Proučevanje Fourierovih vrst je veja Fourierove analize.

Tako se lahko na primer funkcijo $S(x)\!\,$ razvije v neskončno vrsto po sinusih:

$S(x)=b_{1}\sin x+b_{2}\sin 2x+b_{3}\sin 3x+\cdots =\sum _{n=1}^{\infty }b_{n}\sin nx\!\,.$

Lahko pa se neko drugo funkcijo $C(x)\!\,$ razvije v neskončno vrsto po kosinusih:

$C(x)=b_{0}+b_{1}\cos x+b_{2}\cos 2x+b_{3}\cos 3x+\cdots =b_{0}+\sum _{n=1}^{\infty }b_{n}\cos nx\!\,.$

Pri tem obe funkciji ohranita nekatere osnovne značilnosti, kot so periodičnost, lihost (ali sodost), vrednost pri $x=0\!\,$ in $x=\pi \!\,$.

Imenujejo se po francoskem fiziku in matematiku Josephu Fourieru (1768–1830).

Definicija

Fourierov obrazec za periodične funkcije

Naj je periodična funkcija $f(x)\!\,$ s periodo $2\pi \!\,$, ki je integrabilna na intervalu $[-\pi ,\pi ]\!\,$. Števila:

$a_{n}={\frac {1}{\pi }}\int _{-\pi }^{\pi }f(x)\cos(nx)\,\mathrm {d} x,\quad n\geq 0\!\,$

in:

$b_{n}={\frac {1}{\pi }}\int _{-\pi }^{\pi }f(x)\sin(nx)\,\mathrm {d} x,\quad n\geq 1\!\,$

se imenujejo Fourierovi koeficienti za funkcijo $f(x)\!\,$.

Včasih se uporablja tudi Fourierove vrste za $f\!\,$, ki se jih označuje z:

$(S_{N}f)(x)={\frac {a_{0}}{2}}+\sum _{n=1}^{N}\,[a_{n}\cos(nx)+b_{n}\sin(nx)],\quad N\geq 0\!\,.$

Delne vsote za $f\!\,$ so trigonometrični polinomi. Pričakuje se, da funkcije $S_{N}\!\,$ za $f\!\,$ dajejo približek, ki se približuje vrednosti za $f\!\,$, ko gre $N\!\,$ proti neskončnosti. Neskončna vsota v obliki:

${\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\,[a_{n}\cos(nx)+b_{n}\sin(nx)]\!\,$

se imenuje Fourierova vrsta za $f\!\,$.

Fourierova vrsta ne konvergira vedno, saj se včasih celo za neko vrednost $x_{0}\!\,$ vsota vrste v tej točki razlikuje od vrednosti $f(x_{0})\!\,$ te funkcije. Harmonična analiza je področje, ki se ukvarja s konvergenco Fourierovih vrst. Kadar je kvadrat funkcije integrabilen na intervalu $[-\pi ,\pi ]\!\,$, takrat Fourierova vrsta konvergira skoraj v vsaki točki. Predpostavi se lahko, da Fourierova vrsta konvergira v vsaki točki razen v točkah nezveznosti.

Zgled periodične funkcije, ki se imenuje žagasti val.

Animacija prvih petih zaporednih delnih Fourierovih vrst.

Zgled

V zgledu se obravnava žagasti val in se ga razvije v Fourierovo vrsto. Žagasti val se opiše z naslednjo funkcijo:

$f(x)=x,\quad \mathrm {za} -\pi <x<\pi \!\,,$

$f(x+2\pi )=f(x),\quad \mathrm {za} -\infty <x<\infty \!\,.$

V tem primeru se dobi za Fourierove koeficiente:

${\begin{aligned}a_{0}&{}={\frac {1}{\pi }}\int _{-\pi }^{\pi }x\,\mathrm {d} x=0.\\a_{n}&{}={\frac {1}{\pi }}\int _{-\pi }^{\pi }x\cos(nx)\,\mathrm {d} x=0,\quad n\geq 0.\\b_{n}&{}={\frac {1}{\pi }}\int _{-\pi }^{\pi }x\sin(nx)\,\mathrm {d} x=-{\frac {2}{n}}\cos(n\pi )+{\frac {2}{\pi n^{2}}}\sin(n\pi )=2\,{\frac {(-1)^{n+1}}{n}},\quad n\geq 1.\end{aligned}}$

Lahko se dokaže, da Fourierova vrsta konvergira k vrednosti $f(x)\!\,$ v vsaki točki, kjer je funkcija $f\!\,$ diferenciabilna. Torej se lahko zapiše:

${\begin{aligned}f(x)&={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\left[a_{n}\cos \left(nx\right)+b_{n}\sin \left(nx\right)\right]\\&=2\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}\sin(nx),\quad \mathrm {za} \quad x-\pi \notin 2\pi Z.\end{aligned}}$

Eksponentna Fourierova vrsta

Uporabi se Eulerjev obrazec, ki ima obliko:

$e^{inx}=\cos(nx)+i\sin(nx)\!\,,$

kjer je:

• $i\!\,$ – imaginarna enota

S tem se dobi bolj zgoščeno obliko za Fourierovo vrsto:

$f(x)=\sum _{n=-\infty }^{\infty }c_{n}e^{inx}\!\,.$

Fourierovi koeficienti pa so:

$c_{n}={\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(x)e^{-inx}\,\mathrm {d} x\!\,.$

$a_{n}={c_{n}+c_{-n}}\quad {\text{ za }}n=0,1,2,\dots \!\,$

$b_{n}=i(c_{n}-c_{-n})\quad {\text{ za }}n=1,2,\dots \!\,$

in:

$c_{n}={\begin{cases}{\frac {1}{2}}(a_{n}-ib_{n})&n>0\\\quad {\frac {1}{2}}a_{0}&n=0\\{\frac {1}{2}}(a_{-n}+ib_{-n})&n<0\\\end{cases}}$

Zelo primerno je uporabiti obliko za $f\!\,$ tako, da se dobi obrazec v obliki:

$f(x)=\sum _{n=-\infty }^{\infty }{\hat {f}}(n)\cdot e^{inx}\!\,.$

V tehniki se pogosto uporablja naslednjo obliko:

$f(x)=\sum _{n=-\infty }^{\infty }F[n]\cdot e^{inx}\!\,,$

kjer:

• $F[n]\!\,$ pomeni, da je uporabljena nezvezna domena frekvenc. Zelo pogosto v tehniki spremenljivka $x\!\,$ predstavlja čas.

Fourierove vrste v splošnem intervalu

Obravnava se splošni interval $[a,a+\tau ]\!\,$, kjer je s periodo $\tau \!\,$ za vsa realna števila definirana funkcija $g(x)\!\,$ s kompleksnimi koeficienti $G(n)\!\,$. Lahko se zapiše:

$g(x)=\sum _{n=-\infty }^{\infty }G[n]\cdot e^{i2\pi {\frac {n}{\tau }}x}\!\,.$

Če je funkcija kvadratno integrabilna (velja: $\int _{-\infty }^{\infty }|f(x)|^{2}\,\mathrm {d} x<\infty \!\,$), v intervalu $[a,a+\tau ]\!\,$, se jo lahko v tem intervalu prikaže z zgornjim obrazcem. To pa pomeni, da takrat, ko se dobi koeficiente za funkcijo $h(x)\!\,$ z:

$G[n]={\frac {1}{\tau }}\int _{a}^{a+\tau }h(x)\cdot e^{-i2\pi {\frac {n}{\tau }}x}\,\mathrm {d} x\!\,,$

potem je $g(x)\!\,$ povsod na intervalu $[a,a+\tau ]\!\,$ enak $h(x)\!\,$. Iz tega sledi, da ima $h(x)\!\,$ periodo enako $\tau \!\,$ in, da naslednje

• sta $g(x)\!\,$ in $h(x)\!\,$ povsod enaka, razen na mestih nezveznosti
• $a\!\,$ se lahko poljubno izbere. Najpogosteje se izbere $a=0\!\,$ in $a=\tau /2\!\,$.

Fourierove vrste v kvadratu

Definira se lahko tudi Fourierove vrste za dve spremenljivki x in y v kvadratu $[-\pi ,\pi ]\times [-\pi ,\pi ]\!\,$:

$f(x,y)=\sum _{j,k\in \mathbb {Z} }c_{j,k}e^{ijx}e^{iky}\!\,,$

kjer je:

$c_{j,k}={1 \over 4\pi ^{2}}\int _{-\pi }^{\pi }\int _{-\pi }^{\pi }f(x,y)e^{-ijx}e^{-iky}\,\mathrm {d} x\,\mathrm {d} y\!\,.$

Hilbertov prostor

Če se obravnava Hilbertove prostore, množica funkcij $\{e_{n}=e^{inx},n\in \mathbb {Z} \}\!\,$ tvori ortonormalno bazo prostora $L^{2}([-\pi ,\pi ])\!\,$ za kvadratno integrabilne funkcije v $[-\pi ,\pi ]\!\,$. Ta prostor je Hilbertov prostor z notranjim produktom za poljubna dva elementa $f\!\,$ in $g\!\,$, ki je definiran kot:

$\langle f,\,g\rangle \;{\stackrel {\mathrm {def} }{=}}\;{\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(x){\overline {g(x)}}\,\mathrm {d} x\!\,.$

Osnovne Fourierove vrste v Hilbertovih prostorih se lahko zapiše kot:

$f=\sum _{n=-\infty }^{\infty }\langle f,e_{n}\rangle \,e_{n}\!\,.$

To pa je enakovredno s kompleksno eksponentno obliko (glej zgoraj). Oblika s sinusom in kosinusom tvori ortogonalno množico:

$\int _{-\pi }^{\pi }\cos(mx)\,\cos(nx)\,\mathrm {d} x=\pi \delta _{mn},\quad m,n\geq 1,\!\,$

$\int _{-\pi }^{\pi }\sin(mx)\,\sin(nx)\,\mathrm {d} x=\pi \delta _{mn},\quad m,n\geq 1\!\,$

$\int _{-\pi }^{\pi }\cos(mx)\,\sin(nx)\,\mathrm {d} x=0\,\!\,,$

kjer je:

• $\delta _{mn}\!\,$ – Kroneckerjeva delta.

Značilnosti

Funkcija $f\!\,$ pripada $C^{k}(\mathbb {T} )\!\,$, če je $f\!\,$ funkcija s periodo $2\pi \!\,$ nad $\mathbb {R} \!\,$ in, če je ta k-krat odvedljiva in je k-ti odvod zvezen. Označi se n-ti Fourierov koeficient z ${\widehat {f}}(n)\!\,$.

• če je $f\!\,$ periodična liha funkcija, potem so $a_{n}=0\!\,$ za vse $n\!\,$
• če je $f\!\,$ periodična soda funkcija, potem so $b_{n}=0\!\,$ za vse $n\!\,$
• če je $f\!\,$ integrabilna funkcija velja $\lim _{|n|\rightarrow \infty }{\hat {f}}(n)=0\!\,$ ter $\lim _{n\rightarrow +\infty }a_{n}=0\!\,$ in $\lim _{n\rightarrow +\infty }b_{n}=0\!\,$. To je Riemann-Lebesguov izrek
• dvojno neskončno zaporedje $\{a_{n}\}\!\,$ v $c_{o}\!\,$ je zaporedje Fourierovih koeficientov funkcije v $L^{1}[0,2\pi ]\!\,$, če in samo če je to konvolucija v $\ell ^{2}(\mathbb {Z} )\!\,$
• Parsevalov izrek: če je $f\in L^{2}([-\pi ,\pi ])\!\,$, potem je tudi $\sum _{n=-\infty }^{\infty }|{\hat {f}}(n)|^{2}={\frac {1}{2\pi }}\int _{-\pi }^{\pi }|f(x)|^{2}\,\mathrm {d} x\!\,$
• Plancherelov izrek: če so $c_{0},\,c_{\pm 1},\,c_{\pm 2},\ldots \!\,$ koeficienti in velja $\sum _{n=-\infty }^{\infty }|c_{n}|^{2}<\infty \!\,$, potem obstaja funkcija $f\in L^{2}([-\pi ,\pi ])\!\,$ tako, da velja ${\hat {f}}(n)=c_{n}\!\,$ za vsak $n\!\,$
• prvi konvolucijski izrek pravi, da takrat, ko sta $f\!\,$ in $g\!\,$ v L¹([−π, π]), potem velja tudi ${\widehat {f*g}}(n)=2\pi {\hat {f}}(n){\hat {g}}(n)\!\,$, kjer je ƒ ∗ g konvolucija s periodo $2\pi \!\,$ funkcij $f\!\,$ in $g\!\,$
• drugi konvolucijski izrek pravi, da je ${\widehat {f\cdot g}}={\hat {f}}*{\hat {g}}\!\,$.

Posplošitve

Obstaja več vrst posplošitev Fourierovih vrst. Njihovo proučevanje se imenuje harmonična analiza.

Približki in konvergenca Fourierovih vrst

Glej tudi: Gibbsov pojav

Gibbsov pojav

Približek reda 10 za pravokotni val.

Približek reda 50 za pravokotni val.

Približek reda 250 za pravokotni val.

Zelo pomembno vprašanje je povezano s konvergenco Fourierovih vrst. Pogosto je treba zamenjati neskončno vrsto $\sum _{-\infty }^{\infty }\!\,$ s končno: $(S_{N}f)(x)=\sum _{n=-N}^{N}{\hat {f}}(n)e^{inx}\!\,$. Takšna vrsta se imenuje delna vsota. Želi se vedeti kako vrednost $(S_{N}f)(x)\!\,$ konvergira k $f(x)\!\,$, ko gre $N\!\,$ proti neskončnosti.

Divergenca Fourierovih vrst

Fourierove vrste so izredno dobro konvergentne. Vrste, ki bi bile divergentne so zelo redke. V letu 1922 je ruski matematik Andrej Nikolajevič Kolmogorov (1903–1987) v enem svojih del podal primer integrabilne funkcije, katere Fourierova vrsta je skoraj povsod divergentna.

Glej tudi

• Laurentova vrsta
• harmonična analiza
• spektralna teorija
• Fourierova transformacija
• Fejérov izrek
• Dichletovo jedro

Zunanje povezave

• Fourierova vrsta Arhivirano 2013-08-01 na Wayback Machine. (slovensko)
• Fourierova vrsta na e-študij Arhivirano 2012-03-18 na Wayback Machine. (slovensko)
• Weisstein, Eric W. "Fourier Series". MathWorld.
• Apleti za prikaz Fourierovih vrst (angleško)
• Fourierove vrste (angleško)
• Učbenik (angleško)
• Maths Online (angleško)
• Fourierove vrste in Fourierovi integrali (angleško)