Harmonična vrsta

Harmónična vŕsta je v matematiki divergentna vrsta:

$\sum_{n=1}^{\infty} \frac{1}{n} = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \cdots \!\, .$

Tako se imenuje, ker so valovne dolžine delnih tonov nihajoče strune sorazmerne z 1, 1/2, 1/3, 1/4, ... . Vsak člen vrste za prvim je harmonična sredina sosednjih dveh členov, predhodnega in naslednjega, $H(a_{n-1}, a_{n+1})$. Na primer:

$\frac{1}{2} = \frac{2}{1+\frac{1}{\frac{1}{3}}} , \quad \frac{1}{3} = \frac{2}{\frac{1}{\frac{1}{2}}+\frac{1}{\frac{1}{4}}} , \quad \frac{1}{4} = \frac{2}{\frac{1}{\frac{1}{3}}+\frac{1}{\frac{1}{5}}} , \quad \frac{1}{5} = \frac{2}{\frac{1}{\frac{1}{4}}+\frac{1}{\frac{1}{6}}} , \quad \cdots , \quad \frac{1}{a_{n}} = \frac{2}{\frac{1}{\frac{1}{a_{n-1}}}+\frac{1}{\frac{1}{a_{n+1}}}} \!\, .$

Zaporedje členov s takšnimi značilnostmi je harmonično zaporedje, harmonična vrsta pa je vsota harmoničnega zaporedja (vsota členov harmoničnega zaporedja).

Tudi izraz harmonična sredina izvira iz glasbe.

Vrsta divergira, sicer počasi, k neskončnosti (vsota prvih 10⁴³ členov je manj kot 100). To se lahko lepo pokaže z dejstvom, da je harmonična vrsta po členih večja ali enaka z vrsto:

$\begin{align} \sum_{n=1}^{\infty} \frac{1}{n} & {} = 1 + \left[\frac{1}{2}\right] + \left[\frac{1}{3} + \frac{1}{4}\right] + \left[\frac{1}{5} + \frac{1}{6} + \frac{1}{7} + \frac{1}{8}\right] + \left[\frac{1}{9}+\cdots\right] + \cdots \\ \sum_{n=1}^{\infty} \frac{1}{2^{\lceil \log_2 n \rceil}} \! & {} = 1 + \left[\frac{1}{2}\right] + \left[\frac{1}{4} + \frac{1}{4}\right] + \left[\frac{1}{8} + \frac{1}{8} + \frac{1}{8} + \frac{1}{8}\right] + \left[\frac{1}{16} + \cdots\right] + \cdots \\ & {} = 1 + \ \frac{1}{2}\ \ \ + \quad \frac{1}{2} \ \quad + \ \qquad\quad\frac{1}{2}\qquad\ \quad \ + \quad \ \ \frac{1}{2} \ \quad + \ \cdots \!\, , \end{align}$

ki očitno divergira. Ta dokaz je podal Nicole Oresme v 14. stoletju in predstavlja enega od viškov srednjeveške matematike. Kasneje so dokaze podali Pietro Mengoli, Johann in Jakob Bernoulli v 17. stoletju. Celo vsota obratnih vrednosti praštevil divergira k neskončnosti, čeprav je to težje dokazati.

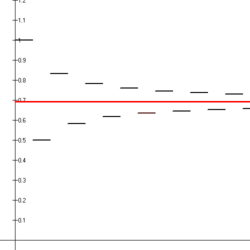
Konvergenca alternirajoče harmonične vrste

Prvih štirinajst delnih vsot alternirajoče harmonične vrste (črni odseki) kaže njeno konvergenco k naravnemu logaritmu od 2 (rdeča premica)

Alternirajoča harmonična vrsta na drugi strani konvergira - je pogojno konvergentna:

$\sum_{n = 1}^{\infty} \frac{(-1)^{n + 1}}{n} = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \cdots = \ln 2 = 0,693\,147\,180\,\dots \!\, .$

Konvergenco alternirajoče harmonične vrste je leta 1650 v članku dokazal Mengoli. Ta enakost je posledica Mercatorjeve vrste, Taylorjeve vrste za naravni logaritem. Po obliki Mercatorjevi vrsti sorodna je vrsta:

$\sum_{n=0}^{\infty} \frac{(-1)^{n}}{2n+1} = 1 - \frac{1}{3} + \frac{1}{5} -\frac{1}{7} +\cdots = \arctan (1 )=\frac{\pi}{4} \!\, .$

To je posledica razvoja krožne fukncije arkus tangens v Taylorjevo vrsto, katere konvergenčni polmer je enak 1.

Delne vsote

n-ta delna vsota harmonične vrste:

$H_{n} = \sum_{k = 1}^{n} \frac{1}{k} \!\,$

se imenuje n-to harmonično število.

Razlika med n-tim harmoničnim številom in naravnim logaritmom od n konvergira k Euler-Macheronijevi konstanti:

$\lim_{n \to \infty} \left(H_{n} - \ln n \right) = \gamma \!\, .$

Razlika med dvema različnima harmoničnima številoma ni nikoli celo število.

Splošna harmonična vrsta

Splošna harmonična vrsta ima obliko:

$\sum_{n=0}^{\infty}\frac{1}{an+b} \!\, ,$

kjer sta konstanti a in b končni realni števili.

Vse splošne harmonične vrste divergirajo.

Glej tudi

• alikvotni toni