Praštevilski izrek

Iz Wikipedije, proste enciklopedije

Práštevílski izrèk (tudi izrèk o gostôti práštevíl) je v matematiki izrek o asimptotični porazdelitvi praštevil.

Praštevilski izrek v grobem pravi, da če naključno izberemo poljubno število blizu nekega velikega števila n, je verjetnost da bo to število praštevilo enaka približno 1 / ln n, kjer ln n označuje naravni logaritem. Na primer za n = 10.000 je približno eno od devetih števil praštevilo, za n = 1.000.000.000 pa je le eno praštevilo med 21-timi izbranimi števili.

Razvidno je, da so praštevila porazdeljena naključno, vendar na žalost ne vemo kaj 'naključno' pomeni.

-- R.C. Vaughan (februar 1990).

Vsebina

1 Vsebina izreka
2 Eulerjeva obravnava
3 Dirichletova posplošitev
4 Pregled zgodnje zgodovine izreka
5 Razpredelnica funkcij π(ξ), ξ / ln ξ in Li(ξ)
6 Riemannova razširitev in dokaz
7 Groba skica dokaza
8 Teorija Dirichletovih vrst
9 Elementarni dokazi
10 Praštevilski izrek za aritmetična zaporedja
11 Domene funkcije števila praštevil
12 Približki za n-to praštevilo
13 Podobnost za nerazcepne polinome v končnem obsegu
14 Glej tudi
15 Opombe
16 Viri
17 Zunanje povezave

[uredi] Vsebina izreka

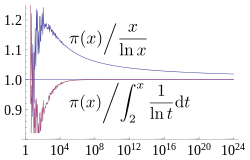
π(ξ) je aritmetična funkcija število praštevil, ki podaja število praštevil manjših ali enakih ξ za poljubno realno število ξ. π(10) = 4, saj so štiri praštevila (2, 3, 5 in 7) manjša ali enaka 10. Praštevilski izrek pravi, da je limita kvocienta funkcij π(ξ) in ξ / ln ξ enaka 1, ko se ξ približuje neskončnosti:

$\lim_{\xi\to +\infty}\frac{\pi(\xi)}{\xi/\ln\,\xi}=1 \; .$

Izrek sam ne pove nič o limiti razlik dveh funkcij, ko ξ narašča v neskončnost. Obnašanje te razlike je zapleteno in je povezano z Riemannovo domnevo. Izrek izjavlja, da je ξ / ln ξ približno enako π(ξ) v smislu, da se relativna napaka tega približka približuje 0, ko ξ naraste prek vseh meja.

Praštevilski izrek je enakovreden izjavi, da je n-to praštevilo p_n približno enako n ln n), kjer se spet relativna napaka približuje 0, ko n narašča v neskončnost.

[uredi] Eulerjeva obravnava

Leta 1737 je Euler vpeljal klasično Euler-Riemannovo funkcijo ζ, določeno za vsa realna števila s večja od 1:

$\zeta(s) = \sum_{k=1}^{\infty} {1\over k^{s}} = {1\over 1^{s}} + {1\over 2^{s}} + {1\over 3^{s}} + {1\over 4^{s}} + {1\over 5^{s}} + ... \; ,$

kjer so k pozitivna cela števila. Za števila $s \le 1$ (ali bolje za realni del) je gornja vsota neskončna, tako da $ζ(s)$ za taka števila ni določena. Za vsako število s>1 ima gornja vsota določeno končno vrednost. Pokazal je, da je za vsak tak s vrednost funkcije $ζ(s)$ enaka neskončnemu Eulerjevemu produktu:

$\zeta(s) = {\prod_{p=2 \atop p \in P}^{\infty}} { 1\over 1-{1\over p^{s}}} = { 1\over 1-{1\over 2^{s}}} \cdot { 1\over 1-{1\over 3^{s}}} \cdot { 1\over 1-{1\over 5^{s}}} \cdot { 1\over 1-{1\over 7^{s}}} \cdot { 1\over 1-{1\over 11^{s}}} \cdot { 1\over 1-{1\over 12^{s}}} \cdot ... \; .$

Prednost produkta je v tem, da ne vsebuje ničel v polravnini. Njegov rezultat je presenetljiv, saj povezuje funkcijo $ζ(s)$ z neskončno množico praštevil P, osnovnih gradnikov števil. Praštevila so prisotna v analizi, ki je odraz neskončne narave matematike. Infinitezimalni račun, Newtonovi polinomi, funkcija Γ in funkcija $ζ$ funkcija vse sodijo v analizo. Funkcionalno enakost funkcije $ζ(s)$ je Euler odkril leta 1761. Funkcija:

${1\over \sqrt \pi^2} \Gamma({s\over 2}) \zeta (s) \;$

ostaja nespremenjena, kadar s zamenjamo z 1 - s. Pomena enakosti ne moremo videti neposredno, ker so funkcije določene v samostojnih polravninah ločenih s kritičnim trakom. Trak vsebuje kompleksna števila katerih realni deli ležijo natančno med 0 in 1. To pomeni da imata tako dve funkciji naravni nadaljevanji preko mej traku in ti dve sta enaki. Za funkcijo $ζ(s)$ velja funkcionalna enačba:

$\zeta(s) = 2^{s} \pi^{s-1} \sin \left({\pi s\over 2}\right) \Gamma (s-1) \zeta(1-s) \; ,$

za vse s iz $\mathbb{C}$ - {0,1}. S to enačbo si pomagamo pri analitičnem nadaljevanju. Pri s = 1 ima funkcija $ζ(s)$ enostavni pol z ostankom 1. Euler je lahko izračunal $ζ(2 k)$ za vsako sodo celo število 2k z enačbo:

$\zeta(2k) = { B_{2k}(2\pi)^{2k}\over 2(2k)!} \; ,$

kjer so $B 2 k$ Bernoullijeva števila. Od tu vidimo, da je $ζ(2) = π 2 / 6$ , $ζ(4) = π 4 / 90$ , $ζ(6) = π 6 / 945$ , $ζ(8) = π 8 / 9450$ , $ζ(10) = π 10 / 93555$ in tako naprej. Te vrednosti nam dajo znane neskončne vrste za π. Euler je podal vrednosti za $ζ(2)$ do $ζ(26)$ za sode n. Stieltjes je leta 1887 podal na 30 števk natančno vrednosti za $ζ(2)$ do $ζ(70)$ . Števci $ζ(2 n)$ za n=1,2,3,... tvorijo zaporedje {6, 90, 945, 9450, 93555, 638512875, ...}. Primeri za liha cela števila pa niso tako enostavni. Ramanujan je z velikim uspehom raziskoval tudi takšne primere. Za n > 1 in $n \equiv 3 ({\rm mod} \; 4)$ velja na primer:

${\zeta(n)} = {2^{n-1}\pi^{n}\over (n+1)!} \sum_{k=0}^{(n+1)/2} (-1)^{k-1} {n+1\choose 2k} B_{n+1-2k}B_{2k} - 2 \sum_{k=1}^{\infty} {1\over k^{n}(e^{2\pi k}-1)} \; ,$

kjer je ${n\choose k}$ binomski koeficient. Našli so še druge enačbe za nekatere lihe n.

Sorodni izrek za harmonično vrsto recipročnih vrednosti naravnih števil:

$H(n) = \sum_{k=1}^{\infty} {1\over k} = {1\over 1} + {1\over 2} + {1\over 3} + {1\over 4} + {1\over 5} + {1\over 6} + {1\over 7} + ... \;$

nam pove, da vrsta nima končne vsote in podobno divergira kot $ln n$ . Euler je poznal ta izrek in je pokazal, da velja:

$H(n) \sim \ln n$

in

$H(n) - \ln n \sim \gamma \; ,$

kjer je $γ$ ≈ 0,57721 56649 Euler-Mascheronijeva konstanta. Euler se je spraševal za praštevilsko harmonično vrsto, ki jo dobimo če seštejemo recipročne vrednosti vseh praštevil:

$P(p) = \sum_{p=1 \atop p \in P}^{\infty} {1\over p} = {1\over 1} + {1\over 2} + {1\over 3} + {1\over 5} + {1\over 7} + {1\over 11} + {1\over 13} + ... \;$

Ali ima sedaj $P (p)$ končno ali neskončno vsoto? Naravni način odgovora na vprašanje je delitev harmonične vrste na dva dela: tistega, ki vsebuje vsa praštevila in preostanek harmonične vrste:

$\left[{1\over 1} + {1\over 2} + {1\over 3} + {1\over 5} + {1\over 7} + {1\over 11} + {1\over 13} + ... \right] + \left[{1\over 4} + {1\over 6} + {1\over 8} + {1\over 9} + {1\over 10} + {1\over 12} + {1\over 14} + ...\right] \;$

Potem poskušamo pokazati, da ima drug del končno vsoto. To bi pomenilo, da prvi del povzroča, da ima harmonična vrsta $H (n)$ neskončno vsoto. Prvi del je praštevilska harmonična vrsta in bi tako imela neskončno vsoto. To je dobra zamisel, vendar naletimo na nepričakovano težavo. Ker harmonična vrsta divergira, je ne moremo na ta način deliti. Euler se je lotil težave drugače. Vzemimo neko celo realno število s malo večje od 1 in namesto, da opazujemo harmonično vrsto $H (n)$ , opazujmo raje sorodno vrsto $ζ(s)$ . Ker smo vzeli s večji od 1, ima ta vrsta končno vsoto in jo zato lahko delimo na dva končna dela: tistega, ki vsebuje vsa praštevila in tistega, ki vsebuje vsa sestavljena števila:

$\zeta(s) = \left[ {1\over 1^{s}} + {1\over 2^{s}} + {1\over 3^{s}} + {1\over 5^{s}} + {1\over 7^{s}} + {1\over 11^{s}} + {1\over 13^{s}} + ...\right] + \left[{1\over 4^{s}} + {1\over 6^{s}} + {1\over 8^{s}} + {1\over 9^{s}} + {1\over 10^{s}} + {1\over 12^{s}} + {1\over 14^{s}} + ... \right] \; .$

Potem poskušamo pokazati, da če približujemo s vedno bližje 1, bo prva vsota:

${1\over 1^{s}} + {1\over 2^{s}} + {1\over 3^{s}} + {1\over 5^{s}} + {1\over 7^{s}} + {1\over 11^{s}} + {1\over 13^{s}} + ...$

naraščala preko vsake meje in pri s = 1 bo praštevilska harmonična vrsta:

$P(p) = \sum_{p=1 \atop p \in P}^{\infty} {1\over p} = {1\over 1} + {1\over 2} + {1\over 3} + {1\over 5} + {1\over 7} + {1\over 11} + {1\over 13} + ... \;$

imela neskončno vsoto. Pri preučevanju $ζ(s)$ je Euler zasledoval podobno enačbo vsote geometrične vrste:

${1\over 1-x} = 1 + x + x^{2} + x^{3} + x^{4} + x^{5} + ... \quad (0<x<1) \; .$

Za vsako praštevilo p in vsak s > 1 lahko zapišemo $x = 1 / p s$ kot:

${ 1\over 1-\left({1\over p}\right)^{s} } = { 1\over p^{1} } + { 1\over p^{s} } + { 1\over p^{2s} } + { 1\over p^{3s} } + { 1\over p^{4s} } + { 1\over p^{5s} } + ... \; .$

Izraz na levi strani je seveda izrazit člen v Eulerjevemu neskončnemu produktu in nam zgornja enačba zagotavlja neskončno vsoto za vsak člen v neskončnem produktu. Euler je naprej pomnožil vse te neskončne vsote, da bi dobil drugačno obliko svojega neskončnega produkta. Z uporabo običajnih algebrskih pravil za množenje (končnega števila končnih) vsot na neskočno mnogo neskončnih vsot lahko vidimo, če izpišemo desno stran kot eno neskončno vsoto, bodo njeni izrazi oblike:

$1\over p_1^{k_1 s} ... p_n^{k_n s} \; ,$

kjer so $p 1,..., p n$ različna praštevila in $k 1,..., k n$ pozitivna cela števila in vsaka njihova kombinacija nastopi natanko enkrat. Po osnovnem izreku algebre lahko vsako pozitivno celo število izrazimo v obliki $p_1^{k_1 s} ... p_n^{k_n s}$ . Zaradi tega je desna stran preureditev vsote:

${1\over 1^{s}} + {1\over 2^{s}} + {1\over 3^{s}} + {1\over 4^{s}} + {1\over 5^{s}} + {1\over 6^{s}} + ... \; ,$

oziroma $ζ(s)$ . Eulerjeva enačba neskončnega produkta za $ζ(s)$ označuje začetek analitične teorije števil.

[uredi] Dirichletova posplošitev

Leta 1837 je Dirichlet posplošil Eulerjevo metodo za dokaz ali v vsakem aritmetičnem zaporedju $a, a + k, a + 2 k, a + 3 k,...$ , kjer a in k nimata skupnega faktorja (sta si tuja, oziroma relativno praštevili), obstaja neskončno število praštevil. Na Evklidov izrek lahko gledamo kot na poseben primer tega za aritmetično zaporedje 1,3,5,7, ... vseh lihih celih števil. Dirichlet je za to priložnost posplošil Euler-Riemannovo funkcijo $ζ$ tako, da so vsa praštevila ločena v posamične razrede glede na to, kakšen ostanek imajo pri deljenju s k. Njegova modificirana funkcija ζ ima obliko:

$L(s,\chi) = \sum_{k=1}^\infty {\chi(k) \over {k^{s}} } = {\chi(1) \over {1^{s}} } + {\chi(2) \over {2^{s}} } + {\chi(3) \over {3^{s}} } + {\chi(4) \over {4^{s}} } + {\chi(5) \over {5^{s}} } + ... \; ,$

kjer je $χ(n)$ posebna oblika funkcije, ki jo je Dirichlet imenoval »karakter«, in ta deli praštevila na zahtevan način. Posebej velja $χ(m n) = χ(m)χ(n)$ za vsak $m, n$ . Druga pogoja sta še, da je $χ(n)$ odvisna le od ostanka pri deljenju n s k in $χ(n) = 0$ , če imata n in k skupni faktor. Vsaka funkcija oblike $L (s,χ)$ , kjer je realno število s > 1 in $χ$ karakter, je znana kot Dirichletova L-vrsta. Euler-Riemannova funkcija $ζ$ je poseben primer, ki nastane, če vzamemo $χ(n) = 1$ za vse n. Matematiki so posplošili spremenljivko s in števila $χ(n)$ v kompleksno področje in s posplošeno obliko dokazali veliko lastnosti praštevil in tako pokazali, da so L-vrste zelo močno orodje pri študiju praštevil. Ključni rezultat o L-funkcijah je ta, da jih lahko skupaj z $ζ(s)$ izrazimo kot neskončni produkt preko praštevil (Eulerjev produkt):

$L(x,\chi) = {\prod_{p=2 \atop p \in P}^{\infty}} { 1\over 1-{\chi(p)\over p^{s}} } = { 1\over 1-{\chi(2)\over 2^{s}} } \cdot { 1\over 1-{\chi(3)\over 3^{s}} } \cdot { 1\over 1-{\chi(5)\over 5^{s}} } \cdot { 1\over 1-{\chi(7)\over 7^{s}} } \cdot { 1\over 1-{\chi(11)\over 11^{s}} } \cdot ... \; ,$

kjer je realni del s pozitiven.

Med prvimi desetimi števili je kar polovica praštevil, med prvimi 1000 pa le približno 1/6. Zdi se, da ni kakšnega splošnega pravila, po katerem bi bila praštevila razporejena med naravnimi števili. Med 9 999 900 in 10 000 000 je na primer 9 praštevil. Med 10 000 000 in 10 000 100 pa le 2, in sicer 10 000 019 in 10 000 079. Obstajajo celo poljubno dolgi odseki zaporednih naravnih števil, med katerimi ni nobenega praštevila. Za poljuben n med številoma $n! + 2$ in $n! + n$ ni nobenega praštevila. Matematiki menijo, da so praštevilski dvojčki razporejeni povsem slučajno. Celo tega ne vemo, ali je praštevilskih dvojčkov končno mnogo ali jih je neskončno.

[uredi] Pregled zgodnje zgodovine izreka

Praštevilski izrek govori o asimptotičnem obnašanju aritmetične funkcije $π(ξ)$ , števila praštevil manjših ali enakih realnemu številu $ξ$ . Legendre je leta 1796 domneval in leta 1798 v knjigi Esai sur la Theorie des Nombres objavil ugotovitev za velike $ξ$ :

$\pi(\xi) \sim {n\over {A \ln n - B}} \; ,$

z A = 1 in B = 1,08366, ki se včasih imenuje Legendrova konstanta. Pomagal si je z Eratostenovim sitom in je do tega rezultata prišel povsem empirično na podlagi preučevanja Felklovih in Vegovih razpredelnic praštevil, manjših od 400.000. Zato število B ni kaj posebnega. Legendre ga je enostavno izbral tako, da je dobil kar najboljši približek. Medtem ko je Legendre pripravljal svojo knjigo, je funkcijo $π(ξ)$ preučeval tudi štirinajstletni Gauss. Leta 1792 je kot 15-leten zapisal (objavil pa šele leta 1863):

$p \; \hbox{pod} \;\; \xi \, (= \infty) {\xi\over \hbox{l} \, \xi} \; .$

Če »praštevila pod $ξ$ « nadomestimo z enakovredno vrednostjo $π(ξ)$ , znak l $ξ$ z $lnξ$ in $(= \infty)$ z besedilom za velike $ξ$ , dobimo njegovo mladostno oceno:

$\pi(\xi) \sim {\xi\over \ln \xi} \quad \hbox{za velike} \;\; \xi \; ,$

z deljenjem s $ξ$ pa obliko praštevilskega izreka. Očitno je mladi Gauss že razumel to lastnost praštevil, zakaj pa je ni razvil, najverjetneje ne bomo nikoli izvedeli. Na Božič 1849 je v pismu Enckeju zapisal:

Kot deček sem preučeval problem koliko praštevil je do dane točke. Iz svojih preračunov sem ugotovil, da je gostota praštevil okoli x približno $1/\log \, x$ .

Pozneje je domneval, da velja praštevilski izrek:

$\pi(\xi) \sim {\rm Li}(\xi) = \int_2^{\xi} {dt\over \ln t} \; ,$

kjer je Li $(ξ)$ neelementarna funkcija logaritemski integral ali integralski logaritem li $(x)$ brez Cauchyjeve glavne vrednosti (CGV). Logaritemski integral v kompleksnem je določen z:

${\rm li}(z) \equiv \int_{0}^z {dt\over \ln t} \quad \hbox{(za}\quad z>1 \; ,)$

Logaritemski integral v praštevilskem izreku je določen tako, da velja Li $(2) = 0$ :

${\rm Li}(\xi) \equiv \int_2^{\xi} {dt\over \ln t} = {\rm li}(\xi) - {\rm li}(2) \approx {\rm li}(\xi) - 1,045163780 = {\rm ei} (\ln \xi) \; ,$

kjer je ei $(ξ)$ eksponentni integral. Logaritemski integral močno namiguje na predstavo o tem da je 'gostota' praštevil okoli t enaka 1/lnt. Ta funkcija je povezana z logaritmom s Poincaréjevim, oziroma asimptotičnim razvojem:

$\mbox{Li}(\xi) = \frac{\xi}{\ln \xi} \sum_{k=0}^\infty \frac{k!}{(\ln \xi)^k} = \frac{\xi}{\ln \xi} + \frac{\xi}{(\ln \xi)^2} + \frac{2\xi}{(\ln \xi)^3} + \cdots$

Da se ognemo singularni vrednosti v točki 1, včasih vzamemo konstanto, označeno s c ali $μ > 1$ tako, da velja:

$CGV \int_0^\mu {1\over \ln t} dt = 0 \; .$

Tako lahko pri $ξ > 1$ zamenjamo CGV $\int_0^{\xi} 1/\ln t dt$ z $\int_{\mu}^{\xi} 1/\ln t dt$ . Ta način je prvi uporabil Ramanujan in se sedaj $μ$ ≈ 1.4513692348... imenuje Ramanujan-Soldnerjeva konstanta ali Soldnerjeva konstanta in predstavlja ničlo enačbe li $(ξ) = 0$ . Ramanujan je dobil vrednost $μ$ ≈ 1,451363380... Ta konstanta se pojavlja v naslednji obliki praštevilskega izreka:

$\pi(\xi) = \sum_{n=1}^{\infty} {\mu(n)\over n} \int_{\mu}^{\xi} {dt\over \ln t} \; ,$

kjer je $μ(m)$ Möbiusova multiplikativna aritmetična funkcija.

Graf, ki kaže primerjavo med π(ξ), ξ / ln ξ in Li(ξ)

Funkcija Li $(ξ)$ ima glavni člen $n/\ln \,n$ in je boljši priblišek od njega samega. Tako Legendreova in Gaussova enačba nakazujeta podobno domnevno asimtotično enakost med π(ξ) in ξ / ln ξ. Sicer se izkaže da je Gaussov približek precej boljši, če upoštevamo razlike namesto količnikov.

Čebišov je v dveh člankih leta 1848 in 1850 poskušal dokazati porazdelitveni zakon za praštevila. Njegovo delo je pomembno zaradi uporabe funkcije zeta ζ(s), ki je naznanjalo Riemannov članek iz leta 1859. Čebišov je leta 1851 dokazal malo šibkejši rezultat, da če $π(ξ) / (ξ / lnξ)$ res teži k limiti ko $ξ$ pobegne v neskončnost, potem mora biti limita enaka 1. Ni pa mogel pokazati, da ta limita res obstaja. Čeprav Čebišov ni docela dokazal praštevilskega izreka, je z uporabo ocene za π(ξ) leta 1850 dokazal Bertrandovo domnevo.

[uredi] Razpredelnica funkcij π(ξ), ξ / ln ξ in Li(ξ)

Naslednja razpredelnica kaže kako se obnašajo tri funkcije (π(ξ), ξ/ln(ξ) in Li(ξ)). Zadnji stolpec, ξ/ π(ξ) je povprečna praštevilska vrzel za praštevila, manjša od ξ:

ξ	π(ξ) ^[1]	π(ξ) - ξ/ln(ξ)^[2]	π(ξ) / (ξ/ ln ξ)	Li(ξ) - π(ξ)^[3]	ξ/π(ξ)
10¹	4	-0,3	0,921	2,2	2,500
10²	25	3,3	1,151	5,1	4,000
10³	168	23	1,161	10	5,952
10⁴	1.229	143	1,132	17	8,137
10⁵	9.592	906	1,104	38	10,430
10⁶	78.498	6.116	1,084	130	12,740
10⁷	664.579	44.159	1,071	339	15,047
10⁸	5.761.455	332.774	1,061	754	17,357
10⁹	50.847.534	2.592.592	1,054	1.701	19,666
10¹⁰	455.052.511	20.758.029	1,048	3.104	21,975
10¹¹	4.118.054.813	169.923.159	1,043	11.588	24,283
10¹²	37.607.912.018	1.416.705.193	1,039	38.263	26,590
10¹³	346.065.536.839	11.992.858.452	1,034	108.971	28,896
10¹⁴	3.204.941.750.802	102.838.308.636	1,033	314.890	31,202
10¹⁵	29.844.570.422.669	891.604.962.452	1,031	1.052.619	33,507
10¹⁶	279.238.341.033.925	7.804.289.844.392	1,029	3.214.632	35,812
10¹⁷	2.623.557.157.654.233	68.883.734.693.281	1,027	7.956.589	38,116
10¹⁸	24.739.954.287.740.860	612.483.070.893.536	1,025	21.949.555	40,420
10¹⁹	234.057.667.276.344.607	5.481.624.169.369.960	1,024	99.877.775	42,725
10²⁰	2.220.819.602.560.918.840	49.347.193.044.659.701	1,023	222.744.644	45,028
10²¹	21.127.269.486.018.731.928	446.579.871.578.168.707	1,022	597.394.254	47,332
10²²	201.467.286.689.315.906.290	4.060.704.006.019.620.994	1,021	1.932.355.208	49,636
10²³	1.925.320.391.606.818.006.727	37.083.513.766.592.669.113	1,020	7.236.148.412	51,939

Kot posledica praštevilskega izreka dobimo asimptotično oceno za n-to praštevilo p(n):

$p(n)\sim n\ln(n).$

Vidimo lahko tudi, da bo naključno izbrano število n praštevilo z verjetnostjo 1/ln(n).

[uredi] Riemannova razširitev in dokaz

Leta 1896 sta neodvisno drug od drugega de la Vallée Poussin in Hadamard dokazala praštevilski izrek, trditev, ki je bila razvidna že iz dotedanjih izračunov. Dokazala sta, da se z »naraščajočim n vrednost izraza $n / ln n$ bolj in bolj približuje funkciji $π(ξ)$ «. Pokazala sta da $ζ(s)$ nima nobenih ničel oblike $1 + i t$ , s tem, da za dokaz ni potrebno poznavanje drugih lastnosti $ζ(s)$ . Ta blesteči rezultat je enkrat za vselej in nedvoumno pokazal, da so praštevila razporejena po vzorcu, ki ga je možno opisati z matematičnimi sredstvi. Na njuno delo je močno vplival pomemben, čeprav komaj osem strani dolg Riemannov članek iz leta 1859 O številu praštevil, manjših od dane vrednosti (Über die Anzahl der Primzahlen unter einer gegebenen Grösse). To edino Riemannovo delo iz teorije števil je izredno pomembno, saj je z izvirnimi postopki preučevanja naravnih števil odkril mnoge nove zakonitosti. Te metode uporabljajo še danes. Ključni prijem, ki ga je Riemann vpeljal pri preučevanju porazdelitve praštevil, je razširitev funkcije $ζ(s)$ . Euler je določil funkcijo le za realna števila, ki so večja od 1. Riemann pa je Eulerjevo določitev razširil na vsa kompleksna števila $s = a + b i$ (z izjemo števila s = 1)^[4]. Pri tem moramo uporabiti analitično nadaljevanje funkcije. Razširjena funkcija $ζ(s)$ je določena kot krivuljni integral:

$\zeta(s) = {\Pi(-s)\over 2\pi i}\int_{C} {(-x)^{s}\over e^{x}-1} {dx\over x}\; ,$

pri čemer poteka krivulja C od $+\infty$ vzdolž realne osi, se tik pred izhodiščem ustavi, ga enkrat obkroži v nasprotni smeri urnega kazalca in se spet po realni osi vrne v $+\infty$ . Za vsak s > 0, pa je:

$\Pi(s) = \lim_{N \to \infty} {N!\over (s+1)(s+2)...(s+N)} {(N+1)^{s}}\; .$

Riemannova razširitev funkcije $ζ$ , imenovana tudi Riemannova funkcija ζ, je ključna za teorijo števil. Riemann je ugotovil, da je vrednost funkcije $ζ(s)$ za števila $S = - 2, - 4, - 6, - 8,...$ enaka 0. Pravimo, da so negativna soda cela števila ničle Riemannove funkcije $ζ$ . Nadalje je ugotovil, da obstaja še neskončno mnogo kompleksnih števil s, za katere je $ζ(s) = 0$ , in da je realni del vseh takih števil med 0 in 1. Vsa taka števila s so oblike $a + b i$ , pri čemer je $0 < a < 1$ . Riemannova domneva govori o netrivialnih kompleksnih ničlah Riemannove funkcije $ζ$ . Riemann je domneval, čeprav je poznal komaj kakšno kompleksno ničlo te funkcije, da je realni del vseh kompleksnih ničel funkcije $ζ(s)$ enak $1\over 2$ . Če je torej $ζ(s) = 0$ in s sodo pozitivno število, potem je po njegovi domnevi $s={1\over 2} + bi$ za kakšno realno število b.

Še boljša aproksimacija in ocena napake je dana z enačbo:

$\pi(\xi) = {\rm Li} (\xi) + O \left(\xi e^{-\frac{1}{15}\sqrt{\ln(\xi)}}\right)$

za $ξ$ → ∞, kjer je $O$ zapis Landauov simbol. Približek so še izboljšali z:

$\pi(\xi)={\rm Li} (\xi) + O \left(\xi \, \exp \left( -\frac{A(\ln \xi)^{3/5}}{(\ln \ln \xi)^{1/5}} \right) \right) \; .$

Izreka Hadamarda in de la Vallée-Poussin je kasneje v 20. stoletju postal znan kot praštevilski izrek. Zaradi povezave med Riemannovo funkcijo ζ(s) in π(ξ) ima RIemannova domneva pomembno vlogo v teoriji števil. Če bo rešena, bo moč najti mnogo natančnejšo napako v praštevilskem izreku kot je na voljo sedaj. Von Koch je leta 1901^[5] dokazal, da je Riemannova domneva enakovredna naslednji močnejši obliki praštevilskega izreka, ko $\xi\to\infty$ :

$\pi(\xi) = {\rm Li} (\xi) + O \left(\sqrt\xi \ln\xi\right) \; ,$

Če velja Riemannova domneva, je tukaj ocena napake še boljša kot zgoraj, kakšna pa je konstanta v $O$ zapisu, pa ne vemo. Ta povezava med številom praštevil in med ničlami kompleksne analitične funkcije je nabila ozračje matematike na začetku 20. stoletja. Kot je leta 1932 zapisal Ingham:

Rešitev [zgornje enačbe] ... bo verjetno neuspešna, ker prinaša zamisli, ki so zelo drugačne od izvirnega problema. Naravno se je vprašati po dokazu praštevilskega izreka, ki ni odvisen od funkcij kompleksne spremenljivke ... Kakor zgleda bo nemogoče najti pristen dokaz z 'realnimi spremenljivkami'.

Ingham je menil, da mora vsak dokaz vsebovati kompleksno analizo. Kako se je motil (kot tudi Hardy, Bohr in mnogi drugi). Leta 1949 sta Selberg in Erdös delno neodvisno pokazala elementarni dokaz praštevilskega izreka.

Konstanto v von Kochovi obliki je leta 1976 določil Schoenfeld^[6] in upošteval Riemannovo domnevo:

$|\pi(\xi)-{\rm li}(\xi)|<\frac{\sqrt \xi\,\ln \xi}{8\pi}$

za vse ξ ≥ 2657. Izpeljal je tudi sorodno mejo za število praštevil Čebišova ψ:

$|\psi(\xi)-\xi|<\frac{\sqrt \xi\,\ln^2 \xi}{8\pi}$

za vse ξ ≥ 73,2.

Logaritemski integral Li(ξ) je večji od π(ξ) za »majhne« vrednosti ξ. Vendar je Littlewood leta 1914 dokazal da temu ni vedno tako. Prva vrednost ξ za katero je π(ξ) večja od Li(ξ) je približno pri ξ = 1,397162914 · 10³¹⁶ (Demichel 2005). Takšna števila so znana kot Skewesova števila.

[uredi] Groba skica dokaza

V predavanju o praštevilih za širšo javnost je Tao, prejemnik Fieldsove medalje leta 2006, opisal pesniški pristop dokaza praštevilskega izreka s poslušanjem praštevilske »glasbe«. Začnemo z »zvočnim valovanjem«, ki je »glasno« pri praštevilih in tiho pri sestavljenih številih - to je von Mangoldtova aritmetična funkcija Λ(n), ki ni ne multiplikativna in ne aditivna. Potem analiziramo njegove note, oziroma frekvence, s procesom, sorodnim Fourierjevi transformaciji - to je Mellinova transformacija. Potem dokažemo, kar je težek del, da se določene »note« v glasbi ne morejo pojaviti. Ta izključitev določenih not vodi do praštevilskega izreka. Po Tau ta dokaz vodi do bolj globljega vpogleda v porazdelitev praštevil kot elementarni dokazi, opisani zgoraj ^[7].

[uredi] Teorija Dirichletovih vrst

Riemannova funkcija $ζ$ je določena tudi z Dirichletovo vrsto, kjer je $ζ(s)$ prototip, ki generira konstantno aritmetično funkcijo $f (n) = 1$ za vse n:

$\zeta(s) = \sum_{n=1}^{\infty} f(n) {1\over n^{s}} \; .$

Kvadrat Euler-Riemannove funkcije $ζ(s)$ generira funkcijo število deliteljev $τ(n)$ :

$\zeta(s)^{2} = \sum_{n=1}^{\infty} {\tau(n)\over n^{s}} \; .$

Obratna vrednost Euler-Riemannove funkcije $ζ(s)$ generira Möbiusovo aritmetično funkcijo $μ(n)$ :

${1\over\zeta(s)} = \sum_{n=1}^{\infty} {\mu(n)\over n^{s}} \;$

ali Mertensovo funkcijo:

$\frac{1}{\zeta(s)} = s \int_1^{\infty} \frac{M(x)}{x^{s+1}} dx \; .$

V splošnem velja, da če dve Dirichletovi vrsti $L (s,χ)$ in $M (s,χ)$ generirata aritmetični funkciji $f (n)$ in $g (n)$ , potem njun produkt $f (n) g (n)$ generira novo aritmetično funkcijo:

${h(n)} = \sum_{d\mid n} f(d) g\left({n\over d}\right) \; ,$

in se imenuje Dirichletov produkt dveh aritmetičnih funkcij $f (n)$ in $g (n)$ . Dirichletov produkt dobimo, če pomnožimo dve Dirichletovi vrsti in preuredimo člene:

$L(s,\chi)M(s,\chi) = \sum_{n=1}^{\infty} {f(n)\over n^{s}} \sum_{m=1}^{\infty} {g(m)\over m^{s}} =$

$\qquad\qquad\qquad\;\; = \sum_{n=1}^{\infty} \sum_{m=1}^{\infty} {f(n)g(m)\over (n m)^{s}} = \sum_{k=1}^{\infty} {h(k)\over k^{s}} \; ,$

kjer je:

$h(k) = \sum_{nm=k} f(n)g(m) = \sum_{d\mid k} f(d) g\left({k\over d}\right) \; .$

Enačba velja kadar vrsti $L (s,χ)$ in $M (s,χ)$ absolutno konvergirata. S produktom Dirichletovih vrst lahko generiramo veliko aritmetičnih funkcij v multiplikativni teoriji števil. Na primer:

${\zeta(s-1)\over \zeta(s)} = \sum_{n=1}^{\infty} {\varphi(n)\over n^{s}}$

in

$\zeta(s)\zeta(s-\alpha) = \sum_{n=1}^{\infty} {\sigma_{\alpha}(n)\over n^{s}} \; .$

V aditivni teoriji števil za generativne funkcije uporabimo raje potenčne vrste. Funkcija $A (χ)$ z razvitjem v potenčno vrsto:

$A(\chi) = \sum_{n=0}^{\infty} a(n) {\chi}^{n}$

generira koeficiente $a (n)$ . Če $B (χ)$ generira koeficiente $b (m)$ tako, da je:

$B(\chi) = \sum_{m=0}^{\infty} b(m) {\chi}^{m} \; ,$

potem je za vse tiste $χ$ , za katere obe vrsti absolutno konvergirata, njun produkt:

$A(\chi) B(\chi) = \sum_{n=0}^{\infty} a(n) {\chi}^{n} \sum_{m=0}^{\infty} b(m) {\chi}^{m} = \sum_{n=0}^{\infty} \sum_{m=0}^{\infty} a(n) b(m) {\chi}^{n+m} = \sum_{k=0}^{\infty} c(k) {\chi}^{k} \; ,$

kjer je:

$c(k) = \sum_{n+m=k}^{\infty} a(n) b(m) \; .$

Novo zaporedje se imenuje Cauchyjev produkt dveh zaporedij $a (n)$ in $b (m)$ . Na primer naj je $a (n) = 1$ , če je n kvadrat, drugače pa $a (n) = 0$ , tako, da je:

$A(\chi) = 1 + \chi + \chi^{4} + \chi^{9} + \chi^{16} + ... + \chi^{n^2} + ... \; .$

Tako $A (χ)$ vsebuje člene, ki so kvadrati. Kvadrat $A (χ)$ je dan z vrsto:

$A(\chi)^{2} = 1 + 2\chi + \chi^{2} + 2\chi^{4} + 2\chi^{5} + \chi^{8} + 2\chi^{9} + ... + b(n)\chi^{n} + ... \; ,$

kjer je $b (n)$ število načinov, s katerimi lahko izrazimo n kot vsoto dveh kvadratov pozitivnih celih števil, če upoštevamo vrstni red seštevancev. Četrta potenca pa je:

$A(\chi)^{4} = 1 + 4\chi + 6\chi^{2} + 4\chi^{3} + 5\chi^{4} + 12\chi^{5} + ... + c(n)\chi^{n} + ... \; ,$

kjer je $c (n)$ število načinov, s katerimi lahko izrazimo n kot vsoto štirih kvadratov pozitivnih celih števil. Obstaja, na primer, natanko 6 načinov, da zapišemo 2 kot vsoto štirih pozitivnih kvadratov:

$2 = 1+1+0+0 = 1+0+1+0 = 1+0+0+1 = 0+1+0+1 = 0+1+1+0 = 0+0+1+1 \; ,$

zato je $c (2) = 6$ . Euler je opazil, da je Lagrangeev izrek štirih kvadratov enakovreden izjavi, da je $c (n)$ pozitiven za vsak n, ni pa uspel dokazati, da je $c (n) > 0$ . Če so dovoljeni za seštevance tudi kvadrati negativnih celih števil, je število predstavitev celega števila kot vsota kvadratov precej večje. Če so, na primer, dovoljeni kvadrati -1, obstaja 24 različnih načnov zapisa 2 kot vsote štirih kvadratov. Število predstavitev celega števila n kot vsote k kvadratov celih števil (pozitivnih, negativnih ali ničle) označimo z $r k (n)$ . Njegova generativna funkcija je:

$\Theta(\chi)^{k} = 1 + \sum_{n=1}^{\infty} r_{k}(n) {\chi}^{n} \; ,$

kjer je funkcija $Θ(χ)$ določena z neskončno vrsto:

$\Theta(\chi) = \sum_{m=-\infty}^{\infty} {\chi}^{m^2} \; .$

Za primer $r 2 (n)$ glej zgoraj. Jacobi je pokazal, da lastnosti funkcije $Θ(χ)$ vodijo k podatkom, ki se nanašajo na predstavitve celih števil s kvadrati. Jacobijeva enačba iz teorije eliptičnih funkcij:

$\Theta(\chi)^{2} = 1 + 4\sum_{n=1}^{\infty} \left\lbrace \tau_{1}(n) - \tau_{3}(n)\right\rbrace {\chi}^{n} \; ,$

kjer sta $τ 1 (n)$ in $τ 3 (n)$ število deliteljev n kongruentno 1 in 3 po modulu 4. Če primerjamo koeficient $χ n$ v tej enačbi s koeficientom $χ n$ v generativni funkciji za $r 2 (n)$ , dobimo eksplicitno enačbo za število predstavitev n kot vsote dveh kvadratov:

$r_{2}(n) = 4\left\lbrace \tau_{1}(n) - \tau_{3}(n)\right\rbrace \; .$

S podobnimi postopki je Jacobi pokazal, da je $r 2 (n) = 8σ(n)$ , če je n sod in $r 4 (n)$ = 24-krat vsota sodih deliteljev n, če je n lih. Podobne enačbe $r k (n)$ za $k = 6,8,10$ in 12 so dobili na podoben nančin, vendar so bolj zapleteni. Enačbe za $r k (n)$ so znane za vse lihe $k \le 24$ . Za sode k je enačbe težje dobiti.

[uredi] Elementarni dokazi

V začetku 20. stoletja so dokaz poenostavili Landau in drugi matematiki. V prvi polovici 20. stoletja je nekaj matematikov verjelo, da obstaja hierarhija tehnik v matematiki in da je praštevilski izrek »globok« izrek, za katerega dokaz je potrebna kompleksna analiza. Metode s samo realnimi spremenljivkami niso veljale za ustrezne. Hardy je bil znan član te skupine [1].

Formulacijo tega prepričanja je deloma omajal dokaz praštevilskega izreka, ki je temeljil na Wienrovem tauberskem izreku iz teorije divergentnih vrst iz leta 1932, čeprav bi bilo moč označiti »globino« Wienrovega izreka kot enako metodam kompleksne analize. Predstava »elementarnega dokaza« v teoriji števil ni natančno določena, vendar se zdi da po navadi v grobem ustreza dokazom, ki jih je moč izvesti v Peanovi aritmetiki, in ne v močnejših teorijah kot je na primer aritmetika drugega reda. Obstajajo izjave Peanove aritmetike, ki jih je moč dokazati v aritmetiki drugega reda, ne pa v aritmetiki prvega reda. Takšen zgled je na primer Paris-Harringtonov izrek. Drugače pa so v praksi takšni izreki redki.

Selberg je našel elementarni dokaz praštevilskega izreka leta 1949, ki je uporabljal le prijeme iz teorije števil. Erdös je skoraj istočasno uporabil njegove zamisli in razdelal malo drugačen elementarni dokaz. Selbergovo delo je umirilo pojem »globine« za praštevilski izrek, in je pokazalo da so tehnično »elementarne« metode (oziroma Peanova aritmetika) močnejše kot so sprva pričakovali. Leta 1956 Gordon dokazal praštevilski izrek s pomočjo Stirlingove aproksimacije za velike $n!$ . Leta 2001 je Sudac pokazal, da je moč praštevilski izrek dokazati v primitivno rekurzivni aritmetiki^[8], veliko šibkejši teoriji kot je Peanova aritmetika.

Avigad in sodelavci so leta 2005 napisali računalniško različico tega elementarnega dokaza v interaktivnem sestavu dokazovanja izrekov Isabelle ^[9].

[uredi] Praštevilski izrek za aritmetična zaporedja

Naj $π k, a (ξ)$ označuje število praštevil v aritmetičnem zaporedju a, a + k, a + 2k, a + 3k, … manjše od ξ. Dirichlet in Legendre sta domnevala in de la Vallée Poussin dokazal, da če sta a in k tuji, potem velja:

$\pi_{k,a}(\xi) \sim \frac{1}{\phi(k)}\mathrm{Li}(\xi),$

kjer je φ(·) Eulerjeva funkcija φ. Praštevila so porazdeljena enakomerno med razredi ostankov [a] modulo k z gcd(a, k) = 1. To je moč dokazati s podobno metodo, ki jo je uporabil Newman za svoj dokaz praštevilskega izreka^[10].

Littlewood je leta 1914 pokazal da se predznak za funkcijo:

$\pi_{1,4}(\xi) - \pi_{3,4}(\xi) \,\!$

neskončnokrat spremeni.

[uredi] Domene funkcije števila praštevil

Praštevilski izrek je asimptotičen rezultat. Zaradi tega ga ne moremo uporabiti za določitev domene π(ξ).

Znane pa so nekatere meje definicijskega območja za π(ξ), kot je na primer Dusartova:

$\frac{\xi}{\ln \xi}\left(1+\frac{1}{\ln \xi}\right) < \pi(\xi) < \frac{\xi}{\ln \xi}\left(1+\frac{1}{\ln \xi}+\frac{2,51}{(\ln \xi)^2}\right) \; .$

Prva neenakost velja za vse ξ ≥ 599, druga pa za vse ξ ≥ 355991^[11].

Šibkejša, vendar včasih uporabna meja je:

$\frac {\xi}{\ln \xi + 2} < \pi(\xi) < \frac {\xi}{\ln \xi - 4} \!\,$

za ξ ≥ 55^[12].

V Dusarovi disertaciji je moč najti malce močnejšo različico takšne neenakosti, ki velja za velike ξ.

[uredi] Približki za n-to praštevilo

Kot posledica praštevilskega izreka izhaja asimptotičen izraz za n-to praštevilo, označen kot p_n:

$p_n \sim n \ln n \; .$

Boljši približek je:

$p_n = n \ln n + n \ln \ln n + \frac{n}{\ln n} \big( \ln \ln n - \ln n- 2 \big) + O\left( \frac {n (\ln \ln n)^2} {(\ln n)^2}\right).$ ^[13]

Rosserjev izrek pravi da je p_n večji od n ln n. To je moč izboljšati z naslednjim parom mej^[14]:

$n \ln n + n(\ln\ln n - 1) < p_n < n \ln n + n \ln \ln n \quad\mbox{za } n \ge 6 \; .$

Leva neenakost je Dusartova^[15] in velja za n ≥ 2.

[uredi] Podobnost za nerazcepne polinome v končnem obsegu

Obstaja podobna oblika praštevilskega izreka, ki opisuje »porazdelitev« nerazcepnih polinomov v končnem obsegu. Ta oblika je na vso moč podobna klasičnemu praštevilskemu izreku.

Naj je F = GF(q) končni obseg s številom elementov q, za poljubni q in naj je N_n število nerazcepnih polinomov 1. reda v F, katerega stopnja je enaka n. Iščemo takšne polinome s koeficienti izbranimi iz F, ki jih ne moremo zapisati kot produkte polinomov manjše stopnje. V tem primeru ti polinomi igrajo vlogo praštevil, saj so vsi polinomi 1. reda sestavljeni iz njihovih produktov. Pokazati je moč, da velja:

$N_n \sim \frac{q^n}{n} \; .$

Če pišemo ξ = qⁿ, potem je desna stran enaka:

$\frac{\xi}{\log_q \xi} \; ,$

kjer je podobnost bolj vidna. Ker obstaja natanko qⁿ polinomov 1. reda stopnje n (vključno z razcepnimi), lahko zgoraj zapisano povemo še drugače: če naključno izberemo polinom 1. reda stopnje n, potem je verjetnost da je nerazcepen enaka približno 1/n.

Podobno obliko ima Riemannova domneva:

$N_n = \frac{q^n}n + O\left(\frac{q^{n/2}}{n}\right) \; .$

Dokazi v takšnih oblikah so veliko preprostejši od klasičnih. Premisliti je treba po kombinatorični poti. Vsak element stopnje n razširitve F je koren nekega nerazcepnega polinoma, katerega stopnja d deli n. S štetjem teh korenov na dva načina se izkaže, da velja:

$q^n = \sum_{d\mid n} d N_d \; ,$

kjer vsota poteka prek vseh deliteljev d od n. Möbiusov obrat potem vodi do:

$N_n = \frac1n \sum_{d\mid n} \mu(n/d) q^d \; ,$

kjer je μ(k) Möbiusova funkcija. To enačbo je poznal tudi Gauss. Glavni člen se pojavi pri d = n, in ni težko omejiti preostalih členov. Izjava »Riemannove domneve« je odvisna od dejstva, da največji pravi delitelj n ne more biti večji od n/2.

[uredi] Glej tudi

[uredi] Opombe

^ Število praštevil < 10^n (A006880). OEIS.
^ Razlika med pi(10^n) in celim številom, najbližjim k 10^n / log(10^n) (A057835). OEIS.
^ Razlika med Li(10^n) inPi(10^n), kjer je Li(x) - integral log(x) in Pi(x) - število praštevil <= x (A057752). OEIS.
^ Ingham, A.E. (1990). The Distribution of Prime Numbers. Cambridge University Press, 2-5. ISBN 0-521-39789-8.
^ Helge von Koch (Dec 1901). »Sur la distribution des nombres premiers«. Acta Mathematica 24 (1): 159-182.
^ Lowell Schoenfeld (april 1976). »Sharper Bounds for the Chebyshev Functions θ(x) and ψ(x), II«. Mathematics of Computation 30 (134): 337–360.
^ Video in prosojnice Taojevega predavanja o praštevilih, UCLA, januar 2007.
^ Olivier Sudac (april 2001). »The prime number theorem is PRA-provable«. Theoretical Computer Science 257 (1–2): 185-239.
^ Jeremy Avigad, Kevin Donnelly, David Gray, Paul Raff (2005). »A formally verified proof of the prime number theorem«. e-print cs. AI/0509025 v ArXiv.
^ Ivan Soprounov (1998). »A short proof of the Prime Number Theorem for arithmetic progressions«.
^ Pierre Dusart, Autour de la fonction qui compte le nombre de nombres premiers, doktorska teza za l'Université de Limoges (1998).
^ Barkley Rosser (januar 1941). »Explicit Bounds for Some Functions of Prime Numbers«. American Journal of Mathematics 63 (1): 211-232.
^ Michele Cipolla (1902). »La determinazione assintotica dell'n^imo numero primo«. Matematiche Napoli 3: 132-166.
^ Eric Bach, Jeffrey Shallit (1996). Algorithmic Number Theory. MIT Press. ISBN 0-262-02405-5.
^ Pierre Dusart (1999). »The kth prime is greater than k(ln k + ln ln k-1) for k>=2«. Mathematics of Computation 68.

[uredi] Viri

[1] Andrew Granville, Harald Cramér and the distribution of prime numbers, Scandinavian Actuarial Journal, vol. 1, str. 12–28, 1995. (postscript).
[2] Ilan Vardi, An introduction to Analytic Number Theory, 1998.

[uredi] Zunanje povezave

Razpredelnica praštevil Antona Felkela (v angleščini)
Praštevilske enačbe in Praštevilski izrek na MathWorld (v angleščini)
Praštevilski izrek na PlanetMath (v angleščini)
How Many Primes Are There? in The Gaps between Primes, Chris Caldwell, Univerza Tennesseeja v Martinu (University of Tennessee at Martin) (v angleščini)
Preglednice funkcij števil praštevil, Tomás Oliveira e Silva (v angleščini)

[_note_0] Število praštevil < 10^n (A006880). OEIS.

[_note_1] Razlika med pi(10^n) in celim številom, najbližjim k 10^n / log(10^n) (A057835). OEIS.

[_note_2] Razlika med Li(10^n) inPi(10^n), kjer je Li(x) - integral log(x) in Pi(x) - število praštevil <= x (A057752). OEIS.

[_note_3] Ingham, A.E. (1990). The Distribution of Prime Numbers. Cambridge University Press, 2-5. ISBN 0-521-39789-8.

[_note_4] Helge von Koch (Dec 1901). »Sur la distribution des nombres premiers«. Acta Mathematica 24 (1): 159-182.

[_note_5] Lowell Schoenfeld (april 1976). »Sharper Bounds for the Chebyshev Functions θ(x) and ψ(x), II«. Mathematics of Computation 30 (134): 337–360.

[_note_6] Video in prosojnice Taojevega predavanja o praštevilih, UCLA, januar 2007.

[_note_7] Olivier Sudac (april 2001). »The prime number theorem is PRA-provable«. Theoretical Computer Science 257 (1–2): 185-239.

[_note_8] Jeremy Avigad, Kevin Donnelly, David Gray, Paul Raff (2005). »A formally verified proof of the prime number theorem«. e-print cs. AI/0509025 v ArXiv.

[_note_9] Ivan Soprounov (1998). »A short proof of the Prime Number Theorem for arithmetic progressions«.

[_note_10] Pierre Dusart, Autour de la fonction qui compte le nombre de nombres premiers, doktorska teza za l'Université de Limoges (1998).

[_note_11] Barkley Rosser (januar 1941). »Explicit Bounds for Some Functions of Prime Numbers«. American Journal of Mathematics 63 (1): 211-232.

[_note_12] Michele Cipolla (1902). »La determinazione assintotica dell'n^imo numero primo«. Matematiche Napoli 3: 132-166.

[_note_13] Eric Bach, Jeffrey Shallit (1996). Algorithmic Number Theory. MIT Press. ISBN 0-262-02405-5.

[_note_14] Pierre Dusart (1999). »The kth prime is greater than k(ln k + ln ln k-1) for k>=2«. Mathematics of Computation 68.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]