O notacija

Primer notacije O: f(x) ∈ O(g(x)) za c > 0 (e.g. c = 1) in x₀ (e.g. x₀ = 5) tako, da je f(x) < cg(x) kadar je x > x₀.

O notacija (tudi notacija veliki O) se v matematiki uporablja za opisovanje limitnega obnašanja funkcije, ko argument gre proti določeni vrednosti ali neskončnosti. Ta notacija pripada večji družini notacij, ki jih imenujemo Landauova notacija, Bachmann-Landauova notacija (imenovana po Edmundu Landau (1877 – 1938) in Paulu Bachmannu (1837 - 1920)) ali asimptotska notacija.

V računalništvu se notacija O uporablja za razvrščanje algoritmov po tem kako se odzivajo na spremembe v velikosti vhoda.

Definicija

Naj bosta f(x) in g(x) dve funkciji, ki sta definirani nad neko podmnožico realnih števil. Lahko zapišemo :

$f(x)=O(g(x))\text{ ko gre }x\to\infty\,$

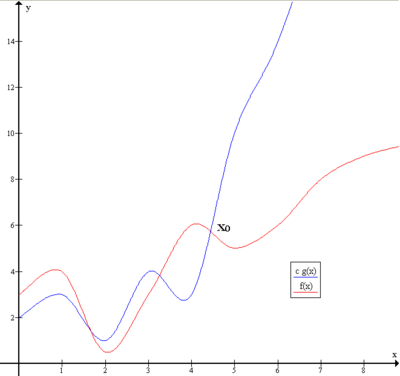
Če in samo, če obstoja pozitivna konstanta M tako, da je za vse dovolj velike vrednosti x , je f(x) kvečjemu z M pomnožen z g(x) v absolutno vrednost. To je f(x) = O(g(x)) samo, če in samo če obstoja pozitivno realno število M in realno število x₀, da velja

$|f(x)| \le \; M |g(x)|\text{ za vse }x>x_0$.

V mnogih primerih je predpostavka, da nas zanima samo stopnja rasti ko gre x proti neskončnosti, neveljavna. Običajno zapišemo f(x) = O(g(x)). Označevanje se lahko uporabi za prikaz obnašanja funkcije f blizu nekega realnega števila (pogosto okoli a=0). Lahko zapišemo, da je

$f(x)=O(g(x))\text{ kadar gre }x\to a\,$

če in samo, če obstoja takšni pozitivni števili δ in M, da velja

$|f(x)| \le \; M |g(x)|\text{ za }|x - a| < \delta$.

Če je g(x) neničelen za vrednosti dovolj blizu vrednosti a se lahko obe od teh definicij združita z uporabo zgornje in spodnje limite

$f(x)=O(g(x))\text{ kadar gre }x \to a\,$

če in samo, če je

$\limsup_{x\to a} \left|\frac{f(x)}{g(x)}\right| < \infty$.

Skupina Bachmann-Landauovih notacij

notacija	ime	opis	definicija: za dovolj velike $n$...	definicija	opombe
$f(n) \in O(g(n))$	veliki omikron; veliki O; veliki Oh	$f$ je omejena zgoraj z $g$ (do konstantnega faktorja) asimptotično	$|f(n)| \leq g(n)\cdot k$ za neki k	$\exists k>0 \; \exists n_0 \; \forall n>n_0 \; |f(n)| \leq |g(n)\cdot k|$ or $\exists k>0 \; \exists n_0 \; \forall n>n_0 \; f(n) \leq g(n)\cdot k$
$f(n) \in \omega(g(n))$	veliki omega	$f$ je omejen spodaj z $g$ (do konstatnega faktorja) asimptotično	$f(n) \geq g(n)\cdot k$ za pozitivni k	$\exists k>0 \; \exists n_0 \; \forall n>n_0 \; g(n)\cdot k \leq f(n)$	od začetka 20. stoletja so dokumenti o teoriji števil so stalno bolj uporabljali to notacijo, vendar z občutkom, da je f = o(g) napačno.
$f(n) \in \theta(g(n))$	veliki theta	$f$ je omejen zgoraj in spodaj z $g$ asimptotično	$g(n)\cdot k_1 \leq f(n) \leq g(n)\cdot k_2$ za neki pozitivni k1, k2	$\exists k_1>0 \; \exists k_2>0 \; \exists n_0 \; \forall n>n_0$ $g(n) \cdot k_1 \leq f(n) \leq g(n) \cdot k_2$
$f(n) \in o(g(n))$	mali omikron; mali O; mali Oh	$f$ prevladuje $g$ asimptotično	$|f(n)| \le |g(n)|\cdot \varepsilon$ za vsak $\varepsilon$	$\forall \varepsilon>0 \; \exists n_0 \; \forall n>n_0 \; |f(n)| \le |g(n)\cdot \varepsilon|$
$f(n) \in \omega(g(n))$	mali omega	$f$ prevladuje $g$ asimptotsko	$f(n) \ge g(n)\cdot k$ za vsak k	$\forall k>0 \; \exists n_0 \; \forall n>n_0 \; g(n)\cdot k < f(n)$
$f(n)\sim g(n)\!$	On the order of	$f$ je enak $g$ asimptotsko	$f(n)/g(n) \to 1$	$\forall \varepsilon>0\;\exists n_0\;\forall n>n_0\;\left|{f(n) \over g(n)}-1\right|<\varepsilon$

Bachmann–Landauova notacija uporablja nekaj mnemotehnik. Tako lahko preberemo "omikron" kot "o-mikron" in "omega" lahko preberemo kot "o-mega".

• mnemotehnika za o-micron: Čitanje o-mikron $f(n) \in O(g(n))$ in $f(n) \in o(g(n))$ si lahko mislimo kot "O-manjši kot" in "o-manjši kot". Ta mnemotehnika micro/manjši se nanaša na dovolj velik vhodni parameter ali parametre, $f$ raste po stopnji, ki je manjša kot $cg$ glede na $g \in O(f)$ or $g \in o(f)$.
• mnemotehnika za o-mega : Čitanje o-mega $f(n) \in \Omega(g(n))$ in $f(n) \in \omega(g(n))$ si lahko mislimo kot "O-večji kot". Ta mnemotehnika mega/večji: se nanaša na dovolj velik vhodni parameter ali parametre, $f$ raste po stopnji, ki je večja kot $cg$ glede na $g \in \Omega(f)$ ali $g \in \omega(f)$.
• mnemotehnika za zgornji znak: Ta mnemotehnika nas spominja na to, kdaj uporabimo zgornje grške črke v $f(n) \in O(g(n))$ in $f(n) \in \Omega(g(n))$: za dovolj velik vhodni parameter ali parametre, $f$ raste po stopnji, ki bi lahko bila enaka z $cg$ glede na $g \in O(f)$.
• mnemotehnika za spodnji znak: Ta mnemotehnika nas spominja na to, kdaj moramo uporabiti male grške črke v $f(n) \in o(g(n))$ in $f(n) \in \omega(g(n))$: za dovolj velik vhodni parameter ali parametre, $f$ raste po stopnji, ki je neenaka z $cg$ glede na $g \in O(f)$.

Razen notacije O se v računalništvu uporablja še notacija z velikim teta (Θ) in velikim omega (Ω) . V računalništvu pa se zelo redko uporablja notacija z uporabo malega omega (ω).

Zunanje povezave

• Notacija „veliki O“ na MaFiRa (v slovenščini)
• Uvod v asimptotske notacije (v angleščini)
• Landauovi simboli na MathWorld (v angleščini)