Ničla funkcije
Ničla funkcije f je v matematiki tisto število x, pri katerem je vrednost funkcije f enaka 0. Torej ničlo funkcije poiščemo tako, da rešimo enačbo:
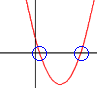
Na grafu ničli ustreza presečišče z abscisno osjo.
Stopnja ničle[uredi | uredi kodo]
Pri polinomih lahko govorimo tudi o stopnji ničle. Rečemo, da je število x0 ničla stopnje k, če se da polinom p zapisati kot
- , kjer je .

Ločimo naslednje tipe ničel:
- Ničle stopnje 1 imenujemo tudi enostavne ničle. V enostavni ničli graf polinoma seka abscisno os pod določenim neničelnim kotom.
- Ničle stopnje 2, 4, 6, itd (tj. dvojne, štirikratne, šestkratne ničle itd) imenujemo tudi ničle sode stopnje. V teh ničlah se graf polinoma dotika abscisne osi, vendar je ne prečka. V ničli sode stopnje je vedno tudi lokalni ekstrem funkcije.
- Ničle stopnje 3, 5, 7, itd (tj. trojne, petkratne, sedemkratne ničle itd) imenujemo tudi ničle višje lihe stopnje. V teh ničlah se graf polinoma zelo dobro prilega abscisni osi, jo pa tudi prečka. V ničli višje lihe stopnje stopnje je vedno tudi vodoravni prevoj (tj. prevoj v katerem je tangenta vodoravna).
V ničli k-te stopnje (k>1) velja, da so tudi nekateri odvodi enaki 0:
To značilnost uporabimo kot definicijo stopnje ničle v splošnem.




