Aristarh
| Aristarh s Samosa Αρίσταρχος ὁ Σάμιος | |
|---|---|
 Kip Aristarha na Aristotelovi univerzi v Solunu | |
| Rojstvo | cca. 310 pr. n. št.[1] Samos[1] |
| Smrt | cca. 230 pr. n. št.[1] Aleksandrija |
| Državljanstvo | Samos |
| Poklic | astronom |
Aristarh [aristárh] (starogrško Αρίσταρχος ὁ Σάμιος: Arístarhos hó Sámios), starogrški astronom in matematik, * 310 pr. n. št., otok Samos, Jonija, Grčija, † okoli 230 pr. n. št., Aleksandrija.
Po vsej verjetnosti je bil Aristarh prvi astronom, ki je predlagal, da Zemlja kroži okrog Sonca in, da so planeti podobni Zemlji in prav tako krožijo okrog Sonca. Njegove astronomske zamisli niso z lahkoto sprejemali in so bile nepomembne v primeri z Aristotelovimi in Ptolemajevimi. V celoti so jih sprejeli v Kopernikovem času skoraj 2000 let pozneje.
Že mlad je prišel v Aleksandrijo. Bil je Stratonov učenec. Prvi je postavil domnevo, da je Sonce središče Vesolja, zaradi česar so ga obtožili brezboštva in ga izgnali iz Aten.
Heliocentrizem[uredi | uredi kodo]
Edino Aristarhovo delo, ki se je ohranilo do danes O velikostih in razdaljah [Sonca in Lune] (Περὶ μεγεθῶν καὶ ἀποστημάτων [ἡλίου καὶ σελήνης]), temelji na geocentričnem modelu. Preko navedb drugih avtorjev pa se ve, da je Aristarh napisal še drugo knjigo, kjer je predlagal še domnevo heliocentričnega modela. Arhimed je v delu Peščeni račun (Ψαμμίτης) zapisal:
- »Ti, kralj Gelon se zavedaš in veš, da večina astronomov označuje 'vesoljstvo' kot kroglo, katere središče sovpada s središčem Zemlje, njen polmer pa je enak ravni črti, ki povezuje središči Sonca in Zemlje. To je obče mnenje kot si slišal od astronomov in tako navajajo v svojih spisih. Vendar je Aristarh privlekel na dan knjigo, ki vsebuje določene različne domneve z risbami, kjer se kot posledica vzetih predpostavk zdi, da je vesoljstvo precej večje od ravnokar omenjenega. V njegovih domnevah zvezde stalnice in Sonce ostajajo nepomični, Zemlja se giblje okrog Sonca po obsegu kroga, Sonce leži v središču njenega tira in krogla nepomičnih zvezd, ki leži v istem središču kot Sonce, je tako velika, da je krog v katerem predpostavlja Zemljino kroženje v takem sorazmerju z razdaljo nepomičnih zvezd kot središče krogle, s to površino.«
Aristarh je tako verjel, da so zvezde neskončno daleč. To je podkrepil z opažanjem, da ni nobene vidne paralakse, opazovanega gibanja zvezd glede druge na drugo med gibanjem Zemlje okrog Sonca. Zvezde so v resnici veliko dlje kot so menili v antiki, saj se zvezdno paralakso lahko zazna le z daljnogledi. Geocentrični model je imel enostavnejšo in boljšo razlago za nepojavljanje paralakse. Zavračanje heliocentričnega pogleda je bilo navidezno kar možno, kar nakazuje naslednji odlomek Plutarhovega besedila (O navideznem videzu Lunine krogle):
- »Lucij (Lucius) se je nasmehnil in rekel: 'Moj dragi, samo ne obtoži nas pred sodiščem zaradi brezboštva, kot je Kleant, [Aristarhov sodobnik] mislil, da je dolžnost starih Grkov obtožiti Aristarha iz Samosa zaradi brezbožnosti, ker je pognal v gibanje Srce vesolja [to je Zemljo]' Aristarh je namreč poskusil rešiti opazovano s privzetkom, da nebo stalnic in nebesa mirujejo, Zemlja pa se giblje po poševnem krogu, poleg tega pa se istočasno še vrti okrog lastne osi. Kar nas zadeva, ne postavljamo nobene trditve. Toda ali nekdo, ki razglaša, da je Luna podobna Zemlji, moj dragi, ne obrača spodnjega navzgor bolj kot vi? Zemljo pustite prosto lebdeti v zraku, čeprav je veliko večja kot Luna. Kot je znano, merijo astronomi njeno velikost pri Luninem mrku ob prehodu skozi zemeljsko senco po času, ko se mudi v njej'.«

Lahko, da je na osnovi sicer dokaj netočnih izidov Aristarh sklepal, da manjša Zemlja kroži okrog Sonca, kot manjša Luna kroži okrog Zemlje, in ne obratno, saj je bil mnenja, da mora vedno manjše telo krožiti okrog večjega. Na osnovi tega je zagovarjal heliocentrično sliko, za katero pa je bilo še prezgodaj, čeprav so jo še pred njim predlagali Filolaj, Hiket, Ekfant in Heraklit Pontski. Leta 260 pr. n. št. je tako pokazal, da se lahko gibanja nebesnih teles preprosto pojasni, če se vzame, da vsi planeti skupaj z Zemljo krožijo okrog Sonca. Zdelo se je, da zvezde mirujejo, če se izvzame njihovo navidezno gibanje zaradi vrtenja Zemlje. Zato je sklepal, da so od Zemlje tudi neskončno oddaljene. Zaradi teh pogledov je bil znan kot antični Kopernik. Zdi se, da je Kopernik poznal njegove zamisli, ker jih je omenil v odstavku, ki ga je pozneje umaknil iz svoje knjige, ker morda ni hotel zbuditi dvomov v svojo izvirnost.
V svojem omenjenem delu je Aristarh podal metodo s katero se te količine računa. Njegova metoda je bila v bistvu pravilna, vendar so bile njegove izračunane vrednosti zaradi njegovega pomanjkljivega matematičnega znanja in zaradi premalo točnih inštrumentov napačne. Poskušal je povezati astronomska opazovanja in računanje. Iz izidov pri računanju je izpeljal sklep, na katerem je zgradil svojo osnovno zamisel. To je bil drug zgodnji zgled za medsebojni vpliv merjenja in računanja. V resnici so bili njegovi podatki grobi in bi sedaj veljali bolj za ocene. Vseeno pa se sme v njegovem dokaj osamljenem prizadevanju videti vmesni korak na poti od kakovostnega pogleda do točnega računanja. Izhajal je od privzetkov in podatkov:
- Luna dobi svetlobo od Sonca in jo odbija,
- Zemlja je kot točka v središču krogle, po kateri se giblje Luna,
- ko je ob prvem ali zadnjem krajcu Luna polovično osvetljena, je krog v smeri opazovalčevega očesa na Zemlji.
- razdalja Lune od Zemlje, ko se zdi Luna razpolovljena, je za 1/30 manjša od kvadranta (aL / rZ = 29),
- širina Zemljine sence je enaka 2. Lunama, rZ / rL = 2 in
- Luna meri 1/15 živalskega kroga.
Velikost Lune[uredi | uredi kodo]
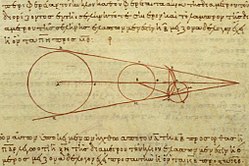
Aristarh je opazoval gibanje Lune skozi Zemljino senco med Luninim mrkom. Ocenil je, da je premer Zemlje enak 3 kratnemu premeru Lune. Z uporabo Eratostenovega izračuna velikosti obsega Zemlje (42000 km), je zaključil, da je obseg Lune 14.000 km. V resnici je njen obseg približno 10.916 km.
Razdalja med Zemljo in Soncem (astronomska enota)[uredi | uredi kodo]
Trdil je, da je čas od prvega do zadnjega krajca Lune za 1 dan krajši kot čas od zadnjega krajca do prvega. Pri obhodni dobi Lune približno 27 dni sta oba dela v razmerju 13/14. Sklepal je, da Sonce, Luna in Zemlja v trenutnku prvega ali zadnjega krajca Lune tvorijo skoraj pravokotni trikotnik. Topi kot pravokotnega trikotnika s Soncem, Zemlji in Luno v ogliščih meri:
- α = 13 / (13 + 14) · 2) · 360° = 86,7° .
To se ujema s 4. postavko: 90 - 90°/30 = 87°. Iz tega je okoli leta 265 pr. n. št. z uporabo pravilne geometrije, vendar z napačnimi opazovalnimi podatki, skušal izmeriti astronomsko enoto in videl, da sta oddaljenosti Sonca in Lune v razmerju od 18 do 20. Danes se izračuna aS / aL = 1 / cos 87° = 19.
S tem se je močno zmotil, vendar se mu tega ne sme zameriti, saj je meritev še danes dokaj zahtevna, ker se težko ugotovi trenutek, ko je Luna ravno polovično osvetljena. Današnja meritev da 24-krat manjšo razliko, to je približno 1 uro. Tako meri kot 89,87° = 89° 52' 12" in je aS / aL = 430. Za astronomsko enoto je dobil oceno 560:
- aS / rZ = 19 / (2 tan 1°) = 544,3 ,
kar je bila prehuda napaka, ki je zavedla pozneje celo Hiparha, ker je ni preverjal.
Pokazal je, da imata Luna in Sonce skoraj enaki navidezni kotni velikosti (φ ≈ 1/2°) in morata biti zaradi tega njuna premera v sorazmerju z njunima razdaljama od Zemlje.[2] Tako je zaključil, da je Sonce 20-krat večje od Lune, kar je tudi napačno, vendar smiselno dosledno /logično/. Velikost Sonca je ocenil na 10 Zemljinih, rS / rZ = 9,5, če se vzame, da je njegova navidezna velikost približno enaka Lunini. Lunin polmer so primerjali z Zemljinim polmerom po času prehoda Lune skozi zemeljsko senco pri Luninem mrku. Aristarh naj bi pozneje 5. postavko še izboljšal na rZ / rL = 8 / 3.
Zadnja 6. postavka je izmerjena že kar malomarno, saj so tedaj kote v astronomiji merili veliko točneje. Zorni kot Luninega premera naj bi bil tako 2°, ker ima zodiak 12 nebesnih znamenj. Prava vrednost približno 1/2° je 4-krat manjša. Menda je pozneje uvidel svojo napako in jo popravil, kakor je navedel Arhimed.
O Aristarhovem pomembnem delu je pisal tudi Vitruvij v svoji razpravi O arhitekturi (De architetura):
- »Takšni možje so redki. Možje kot so bili v preteklosti Aristarh, Filolaj in Arhit iz Tarenta, Apolonij iz Perge, Eratosten iz Kiren, Arhimed in Skopinas iz Sirakuz. Potomcem so zapustili mnogo svojih izumljenih mehanskih in gnomonskih priprav, ter pojasnili njihovo uporabo z matematičnimi načeli.«
Seveda bi vsakdo vprašal kaj je Aristarh izumil. Vitruvij je pojasnil da je izumil sončno uro v obliki poloble posode s kazalcem na sredi, ki je delal sence.
Aristarh je vse premalo znan tudi kot matematik, ker ga po navadi navajajo samo kot nepraktičnega astronoma. Vendar so same njegove metode računanja verjetno še najbolj pomembne.
Dolgo leto in dolžina meseca[uredi | uredi kodo]
Arhimed in sodobni znanstveniki občudujejo Aristarha zaradi njegove daljnovidnosti o velikosti Vesolja. Aristarh je predlagal tudi najdaljšo časovno periodo antične Grčije, »dolgo leto« 4868 Sončevih let, v trajanju 270 sarojev po 18. Kalipovih let in 10 2/3 stopinj. Njegov cikel mrkov s 4267 meseci je navajal Ptolemaj kot izredno točen babilonski mesec, ki je bil točen pod sekundo, in so ga našli na klinopisnih tablicah iz časa malo pred letom 200 pr. n. št. Dolgo leto je vsebovalo dolžino meseca, ki se je ujemala z babilonsko vrednostjo na 1/10.000, desetletja prej preden so ga v Babiloniji sploh uporabljali. Aristarhovo delo predstavlja korak v znanosti v več ozirih. Prejšnje ocene dolžine meseca so imele napako 114 sekund (Meton, 432 pr. n. št.) in 22 sekund (Kalip, 330 pr. n. št.).
Precesija enakonočij[uredi | uredi kodo]
V Vatikanu sta se ohranila dva staroveška rokopisa z ocenami dolžine leta. Edini antični znanstvenik, ki je naveden, da je podal dve različni vrednosti, je Aristarh. Morda gre za najzgodnejši primer izrazov z verižnimi ulomki. S števili iz rokopisov je to moč točno izračunati. Vrednosti sta Aristarhovi leti 365 1/152 dni in 365 - 15/4868 dni, ki predstavljata siderično in meščansko leto, verjetno tropsko. Oba imenovalca se lahko poveže z Aristarhom, po katerem je bil poletni Sončev obrat 152 let po Metonovem, in njegovo dolgo leto je trajalo 4868 let. Razlika med sideričnim in tropskim letom je enaka precesiji enakonočij. Prva vrednost je točna na nekaj sekund, druga pa na nekaj minut. Obe sta blizu vrednostim, ki sta jih kasneje uporabljala Hiparh in Ptolemaj. Precesija je skoraj natanko 1 stopinjo na stoletje in malo premajhna. Na žalost so vrednost 1 stopinje na stoletje uporabljali kasnejši astronomi vse do arabskih. Pravilna vrednost v Aristarhovem času je bila približno 1,38° na stoletje.
Koledar[uredi | uredi kodo]
Nekateri viri nakazujejo, da je Aristarh razdelal julijanski koledar že nekako 200 let pred Sosigenom, ki je leta 46 pr. n. št. pomagal pri prenovi zastarelega grškega koledarja za časa Julija Cezarja, kar pa se zdi malo verjetno.
Poimenovanja[uredi | uredi kodo]

Po njem se imenuje udarni krater na Luni Aristarh s koordinatama 23,7° severno; 47,4° zahodno, premerom 40 km in globino 3,7 km, ter asteroid glavnega pasu 3999 Aristarh (3999 Aristarchus), ki ga je odkril Takuo Kodžima leta 1989. Po njem se imenuje tudi letališče na Samosu.
Glej tudi[uredi | uredi kodo]
Sklici[uredi | uredi kodo]
- ↑ 1,0 1,1 1,2 Biographical Encyclopedia of Astronomers — New York: Springer Science+Business Media, 2007. — ISBN 978-0-387-31022-0 — doi:10.1007/978-0-387-30400-7
- ↑ Likar (2018), str. 11.
Viri[uredi | uredi kodo]
- Likar, Andrej (2018), Prelomi v razvoju fizike, Matematika - fizika : zbirka univerzitetnih učbenikov in monografij, Ljubljana: DMFA - založništvo, str. 11–14, COBISS 296620288, ISBN 978-961-212-294-2, ISSN 1408-1571, OCLC 1080419421
- Strnad, Janez (2010), Fiziki, 7. del, Ljubljana: Modrijan, str. 13–28, COBISS 53716736, ISBN 978-961-241-424-5
Zunanje povezave[uredi | uredi kodo]
- Stran o Aristarhu Arhivirano 2005-05-11 na Wayback Machine. Univerze svetega Andreja (angleško)
