Lambertova funkcija W

Lambertova fúnkcija W [lámbertova ~ v] (tudi fúnkcija ω [~ ómega]) je v matematiki obratna funkcija:
kjer je ew naravna eksponentna funkcija in w kompleksno število. Imenuje se po Johannu Heinrichu Lambertu.
Tu je funkcija označena z W. To oznako sta prva uporabila Pólya in Szegő leta 1925. Za vsako kompleksno število z velja:
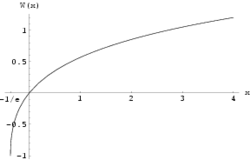
Ker funkcija f v (−∞, 0) ni injektivna, zavzame funkcija W v [−1/e, 0) več vrednosti. Če se omejimo na realne argumente x ≥ −1/e in zahtevamo w ≥ −1, je na ta način določena funkcija W0(x) z enoličnimi vrednostmi in njen graf je prikazan na sliki. Velja W0(0) = 0 in W0(−1/e) = −1.
Lambertove funkcije W ne moremo izraziti s členi elementarnih funkcij. Funkcija je uporabna v kombinatoriki, na primer pri preštevanju dreves. Z njo lahko rešimo različne enačbe, ki vsebujejo eksponente. Pojavlja se pri reševanju časovno zakasnelih diferencialnih enačb, kot je na primer y'(t) − a y(t − 1) = 0.
Odvajanje in integriranje[uredi | uredi kodo]
Z implicitnim odvajanjem je moč pokazati, da za W velja navadna diferencialna enačba:
in od tod odvod:
Funkcija W(x) in mnogo izrazov, ki vsebujejo W(x), se lahko integrirajo s substitucijo w = W(x), oziroma x = w ew:
Taylorjeva vrsta[uredi | uredi kodo]
Taylorjeva vrsta funkcije W0 okrog točke 0 se lahko izračuna z Lagrangeevim izrekom o obratu in je dana z:
Njen konvergenčni polmer je 1/e, kot se lahko vidi iz d'Alembertovega kriterija. Funkcijo, določeno s to vrsto, se lahko razširi v holomorfno funkcijo, ki je določena za vsa kompleksna števila z vejiščem vzdolž intervala (-∞, -1/e]. Ta holomorfna funkcija določa glavno vejitev Lambertove funkcije W.
Uporaba[uredi | uredi kodo]
S funkcijo se lahko reši več enačb, ki vsebujejo eksponente. V splošnem se dajo vsi členi z neznanko na eno stran enačbe, tako da ima obliko Y = XeX, v katere točki funkcija W da rešitev.
Z drugimi besedami :
Matematika[uredi | uredi kodo]
- Zgled 1
Bolj splošno se lahko enačba:
kjer je:
pretvori prek substitucije:
v:
kar da:
in končno rešitev:
- Zgled 2
Podobno se pokaže, da ima enačba:
rešitev:
ali enakovredno:
- Zgled 3
Če kompleksna neskončna eksponentna funkcija (tetracija):
konvergira, Lambertova funkcija W da dejansko vrednost limite:
kjer je ln z glavno vejišče funkcije kompleksnega logaritma.
- Zgled 4
Rešitve enačbe:
imajo obliko:
- Zgled 5
Asimptotična enačba za Bellova števila:
Fizika[uredi | uredi kodo]
- Zgled 6
Rešitev za tok v električnem tokokrogu zaporedno vezanih diod/upornikov se lahko zapiše s členi funkcije W. Glej modeliranje diod.
- Zgled 7
Časovno zakasnela diferencialna enačba:
ima karakteristično enačbo , kar vodi do in , kjer je indeks vejišča. Če je realen, je treba obravnavati le .
- Zgled 8[1]
Planckov zakon sevanja črnega telesa ima vrhove za:
kar določa Wienov zakon. Frekvence in valovne dolžine vrhov spektralnih gostot sevanja so različne za vsako temperaturo, in okrog njih telesa najmočneje sevajo.
- Zgled 9
Zrnati in naplavni tok front in naplavin, ter fronte viskoznih tekočin v naravnih pojavih kot tudi v laboratorijskih poskusih lahko opišemo z Lambert-Eulerjevo funkcijo omega:[2]
kjer je H(x) višina toka naplavin, x lega kanalskega toka, L poenoteni modelni parameter, ki ga sestavlja več fizikalnih in geometrijskih parametrov toka, višina toka in gradient hidravličnega tlaka.
- Zgled 10
Lambertova funkcija W je optimalna rešitev za potrebno magnetno polje Zeemanovega zaviralnika.[3]
Tehnologija preoblikovanja[uredi | uredi kodo]
- Zgled 11
Sila preoblikovanja kovine s posrednim delovanjem sile je dana z enačbo:
Za istosmerno iztiskavanje valjčka je na primer posebej:
tako da je končni premer valjčka dan z rešitvijo:
kjer je:
pa začetni premer.
Medicina/nevroznanosti/psihologija[uredi | uredi kodo]
- Zgled 12
Lambertovo funkcijo W so uporabili na področju nevrološkega slikanja pri povezovanju možganskega pretoka krvi in sprememb porabe kisika med možganskimi voksli na ustreznem signalu nivoja krvne oksigenacije (BOLD).[4]
Posebne vrednosti[uredi | uredi kodo]
(konstanta Ω, (OEIS A030178))
Druge formule[uredi | uredi kodo]
Računski algoritem[uredi | uredi kodo]
Funkcijo W se lahko izračuna z rekurenčno enačbo:
ki so jo podali Corless idr. Naslednja Pythonova koda uporablja zgornjo zvezo in oceno računske napake, dano v delu Chapeau-Blondeauja in Monirja:
import math
def lambertW(x, prec = 1E-12, maxiters = 100):
w = 0
for i in range(maxiters):
we = w * math.exp(w)
w1e = (w + 1) * math.exp(w)
if prec > abs((x - we) / w1e):
return w
w -= (we - x) / (w1e - (w+2) * (we-x) / (2*w+2))
raise ValueError("W ne konvergira dovolj hitro za abs(z) = %f" % abs(x))
Program izračuna glavno vejišče za . lahko se izboljša z boljšimi začetnimi ocenami.
Če je potrebna manjša točnost, se lahko uporabi zaprta oblika približka v C, ali pa se lahko vzame kot odlična začetna ocena zgornjega programa, ki nato računa le z nekaj iteracijami:
double desy_lambert_W(double x) {
double lx1;
if (x <= 500.0) {
lx1 = ln(x + 1.0);
return 0.665 * (1 + 0.0195 * lx1) * lx1 + 0.04;
}
return ln(x - 4.0) - (1.0 - 1.0/ln(x)) * ln(ln(x));
}
(povzeto iz: http://www.desy.de/~t00fri/qcdins/texhtml/lambertw/)
Zgodovina[uredi | uredi kodo]
Lambertova funkcija W ima nenavadno zgodovino. Raziskovanje njenih značilnosti vodi do Eulerjevega članka iz leta 1779. Inverza wew, kot omembe vredne funkcije, niso raziskovali vse do 1980-ih. Razpoznanje je prišlo pri uporabi v računalniškem programu za simbolno računanje Maple, kjer so v ta namen uvedli rezervirano ime LambertW. Izbrali so Lambertovo ime, ker se je Euler v svojem članku skliceval na predhodno Lambertovo delo in morda zaradi tega, »ker poimenovanje še ene funkcije po Eulerju ne bi bilo uporabno« (Corless idr.).
Lambert je leta 1758 obravnaval rešitev enačbe:
sedaj znane kot Lambertova transcendentna enačba.[5] Euler je izvedel za Lambertov članek leta 1764. Leta 1783 je napisal članek o tej enačbi, kjer je obravnaval posebni primer z obliko:
ki je skoraj enaka definiciji funkcije , čeprav je predlagal definicijo funkcije v obliki .[6] Enačba ima rešitev:
Glej tudi[uredi | uredi kodo]
- Wrightova funkcija omega
- trinom (Lambertova trinomska funkcija)
- eksperimentalna matematika
- Jackiw-Teitelboimova gravitacija (model R=T)
Sklici[uredi | uredi kodo]
- ↑ Širca; Horvat (2010), §2.6.1, str. 87.
- ↑ Pudasaini (2011).
- ↑ Ohayon; Ron (2013).
- ↑ Sotero; Iturria-Medina (2011).
- ↑ Lambert (1758).
- ↑ Euler (1783).
Viri[uredi | uredi kodo]
- Euler, Leonhard (1783), »De serie Lambertina Plurimisque eius insignibus proprietatibus«, Acta Acad. Scient. Petropol. (2): 29–51 Ponatisnjeno v Euler, L., Opera Omnia, Series Prima, Vol. 6: Commentationes Algebraicae. Leipzig: Teubner, str. 350-369, 1921. (faksimile)
- Lambert, Johann Henrich (1758), »Observationes variae in mathesin puram« (PDF), Acta Helveticae physico-mathematico-anatomico-botanico-medica (Band III): 128–168
- Ohayon, B.; Ron, G. (2013), »New approaches in designing a Zeeman Slower«, Journal of Instrumentation, 8 (02): P02016, doi:10.1088/1748-0221/8/02/P02016
- Pudasaini, S. P. (2011), »Some exact solutions for debris and avalanche flows«, Physics of Fluids, 23 (4): 043301, doi:10.1063/1.3570532
- Sotero, Roberto C.; Iturria-Medina, Yasser (2011), »From Blood oxygenation level dependent (BOLD) signals to brain temperature maps«, Bulletin of Mathematical Biology, 73 (11): 2731–47, doi:10.1007/s11538-011-9645-5, PMID 21409512
- Širca, Simon; Horvat, Martin (2010), Računske metode za fizike, Matematika – fizika : zbirka univerzitetnih učbenikov in monografij, zv. 46 (1. izd.), DMFA – založništvo, COBISS 253114368, ISBN 978-961-212-227-0, ISSN 1408-1571
Zunanje povezave[uredi | uredi kodo]
- Corles idr., Zapiski o raziskovanju funkcije Lambert W (angleško)
- Corless idr., »On the Lambert W function« Adv. Computational Maths. 5, 329 - 359 (1996) (PDF)
- Scott, T.C.; Mann, R.B.; Martinez Ii, Roberto E. (2006). »General Relativity and Quantum Mechanics: Towards a Generalization of the Lambert W Function«. AAECC (Applicable Algebra in Engineering, Communication and Computing). Zv. 17, št. 1. str. 41–47. arXiv:math-ph/0607011. doi:10.1007/s00200-006-0196-1.
- Scott, T. C.; Fee, G.; Grotendorst, J. (2013). »Asymptotic series of Generalized Lambert W Function«. SIGSAM (ACM Special Interest Group in Symbolic and Algebraic Manipulation). Zv. 47, št. 185. str. 75–83.
- Scott, T. C.; Fee, G.; Grotendorst, J.; Zhang, W.Z. (2014). »Numerics of the Generalized Lambert W Function«. SIGSAM. Zv. 48, št. 1–2. str. 42–56.
- Maignan, Aude; Scott, T. C. (2016). »Fleshing out the Generalized Lambert W Function«. SIGSAM. Zv. 50, št. 2. str. 45–60. doi:10.1145/2992274.2992275.
- Chapeau-Blondeau, F. in Monir, A., »Evaluation of the Lambert W Function and Application to Generation of Generalized Gaussian Noise With Exponent 1/2«, IEEE Trans. Signal Processing, 50(9), 2002 Arhivirano 2012-03-28 na Wayback Machine.
- Weisstein, Eric Wolfgang. »Lambert W-Function«. MathWorld.
- Lambertova funkcija na Wolframovi strani funkcij. (angleško)
- Francis idr., »Quantitative General Theory for Periodic Breathing« Circulation 102 (18): 2214. (2000). Uporaba Lambertove funkcije pri reševanju časovno zakasnele dinamike v bolezni človeka.
- Extreme Mathematics. Monografije o Lambertovi funkciji W, njeni numerični aproksimaciji in posplošitvah za inverze W transcendentnih oblik s ponavljajočimi eksponetnimi stolpi. (angleško)
- Računanje Lambertove funkcije W Arhivirano 2008-01-30 na Wayback Machine. (angleško)
- Hayes, Brian, Zakaj W? (Why W?) Arhivirano 2008-04-07 na Wayback Machine. (angleško)






![{\displaystyle \int \operatorname {W} (x)\,\mathrm {d} x=x\left[\operatorname {W} (x)-1+{\frac {1}{\operatorname {W} (x)}}\right]+C\!\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19d5d9449652f4fc19645650efb92714ff9cd1dc)






















![{\displaystyle B_{n}\sim {\frac {1}{\sqrt {n}}}\left[{e^{\operatorname {W} (n)}}\right]^{n+{\frac {1}{2}}}e^{e^{\operatorname {W} (n)}-n-1}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf9ccfcb0bbf62fd5272c778c28f684467567d33)







![{\displaystyle h\nu =\left[3+\operatorname {W} \left({\frac {-3}{e^{3}}}\right)\right]k_{\rm {B}}T=2,8214393721\,k_{\rm {B}}T\!\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c0a08503b8ad09a2a87eee8ee8ac2fb04cf4f99)
![{\displaystyle {\frac {hc}{\lambda }}=\left[5+\operatorname {W} \left({\frac {-5}{e^{5}}}\right)\right]k_{\rm {B}}T=4,9651142317\,k_{\rm {B}}T\!\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f264cb6deef571a7234e3f8028dc2bab2a9b73b)
![{\displaystyle H(x)=1+\operatorname {W} \left[(H(0)-1)\exp((H(0)-1)-{\frac {x}{L}})\right]\!\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6502e90a73846d7680c34fd38b82bd8fa2ed6b3)




![{\displaystyle x=e^{\ln \left[4F\eta _{pr}/(\pi Cd_{0}^{2})\right]/n}\!\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16c6ad7b722cea30f740b3be75d52590c993fd0b)


















