1 + 2 + 3 + 4 + ···
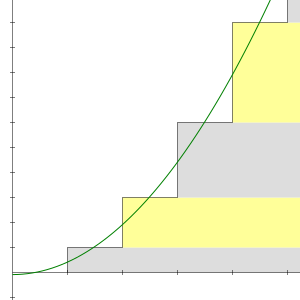
1 + 2 + 3 + 4 + ··· je v matematiki divergentna aritmetična vrsta. Predstavlja vsoto naravnih števil. Njena n-ta delna vsota je enaka trikotniškemu številu:
Ko se n približuje neskončnosti, vrsta narašča brez meja. Ker zaporedje delnih vsot ne konvergira h končni limiti, je vrsta divergentna in nima vsote v običajnem smislu.
Čeprav se zdi, da vrsta nima nobene pomembne vrednosti, se lahko obravnava na načine, ki vodijo do matematično zanimivih rezultatov, od katerih se nekateri rabijo na drugih področjih, kot so kompleksna analiza, kvantna teorija polja in teorija strun. V matematiki se rabi več sumacijskih metod za dodelitev številskih vrednosti tudi za divergentne vrste. Metodi regularizacije funkcije ζ in Ramanudžanove vsote posebej dodelita vsoti vrednost −1/12, kar se izraža v znameniti formuli:[1]
Sklici[uredi | uredi kodo]
Viri[uredi | uredi kodo]
- Lepowsky, J. (1999). »Vertex operator algebras and the zeta function«. V Naihuan Jing in Kailash C. Misra (ur.). Recent Developments in Quantum Affine Algebras and Related Topics. Contemporary Mathematics. Zv. 248. str. 327–340. arXiv:math/9909178.



