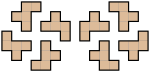
Pentomina

Vseh 18 enostranskih pentomin, vključno z zrcalnimi šestimi

Običajno označevanje pentomin z latiničnimi črkami. Včasih črko N nadomešča črka S.

Pentomína (tudi pentamína) je poliomina, ki jo sestavlja pet skladnih neprekrivajočih se enotskih kvadratov ortogonalno povezanih po stranicah. Beseda pentomina izhaja iz starogrške besede πέντε: pénte - pet in domina.

Obstaja 12 različnih prostih pentomin, ki se običajno označujejo s črkami latinične abecede, katerim so delno podobne. Praviloma pentomina, ki izhaja iz zrcaljenja ali zasuka poljubne pentomine, ne šteje za drugačen lik. Celotni množici pentomin rečemo tudi pentomino, oziroma pentamino. Naslednji liki:

niso pentomine, saj so vsaj enkrat povezani le z ogliščema. Takšni liki, imenovani nepentomine, skupaj s prostimi pentominami tvorijo množico likov, imenovanih (prosti) pentapleti. Pentapleti se pojavljajo v Conwayjevi igri življenja.

Pentomine F, L, N, P, Y in Z so hiralne v 2 razsežnostih. Če dodamo njihove zrcalne podobe (F', J, N', Q, Y', S), dobimo 18 enostranskih pentomin. Druge, označene z I, T, U, V, W in X, so enakovredne njihovim zavrtenim zrcalnim likom. To je pomembno v nekaterih računalniških igrah, kjer premiki zrcalnih podob niso dovoljeni, na primer v klonih Tetrisa in arkadni igri Rampart. Pentomine se poleg tetromin in drugih manjših likov pojavljajo v računalniški igri Pentix.

Z vsako od 12-tih pentomin lahko pokrivamo ravnino.

Conway je pentomine označeval drugače. Namesto I je pisal O, Q namesto L, R namesto F in S namesto N. Podobnost črkam je še bolj nenaravna (še posebej, ker je »O« raven lik, in ni podoben dejanski črki O). Prednost njegovega označevanja je v tem, da uporablja 12 zaporednih črk abecede. Ta shema se uporablja v povezavi z igro življenja, in tako govori o pentomini R namesto pentomine F.

Pri običajnem označevanju si lahko zapomnimo le zadnji del abecede (TUVWXYZ) in besedo FiLiPiNo. Velikokrat velja prepričanje, da je 5 tetromin premalo, 35 heksomin pa preveč, tako, da je 12 pentomin ravno prav.

Simetrija

12 prostih pentomin, pobarvanih glede na njihovo simetrijo

Če upoštevamo zasuke mnogokratnikov le pod kotom 90°, obstajajo naslednje simetrijske kategorije:

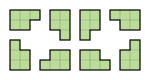
• pentomine F, L, N, P in Y nimajo simetrije. Lahko jih obrnemo na 8 načinov: 4 z zasukom in še 4 z zrcalnimi podobami. Njihovo simetrijsko grupo sestavlja le identična preslikava.
• pentomini T in U lahko obrnemo na 4 načine z zasukom. Njuna os zrcalne simetrije je poravnana z mrežnimi črtami. Njuna simetrijska grupa ima dva elementa, identiteto in zrcaljenje vzdolž črte vzporedne daljicam kvadratov.
• tudi pentomini V in W lahko obrnemo na 4 načine z zasukom. Njuna os zrcalne simetrije leži pod kotom 45° glede na mrežne črte. Njuna simetrijska grupa ima dva elementa: identiteto in diagonalno zrcaljenje.
• pentomino Z lahko obrnemo na 4 načine: 2 z zasukom in še 2 z njegovima zrcalnima podobama. Ima točkovno simetrijo, znano tudi kot rotacijska simetrija reda 2. Njegova simetrijska grupa ima dva elementa: identiteto in zasuk pod kotom 180°.
• pentomino I lahko obrnemo na 2 načina z zasukom. Ima dve osi zrcalne sismetrije, obe poravnani z mrežnimi črtami. Njegova simetrijska grupa ima štiri elemente: identiteto, dve zrcaljenji in zasuk pod kotom 180°. To je diedrska grupa reda 2, znana tudi kot Kleinova štirikratna grupa.
• pentomino X lahko obrnemo le na en način. Ima štiri osi zrcalne simetrije, poravnane z mrežnimi črtami in diagonalami, ter rotacijsko sismetrijo reda 4. Njegova simetrijska grupa, diedrska grupa reda 4, ima osem elementov.

Če ločujemo zrcaljenja pentomin, kot pri enostranskih pentominah, sta prva in četrta kategorija dvakrat večji, kjer dobimo dodatnih 6 pentomin od skupnih 18. Če ločujemo tudi zasuke, potem moramo pentomine v prvi kategoriji šteti osemkrat, pentomine v naslednjih treh kategorijah (T, U, V, W, Z) štirikrat, pentomino I dvakrat in X le enkrat. Tako dobimo 5 · 8 + 5 · 4 + 2 + 1 = 63 negibnih pentomin.

Naslednje slike prikazujejo osem različnih obrnitev pentomin F, L, N, P in Y:

  

Za dvorazsežne like sta v splošnem še dve kategoriji:

• lahko jih obrnemo na 2 načina z zasukom pod kotom 90°, z dvema osema zrcalne simetrije, obema poravnanima z diagonalami. Takšna vrsta simetrije zahteva vsaj heptomino.
• lahko jih obrnemo na 2 načina, kot sami sebi zrcalni podobi, na primer svastika. To je rotacijska simetrija reda 4. Ta vrsta simetrije zahteva vsaj oktomino.

Pokrivanje pravokotnikov in kvadratov

S pentominami je povezanih veliko ugank in problemov. Standardna pentominska uganka je pokrivanje pravokotnika s pentominom, tako da se pentomine ne prekrivajo med seboj in da v pravokotniku ni praznih mest. Vsaka od 12-tih pentomin ima površino 5 enot, tako da mora imeti pravokotnik površino 60 enot. Možne velikosti so 6 × 10, 5 × 12, 4 × 15 in 3 × 20. Spretni reševalci lahko verjetno rešijo te probleme na roko v nekaj urah. Bolj zapletena naloga, ki običajno zahteva računalniško iskanje, pa je štetje skupnega števila rešitev za vsak primer.

Primer 6 × 10 sta prva rešila leta 1960 Colin Haselgrove in Jenifer Haselgrove. Obstaja točno 2339 rešitev, brez trivialnih različic, ki jih dobimo z zasukom ali zrcaljenjem celega pravokotnika, in z upoštevanjem zasuka in zrcaljenja podmnožice pentomin (kar nam včasih da dodatno rešitev na preprost način).

Primer 5 × 12 ima 1010 rešitev, 4 × 15 ima 368 rešitev, 3 × 20 pa le 2 rešitvi (ena je prikazana na sliki, drugo lahko dobimo, če zasučemo cel blok, ki vsebuje pentomine L, N, F, T, W, Y in Z).

Malo lažjo (bolj simetrično) uganko, pokritje kvadrata 8 × 8 z luknjo 2 × 2 v sredini, je rešil Scott leta 1958. Obstaja 65 rešitev. Scottov algoritem je eden prvih uporab programa z vračanjem. Zgled vseh devetnajstih pokritij kvadrata 8 × 8, kjer je pentomina X na mestu:

V različicah te uganke se lahko luknje postavijo poljubno. Veliko takšnih vzorcev je rešljivih, z izjemo, da se vsak par lukenj ne sme postaviti blizu kota kvadrata, tako da lahko kot zasede le pentomina P, ali da v kot postavimo pentomini T ali U, kjer nastane nova luknja.

Za reševanje takšnih problemov so opisali učinkovite algoritme, na primer Knuth. Če jih poženemo na sodobni računalniški opremi, lahko te pentominske uganke rešimo v nekaj sekundah.

Zgled dveh pokritij kvadrata 11 × 11 s štirimi luknjami 2 × 2 z »vzporedno polarizirano« množico 21-tih pentomin

Pentomine v književnosti

Pentomine, še posebej rešitev pravokotnika 3 × 20 ([UXPI][LNFTWYZ]V), je v svojem znanstvenofantastičnem romanu Imperial Earth, objavljenem leta 1975, predstavil Clarke. Upal je tudi, da bodo predstavljene tudi v filmu 2001: Vesoljska odiseja, vendar je prevladal šah. V svojem otroškem romanu Chasing Vermeer iz leta 2003, ki ga je ilustriral Helquist, jih je predstavila tudi Balliettijeva. Prav tako v nadaljevanjih romana, The Wright 3 in The Calder Game.

Glej tudi

• Lonpos

Viri

• Batagelj, Vladimir (1974). "Pentomino". Presek 2 (1): str. 40-42. (COBISS). http://www.presek.si/2/2-1-Batagelj.pdf. 
• Golomb, Solomon Wolf (1996). Polyominoes: puzzles, patterns, problems, and packings. Princeton University Press. ISBN 0-691-08573-0. http://books.google.com/books?id=sbQj2dILLIsC&printsec=frontcover&hl=sl&source=gbs_ge_summary_r&cad=0#v=onepage&q&f=false. 
• Haselgrove, Colin Brian; Haselgrove, Jenifer (oktober 1960). "A Computer Program for Pentominoes". Eureka 23: 16–18. 
• Martin, George Edward (1991). Polyominoes: a guide to puzzles and problems in tiling. Cambridge University Press. ISBN 0-88385-501-1. http://books.google.com/books?id=D8KbnTGXDWEC&printsec=frontcover&hl=sl&source=gbs_ge_summary_r&cad=0#v=onepage&q&f=false. 
• Potočnik, Aleksander (2002). "Polinomine". Brihtnež 0 (1): str. 4-7. http://www.dmfa.si/Brihtnez/BrihtnezIndex.html. 
• Scott, Dana Stewart (1958). "Programming a combinatorial puzzle". Technical Report No. 1 (Oddelek za elektrotehniko, Univerza Princeton). 

Zunanje povezave

• Pentomino na MathWorld (v angleščini)
• Gerard's Pentomino Page (v angleščini)