Splošna normalna porazdelitev

Splošna normalna porazdelitev (1. oblika)
Funkcija gostote verjetnosti za splošno normalno porazdelitev 1. oblike
Zbirna funcija verjetnosti za splošno normalno porazdelitev 1. oblike.
oznaka
parametri	$\mu \,$ parameter lokacije (realno število) $\alpha \,$ parameter merila (pozitiven) $\beta \,$ parameter oblike (pozitiven)
interval	$x \in (-\infty; +\infty)\!$
funkcija gostote verjetnosti (pdf)	$\frac{\beta}{2\alpha\Gamma(1/\beta)} \; e^{-(|x-\mu|/\alpha)^\beta}$ $\Gamma \!$ označuje funkcijo gama
zbirna funkcija verjetnosti (cdf)	$\frac{1}{2} + \sgn(x-\mu)\frac{\gamma\left(1/\beta, \left( \frac{|x-\mu|}{\alpha} \right)^\beta\right)}{2\Gamma(1/\beta)}$ $\gamma \!$ pomeni spodnjo nepopolno funkcijo gama
pričakovana vrednost	$\mu \,$
mediana	$\mu \,$
modus	$\mu \,$
varianca	$\frac{\alpha^2\Gamma(3/\beta)}{\Gamma(1/\beta)}$
simetrija	$0 \!$
sploščenost	$\frac{\Gamma(5/\beta)\Gamma(1/\beta)}{\Gamma(3/\beta)^2}-3$
entropija	$\frac{1}{\beta}-\log\left[\frac{\beta}{2\alpha\Gamma(1/\beta)}\right]$
funkcija generiranja momentov (mgf)
karakteristična funkcija

Splošna normalna porazdelitev (tudi splošna Gaussova porazdelitev) je katerakoli porazdelitev izmed dveh zveznih verjetnostnih porazdelitev, ki se od normalne porazdelitve razlikujta v tem, da vsebujeta še parameter oblike (normalna porazdelitev ga ne vsebuje). Splošna normalna porazdelitev nastopa v dveh oblikah, ki ju označujemo kot 1. oblika in 2. oblika

Lastnosti porazdelitve splošne normalne porazdelitve 1. oblike

Splošna normalna porazdelitev 1. oblike je znana tudi kot potenčna porazdelitev ali splošna porazdelitev napak. Vključuje vse oblike normalne porazdelitve in Laplaceovih porazdelitev. Kot skrajni primer pa vključuje tudi vse zvezne enakomerne porazdelitve.

Funkcija gostote verjetnosti

Funkcija gostote verjetnosti za splošno normalno porazdelitev 1. oblike je

$\frac{\beta}{2\alpha\Gamma(1/\beta)} \; e^{-(|x-\mu|/\alpha)^\beta}$

$\Gamma$

kjer je

• $\Gamma(1/\beta) \!$ funkcija gama

Zbirna funkcija verjetnosti

Zbirna funkcija verjetnosti je enaka

$\frac{1}{2} + \sgn(x-\mu)\frac{\gamma\left(1/\beta, \left( \frac{|x-\mu|}{\alpha} \right)^\beta\right)}{2\Gamma(1/\beta)}$

kjer je

• $\gamma \!$ spodnja nepopolna gama funkcija

Pričakovana vrednost

Pričakovana vrednost je

$\mu \,$.

Varianca

Varianca je

$\frac{\alpha^2\Gamma(3/\beta)}{\Gamma(1/\beta)}$.

kjer je

• $\Gamma(x) \!$ funkcija gama

Sploščenost

Sploščenost je enaka

$\frac{\Gamma(5/\beta)\Gamma(1/\beta)}{\Gamma(3/\beta)^2}-3$

kjer je

• $\Gamma(x) \!$ funkcija gama

Povezave z drugimi porazdelitvami

• Kadar je $\beta = 2 \!$, dobimo normalno porazdelitev.
• Kadar pa je $\beta = 1 \!$, dobimo Laplaceovo porazdelitev
• Kadar pa velja $\beta \to \infty \!$, dobimo zvezno enakomerno porazdelitev na intervalu $(\mu - \alpha, \mu + \alpha) \!$

Lastnosti splošne normalne porazdelitve 2. oblike

Splošna normalna porazdelitev (2. oblika)
Funkcija gostote verjetnosti za splošno normalno porazdelitev 2. oblike
Zbirna funcija verjetnosti za splošno normalno porazdelitev 2. oblike.
oznaka
parametri	$\xi \!$ parameter lokacije (realno število) $\alpha \,$ parameter merila (pozitivno realno število) $\kappa \,$ parameter oblike (realno število)
interval	$x \in (-\infty,\xi+\alpha/\kappa) \text{ kadar je } \kappa>0$ $x \in (-\infty,\infty) \text{ kadar je } \kappa=0$ $x \in (\xi+\alpha/\kappa; +\infty) \text{ kadar je } \kappa<0$
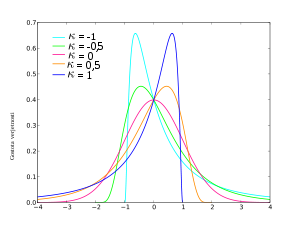
funkcija gostote verjetnosti (pdf)	$\frac{\Phi(y)}{\alpha-\kappa(x-\xi)}$, kjer je $y = \begin{cases} - \frac{1}{\kappa} \log \left[ 1- \frac{\kappa(x-\xi)}{\alpha} \right] & \text{ kadar je } \kappa \neq 0 \\ \frac{x-\xi}{\alpha} & \text{ kadar je } \kappa=0 \end{cases}$ $\Phi \!$ je standardna funkcija gostote verjetnosti za normalno porazdelitev
zbirna funkcija verjetnosti (cdf)	$\Phi(y) \!$, kjer je $y = \begin{cases} - \frac{1}{\kappa} \log \left[ 1- \frac{\kappa(x-\xi)}{\alpha} \right] & \text{ kadar je } \kappa \neq 0 \\ \frac{x-\xi}{\alpha} & \text{ kadar je } \kappa=0 \end{cases}$ $\Phi \!$ je standardna zbirna funkcija verjetnosti za normalno porazdelitev
pričakovana vrednost	$\xi - \frac{\alpha}{\kappa} \left( e^{\kappa^2/2} - 1 \right)$
mediana	$\xi \,$
modus
varianca	$\frac{\alpha^2}{\kappa^2} e^{\kappa^2} \left( e^{\kappa^2} - 1 \right)$
simetrija	$\frac{3 e^{\kappa^2} - e^{3 \kappa^2} - 2}{(e^{\kappa^2} - 1)^{3/2}} \text{ sign}(\kappa)$
sploščenost	$e^{4 \kappa^2} + 2 e^{3 \kappa^2} + 3 e^{2 \kappa^2} - 6$
entropija
funkcija generiranja momentov (mgf)
karakteristična funkcija

Funkcija gostote verjetnosti

Funkcija gostote verjetnosti za splošno normalno porazdelitev 1. oblike je

$\frac{\phi(y)}{\alpha-\kappa(x-\xi)}$, kjer je
$y = \begin{cases} - \frac{1}{\kappa} \log \left[ 1- \frac{\kappa(x-\xi)}{\alpha} \right] & \text{ kadar je } \kappa \neq 0 \\ \frac{x-\xi}{\alpha} & \text{ kadar je } \kappa=0 \end{cases}$
$\phi \!$ je standardna funkcija gostote verjetnosti za normalno porazdelitev

Zbirna funkcija verjetnosti

Zbirna funkcija verjetnosti je enaka

$\Phi(y) \!$, kjer je
$y = \begin{cases} - \frac{1}{\kappa} \log \left[ 1- \frac{\kappa(x-\xi)}{\alpha} \right] & \text{ kadar je } \kappa \neq 0 \\ \frac{x-\xi}{\alpha} & \text{ kadar je } \kappa=0 \end{cases}$
$\Phi \!$ je standardna zbirna funkcija verjetnosti za normalno porazdelitev

Pričakovana vrednost

Pričakovana vrednost je

$\xi - \frac{\alpha}{\kappa} \left( e^{\kappa^2/2} - 1 \right)$.

Varianca

Varianca je

$\frac{\alpha^2}{\kappa^2} e^{\kappa^2} \left( e^{\kappa^2} - 1 \right)$

Sploščenost

Sploščenost je enaka

$e^{4 \kappa^2} + 2 e^{3 \kappa^2} + 3 e^{2 \kappa^2} - 6$

Glej tudi

• seznam verjetnostnih porazdelitev