Laplaceova porazdelitev

Laplaceova porazdelitev
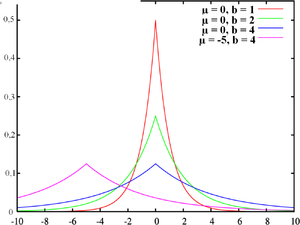
Funkcija gostote verjetnosti za Laplaceovo porazdelitev
Zbirna funcija za Laplaceovo porazdelitev.
oznaka	$Laplace(\mu ,b)\!$
parametri	$\mu \,$ parameter lokacije (realno število) $b>0\,$ parameter merila (realno število)
interval	$x\in (-\infty ;+\infty )\,$
funkcija gostote verjetnosti (pdf)	${\frac {1}{2\,b}}\exp \left(-{\frac {\|x-\mu \|}{b}}\right)\,$
zbirna funkcija verjetnosti (cdf)	glej opis lastnoti
pričakovana vrednost	$\mu \,$
mediana	$\mu \,$
modus	$\mu \,$
varianca	$2\,b^{2}$
simetrija	$0\,$
sploščenost	$3\,$
entropija	$\log(2\,e\,b)$
funkcija generiranja momentov (mgf)	${\frac {\exp(\mu \,t)}{1-b^{2}\,t^{2}}}\,\!$ za $\|t\|<1/b\,$
karakteristična funkcija	${\frac {\exp(\mu \,i\,t)}{1+b^{2}\,t^{2}}}\,\!$

Laplaceova porazdelitev [laplásova ~] je družina zveznih verjetnostnih porazdelitev, ki je določena z dvema parametroma. Včasih jo imenujejo tudi dvojna eksponentna porazdelitev, ker je ta porazdelitev pravzaprav razlika med dvema eksponentnima porazdelitvama.

Imenuje se po francoskem matematiku in astronomu Pierre-Simonu de Laplaceu (1749 – 1827).

Lastnosti

Funkcija gostote verjetnosti

Funkcija gostote verjetnosti za porazdelitev je

f(x|\mu ,b)={\frac {1}{2b}}\exp \left(-{\frac {|x-\mu |}{b}}\right)\,\!

to je

={\frac {1}{2b}}\left\{{\begin{matrix}\exp \left(-{\frac {\mu -x}{b}}\right)&{\mbox{če je }}x<\mu \\[8pt]\exp \left(-{\frac {x-\mu }{b}}\right)&{\mbox{če je }}x\geq \mu \end{matrix}}\right.

Zbirna funkcija verjetnosti

Zbirna funkcija verjetnosti je enaka

F(x)\,=\int _{-\infty }^{x}\!\!f(u)\,\mathrm {d} u

to je

=\left\{{\begin{matrix}&{\frac {1}{2}}\exp \left({\frac {x-\mu }{b}}\right)&{\mbox{če je }}x<\mu \\[8pt]1-\!\!\!\!&{\frac {1}{2}}\exp \left(-{\frac {x-\mu }{b}}\right)&{\mbox{če je }}x\geq \mu \end{matrix}}\right.

ali

0,5\,[1+\operatorname {sgn}(x-\mu )\,(1-\exp(-|x-\mu |/b))].

Pričakovana vrednost

Pričakovana vrednost je enaka

\mu \,

.

Varianca

Varianca je enaka

2\,b^{2}

.

Funkcija generiranja momentov

Funkcija generiranja momentov je

{\frac {\exp(\mu \,t)}{1-b^{2}\,t^{2}}}\,\!

za

|t|<1/b\,

.

Karakteristična funkcija

Karakteristična funkcija je

{\frac {\exp(\mu \,i\,t)}{1+b^{2}\,t^{2}}}\,\!

.

Povezave z drugimi porazdelitvami

Če ima slučajna spremenljivka $X\!$ Laplaceovo porazdelitev $X\sim \mathrm {Laplace} (0,b)\,$ , potem ima spremenljivka $|X|\!$ eksponentno porazdelitev, kar zapišemo takole $|X|\sim \mathrm {Exp} (b^{-1})\,$ .

Če ima slučajna spremenljivka $X\!$ eksponentno pozazdelitev $X\sim \mathrm {Exp} (\lambda )\,$ in ima od $X\!$ neodvisna slučajna spremenljivka $Y\!$ Bernoullijevo porazdelitev ${Y\sim \,}$ $\mathrm {Bernoulli} (0,5)\,$ , potem ima $X(2Y-1)\!$ Laplaceovo porazdelitev $X(2Y-1)\sim \mathrm {Laplace} (0,\lambda ^{-1})\,$ .

Če imamo dve slučajni spremenljivki, ki imata eksponentno porazdelitev $X_{1}\sim \mathrm {Exp} (\lambda _{1})\,$ in $X_{2}\sim \mathrm {Exp} (\lambda _{2})\,$ in je $X_{2}\!$ neodvisna od $X_{1}\,$ , potem ima slučajna spremenljivka $\lambda _{1}X_{1}-\lambda \!$ Laplaceovo porazdelitev $\lambda _{1}X_{1}-\lambda _{2}X_{2}\sim \mathrm {Laplace} \left(0,1\right)\,$ .

Če ima slučajna spremenljivka $V\!$ eksponentno porazdelitev $V\sim \mathrm {Exp} (1)\,$ in ima od $V\!$ neodvisna slučajna spremenljivka $Z\!$ normalno porazdelitev $Z\sim \mathrm {N} (0,1)\,$ , potem ima slučajna spremenljivka $X=\mu +b{\sqrt {2V}}Z\!$ Lapleceovo porazdelitev $X\sim \mathrm {Laplace} (\mu ,b)\!$ .

Splošna Gaussova porazdelitev (1. oblike) je enaka Laplaceovi porazdelitvi, če njen parameter oblike postavimo na 1. Parameter merila $\alpha \!$ je potem enak $b\!$ .

Zunanje povezave

Laplaceova porazdelitev na MathWorld (angleško)
Opis Lapleceove porazdelitve na Xycoon (angleško)

Glej tudi